物流配送中心选址的重心法探讨

程 珩 牟瑞芳

西南交通大学，交通运输与物流学院，成都 610031

0 引 言

重心法作为单一设施选址问题中最基本的方法之一，使用较为频繁，在物流选址的教科书上都可以找到，但课本中对于重心法的来龙去脉，都没有做详细的探讨，也没有把重心法和微分法的关系清楚解释，在最后的迭代过程中亦存在不足之处。因此，有必要对重心法做深入的讨论。

鲁晓春等指出了重心法存在的不足，即重心法求出的重心坐标不是最佳配送中心值，并提出用微分法代替重心法[1]。苗兴东等对于重心法最后迭代过程中总运输费用的变化规律以及总费用发生突变时两点间距离的变化做了具体的分析，并提出了函数不均匀性这一概念[2]。但是，两篇论文中没有对重心法是如何引入，以及求偏导数的具体过程做详细分析。

本文根据单一设施选址问题中配送中心到各个需求点的总运输费用最少这一目标，按照求最值问题的数学方法对该问题求解，利用数学归纳法，推导了物流配送中心坐标的计算公式。由于该计算公式中等式左边右边都有未知数，无法直接求出最终解，对此引入重心法，最后对以往的迭代方案提出了自己的新看法。

1 模型的建立

按照设施数量划分，选址问题可以分为单一设施选址和多设施选址。单一设施选址与同时对多个设施选址是截然不同的两个问题。单一设施选址无需考虑竞争力、设施之间的需求分配、集中库存的效果、设施成本与数量之间的关系等，而运输成本是要考虑的首要因素。

解决单一设施选址问题的模型有四种：（1）微分法——重心法；（2）交叉中值模型；（3）因素评价法；（4）层次分析模型。

1.1 单一设施选址的目标

跟多设施选址问题相比，单一设施选址是比较简单的一类，所选择的配送中心应该位于可使运输费用最小的地方。所以，选择一个合适的配送中心，使得从该配送中心到各个需求点的总运输费用最少是单一设施选址问题的最终目标。

1.2 重心法的三个基本假设

重心法模型是选址问题中最常用的一种模型，可以用来解决连续区域直线距离的单点选址问题。利用重心法进行选址时，有三个基本假设，即：

（a）运输费用只与配送中心和需求点的直线距离有关，不考虑城市交通状况；（b）不考虑配送中心所处地理位置的地产价格；（c）各个需求点的位置和需求量已知而且不变。

1.3 建立模型

建立模型的依据是：单一设施选址的目标为配送中心到各个需求点的总运输费用最少。

假设在一个计划区域内，有n个需求点，各点

由于在物流配送中心选址时，应该保证总运输费用最少，即H最小，也就要求 (,)pxy中x，y为何值时使得总费用H最小，所以，这个问题就转化为求最值问题。根据高等数学中求最值得原理，显然让目标函数值H分别对 x，y求偏导数，令其偏导数分别等于零，求出x，y的值，即物流配送中心最佳位置的坐标。

1.4 求偏导数

由于该函数比较复杂，直接求偏导数难度大，而且又很费时，所以应该化繁为简，采用数学归纳法对其进行求解。计算过程如下：

（a）当 1i=时，原式

H对x求偏导数：

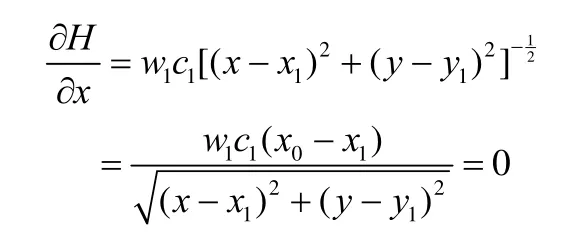
得出

同理可以得出

（b）当 2i= 时，原式

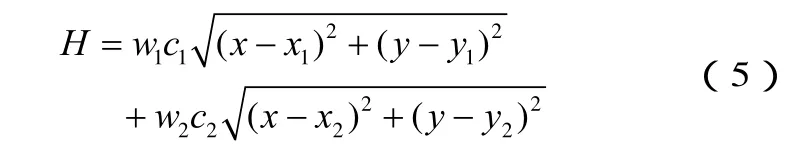
H对x求偏导数：

同理可得：

2 重心法的引入

由于在H对x，y分别求偏导数所得出来最终结果当中，等式左边和右边都有未知数x，y，所以，单独使用此方法计算不出来最终的结果，如果要将式中右端的x，y完全消除，计算起来十分复杂，为此，我们一般采用迭代法来求解。

迭代法求解必须要首先给出一个初始解，为了避免给出初始值盲目性，我们通常采取两种方法，一种是将坐标平面上原点的坐标（0，0）点带入来求解，第二种是引入重心法，通常是由重心法求的系统的重心坐标，以重心坐标作为初始解。

2.1 重心法的概念

重心法是一种模拟方法，它将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统，各点的需求量和资源量分别看成是物体的重量，系统的重心作为物流网点的最佳设置点，利用求物体系统重心的方法来确定物流网点的位置。

2.2 如何确定需求点的坐标

重心法首先要在坐标系中标出各个地点的位置，目的在于确定各点的相对距离。坐标系可以随便建立。在国际上的选址中，经常采用经度和纬度建立坐标，然后，根据各点在坐标系中的横纵坐标值求出重心点的最佳位置坐标x和y。

2.3 重心法的推导过程

原理：力和力臂的乘积等于力对转轴的力矩。即M FL= 。

按照重心法，将各需求点和资源点都视为有重量的质点，需求点的等效重量为根据重心的定义，资源点的等效重量为G，这样，寻求物流配送中心地址问题转化为求重心坐标的问题。

根据重心的特性可知，资源点的等效重量在重心处对原点在oxy平面产生的力矩等于各需求点对原点在oxy平面产生的力矩之和，可表示为：

式中，0d表示资源点到原点的距离。

将力矩沿x轴，y轴分解，重心点（资源点）对x轴、y轴产生的力矩等于各质点（需求点）对x轴、y轴产生的力矩之和，可表示为:

最终得到重心的坐标为：

由上式得到的重心位置的坐标点(,)xy，即所要求的初始解。

3 迭代的过程和最优方案的确定

迭代方案1[3]：

（a）以所有需求点的中心坐标作为配送中心的

（e）将 H1与 H0进行比较，若 H1< H0，则返回步骤c再次将代入公式（9）和公式（10）进行计算，计算配送中心的再改善地点如果,则说明就是最优解。

迭代方案2：

将初始坐标(,)xy带入公式（9）和公式（10）进行计算，计算出改进方案以此类推，反复迭代，直到两次迭代结果相同（或无限接近）时为止，这时候得到极小值点，即最优方案。

两种迭代方案的比较：

第一种迭代方案中只是将每一步迭代后的运费跟前一次的运费进行比较，只要迭代后所得的运费比前一次的运费大时就停止迭代，选择前一次计算出来的x和y的值最为最终解，但存在着局限性，因为该方案并没有计算到最后把极值点找出来。因此，所得到的解很有可能只是局部最优解，而不是整体最优解。

第二种迭代方案则一直迭代下去，直到迭代后和迭代前的值相等（或无限接近）为止，这时候没办法在进行进一步迭代，便找到了极值点。因为在迭代时只出现一个极值点，而且没有不可导的点，所以，这个极值点所对应的运输费用最少，该极值点就是物流配送中心的最佳位置的坐标。

两种方案各有利弊，一般情况下，我们要计算物流配送中心的位置，由于最终还要受客观条件的限制，不需要过于精确，只需找到一个相对比较合适的位置即可，在这种情况下，采用第一种迭代方案，计算量相对而言比较少，容易较快的得到结果。如果要特别精确的话，采用第一种迭代方案显然不可行，必须采用第二种迭代方案计算出最优解，但是，这个过程毫无疑问计算量很大，会给操作人员带来很大的不便，必须采用相关软件进行计算。

4 重心法选址方案的优缺点

优点：按运输费用最小原则来选址，并且对候选位置不加限制，因此具有较大的灵活性。

缺点：首先，由于灵活性较大，计算出来的最佳选址点可能受实际地理状态（如高山或河流、湖泊等）限制，而不易修建配送中心。因此，决策者考虑这些因素后有时不得不放弃这一最优解的位置，而选择选择现实当中可行的满意方案。

此外，上述计算的距离均为直线距离，这在实际问题当中往往也不大可行。在实际距离不是直线距离的条件下，可在运输费率中加以修正，使之适当增大，以补偿在计算直线距离时所产生的偏差。

最后，这种方法迭代次数较多，计算工作量比较大，计算成本也比较高。

5 结束语

本文对重心法的引入问题、利用数学归纳法对微分法求偏导数的过程做了详尽的阐述，对以往的迭代方案做了相应的补充和改进，并对这两种方案的优缺点进行了比较。然而，对于重心法中最后的迭代方案只是做了理论探讨，并没有给出具体的例子来很好的论证，对于这一问题，有待进一步去研究、去完善。

[1] 鲁晓春，詹荷生．关于配送中心重心法选址的研究[J]．北方交通大学学报，2000，24（6）:108-110.

[2] 苗兴东，李映红，范存军．重心法选址探讨[J]．交通标准化，2004，134: 50-52.

[3] 赵家俊．现代物流配送管理[M]．北京：北京大学出版社，2004．