不同交通流运行状态下的行程时间可靠性分析

李晓莉

天津市市政工程研究院，天津 300074

0 引 言

可靠性是指系统或单元在规定的条件下和规定的期限内完成预定功能的能力，可以用来评价复杂系统的鲁棒性。交通系统作为由人、车、路和环境组成的复杂系统，交通需求和供给因受各种因素的影响而处于不断变化的状态，这使得交通系统的可靠性经受到考验。行程时间可靠性是衡量道路可靠性的最直观指标，也是出行者出行最为关心的指标。随着城市交通需求激增，交通拥堵的普遍化和扩大化，居民出行难、出行时间无法保障的现象日益突出，使得行程时间可靠性成为学者们研究的热点问题。

行程时间可靠性是指在一定的服务水平下，出行者在规定的时间内完成出行的概率[1]。我国许多学者通过拟合行程时间分布函数，规定行程时间阈值，建立可靠度模型，研究了道路的行程时间可靠性[2-5]，但是，由于不同学者采用的统计时窗不一致，导致行程时间的分布函数不一致，且对行程时间阈值的选取方法没有深入研究，使得行程时间可靠性随阈值的改变而发生较大变化。其他学者或研究机构提出了衡量行程时间可靠性的其他指标，如计划行程时间指数、行程时间指数、预留时间指数、延迟时间指数等[6-8]。经过比较发现，这些指标之间存在较大的差异，是从不同的侧面反映交通流的运行状态。笔者认为行程时间可靠性不应是一个单一内涵的概念，它应既能体现出道路运输的时间效率又能体现出运输时间的稳定性，这样才能全面评价道路的可靠性。

本文以车牌识别数据为依托，以路径单元为研究对象，分析行程时间可靠性在全天的分布情况。首先给出行程时间可靠性更为直观、合理的内涵，其次对现有常用可靠性指标进行分类，而后对交通流运行状态进行简单划分，讨论在不同的交通流运行状态下两类指标的变化情况，也即行程时间可靠性的变化情况。本文的研究成果便于交通管理者和出行者准确把握交通流运行状况，为其行为决策提供依据。

1 相关定义

1.1 路径单元定义

目前，我国一些大城市的交通系统中安装了一定密度的车牌识别设备，可以长期、实时、稳定地记录经过车辆的车牌号、经过时间、运行方向、行驶位置等信息，经牌照配对可方便地获取行程时间样本数据[9]，经异常值处理可以得到较为准确的行程时间，为行程时间可靠性的研究提供了数据支持。

将沿同一运行方向，相邻两套识别设备之间的交通实体称为一个路径单元，作为本文研究的最小道路单位。路径单元是道路网的组成部分，以路径单元为研究对象，一方面可以大致反映路网的运行情况，另一方面可以便于管理者找到具体的交通瓶颈所在，为其采取交通管理措施提供依据，同时也便于出行者绕开交通拥堵路段。

图1为典型的车牌识别设备的安装示意图，其中A0、B0之间的道路实体为一个路径单元，A2、B2之间的道路实体为相反方向的路径单元。

图1 路径单元示意Fig.1 Schematic diagram of the path unit

1.2 出发时段定义

交通流的运行状态随时间动态变化，要分析交通流在一天的变化情况，需将一天24h划分成多个出发时段。根据本文采用数据的特点，10分钟的统计间隔既可以保证样本数据量，又便于细致分析交通流在全天的变化情况。因此，本文以每 10 min作为一个出发时段。此外，行程时间可靠性是衡量交通系统长期运行状态的指标，某一路径单位的行程时间可靠性的高低，是对一定时期内该路径单元交通流运行状态的综合反映。本文的研究依据某城市路网中一个月内的车牌识别数据，计算一个月内不同出发时段在该路径单元出发的车辆的行程时间，作为该路径单元的行程时间样本数据。

1.3 行程时间可靠性定义

行程时间可靠性是评价道路可靠性的一个指标，因此，行程时间可靠性的定义应能满足评价道路可靠性的要求。笔者认为道路可靠性应具备两个层面的内涵，首先是效率层面的可靠性，因为道路的功能是实现运输，交通只是人们生活和生产的衍生需求，交通花费的时间越少由交通产生的负效益越低，因此，道路的可靠性首先应体现在尽可能低的交通延误，即道路尽可能发挥其最大的运输时间效率，称之为道路功能的发挥程度；其次是稳定性层面的可靠性，一方面由于人们规律性的交通出行，日与日之间的交通流具有一定的相似性，而另一方面由于交通需求和供给的随机波动，不同日期同一时段内的行程时间会有所波动，这种波动性，使得人们对行程时间的可依赖程度降低，因此，行程时间的可靠性还应能体现人们在同一时段出行时对行程时间的可依赖程度，称之为道路功能发挥的稳定程度。因此，从行程时间可靠性的应用角度出发，将行程时间可靠性定义为能反映道路功能发挥程度以及道路功能发挥稳定程度的指标集。

2 行程时间可靠性指标分析

2.1 行程时间可靠性指标[6-8]

目前，衡量行程时间可靠性的常用指标有计划行程时间指数指标、行程时间指数指标、预留时间指数指标和延迟时间指数指标。

（1）计划行程时间指数（Planning travel time index,PPTI ）

计划行程时间指数是指为保证一定的到达概率（95%），出行者所需的行程时间与自由流条件下行程时间的比值，即：

（2）行程时间指数（Travel time index，TTI）

行程时间指数是指某一出发时段内，所有出行的行程时间均值与自由流条件下行程时间的比值，即：

（3）预留时间指数（Buffer time index，BTI ）预留时间指数是指为保证一定的到达概率的95%，出行者需要额外准备的行程时间与该时段出行时间均值的比值。

（4）延迟时间指数（Latest arrival travel time index，LATI ）

延迟时间指在多次出行中，出行者遭遇较大延误时（一般采用最晚到达的20%的出行经历）所需的行程时间均值与其总体出行时间均值的差值，延迟时间指数即是指延迟时间与出行时间均值的比值，即：

2.2 指标间关系分析

图2为路径单元1不同行程时间可靠性指标在全天的分布情况。可以看出，PPTI 与TTI 、BTI 与LATI之间分别具有相似的变化趋势，PPTI 、TTI 与BTI 、LATI之间变化趋势差异较大，某些时段变化趋势相反。

图2 不同出发时段行程时间可靠性分布Fig.2 Distribution of travel time reliability in different departure time windows

为进一步了解各指标之间的关系，选取若干段快速路路径单元作为研究对象，计算每条路径单元每个出发时段行程时间可靠性的指标值，采用SPSS软件进行指标间相关性分析。为了使不同路径单元及各指标间的指标值具有可比性，采用最小-最大方法将行程时间可靠性指标值规范化到[0-1]之间，分析结果如表1所示。

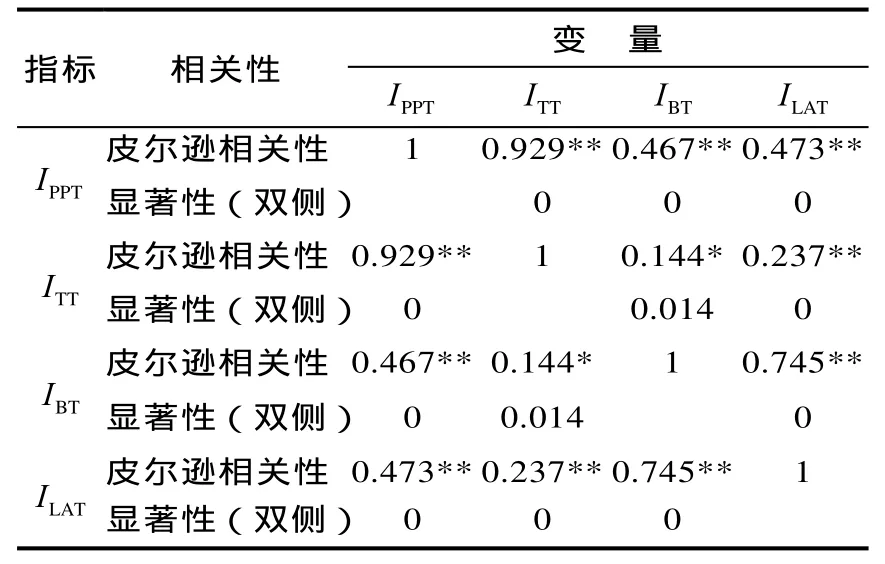
表1 行程时间可靠性指标相关性分析Tab.1 Correlation analysis of travel time reliability index

由表 1数据及变量间的相关性分级[10]可知，与 ITT、 IBT与 ILAT之间具有高度线性相关性，它们之间的相关性远远高于其他指标之间的相关性，而TTI 与LATI 之间仅具有低度相关性。分析原因如下：计划行程时间指数和行程时间指数计算的基准值是自由流条件下的行程时间，因而更多地反映了交通系统的运行效率。该指标值较高时，说明道路的运行效率较差，交通拥堵现象比较显著；而预留时间指数和延迟时间指数计算的基准值则是行程时间均值，因此，该指标更多地反映了交通系统运行的稳定性，也即人们对于日常出行经验的可依赖程度。该指标值较高时，说明道路运行的稳定性较差，而它们并不能直接反映道路的运行效率。

3 交通流运行状态分类

3.1 交通拥挤判别方法

由交通流的参数关系可知，交通量与密度的关系为抛物线，当交通量达到最大时，车流密度为最佳密度 Km。当 K ＜Km时，交通流处于不拥挤状态。在该运行状态下，随着车流密度增大，车流量随之增大，直至到达；当 K ＞Km时，交通流运行状态处于拥挤状态。在该运行状态下，随着车流密度的继续增大，交通量反而减小，直至达到阻塞密度，车流暂时停驶[11]。众所周知，行程时间与车流密度成正向关系，即密度越大，所需的行程时间越长。因此，在理论上一条路径单元存在一个最佳行程时间mt，当出行者在该路径单元行驶的行程时间达到mt时，交通量达到最大，mt为交通流不拥挤向拥挤转变的临界行程时间，称之为行程时间阈值。行程时间随交通量变化的示意如图3所示。

图3 行程时间随交通量变化的示意Fig.3 Travel time varying with traffic

取某出发时段内行程时间的均值来表征该时段的行程时间，该时段内匹配成功的数据量均值表征交通量，可以得到行程时间随交通量的变化情况。图4为某快速路路径单元（记为路径单元1），在6:00-10:00内行程时间随交通量的变化情况。

图4 不同出发时段行程时间随交通量的变化Fig.4 Variation of travel time with traffic in different departure time windows

由图4可以看出，当行程时间达到744 s时，交通量达到最大，而后交通量降低，行程时间却继续延长，由此可知，744 s即为该路径单元交通流由不拥挤状态向拥挤状态转化的行程时间阈值。

3.2 交通流运行状态分类

某路径单元在某出发时段发生拥挤的概率计算公式如下：

式中，jN—— 该路径单元在出发时段j内的行程时间样本数据量，取该月该出发时段内的行程时间样本数据总量；

nj—— 该路径单元在该月该出发时段内行程时间大于行程时间阈值 tm的数据量。

图5显示了路径单元1在6:00-22:00内交通拥挤概率的分布情况。

图5 不同出发时段交通拥挤的概率分布Fig.5 Probability distribution of traffic congestion in different departure time windows

由图5可以看出路径单元1拥挤概率在全天的分布分为三种情况：

（1） 0p= ，拥挤概率为0，交通流在该时间段内从未发生交通拥挤；

（2） 1p=，拥挤概率为1，交通流在每天的这个时间段内均发生交通拥挤；

（3）01p＜＜，拥挤概率处在0与1之间，交通流在某些天的该时间段内会发生交通拥挤。

因此，根据交通拥挤的概率分布，可以将全天分为3个时段：

（1） 0p= ，常发性交通流畅通时段。同时，由于交通流是连续变化的，不会出现突变，因此，还可将此时段进行细化，大致可分为自由流时段和自由流至拥挤前的过渡时段。

（2） 1p=，常发性交通拥挤时段。同上也可将该时段细分为初期交通拥挤时段、稳定交通拥挤时段和交通拥挤开始消散时段。

（3）01p＜＜，非常发性交通拥挤时段，也即交通拥挤时有发生的时段。

4 不同交通流运行状态下的行程时间可靠性分析

从2.2相关性分析可知，TTI能更好地从运行效率角度反映行程时间可靠性，而LATI 能更好地从稳定性角度反映行程时间可靠性，因此，分别选取TTI和LATI 作为行程时间可靠性效率性和稳定性两个层面的评价指标，探讨行程时间可靠性与交通流运行状态的关系。

图6为路径单元1TTI、LATI 指标和拥挤概率的分布图。可以看出：对于TTI指标，其变化趋势与交通拥挤的分布趋势几近一致，行程时间可靠性的分布由高到低依次是：常发性交通流畅通时段、非常发性交通拥挤时段、初期拥挤时段和拥挤开始消散时段、稳定交通拥挤时段，行程时间可靠性的分布与交通流的运行效率完全一致。

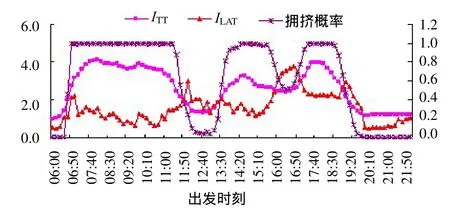
图6 行程时间可靠性与交通流运行状态的关系Fig.6 Relationship between the travel time reliability and operation status of the traffic flow

对于LATI 指标，常发性交通流畅通时段行程时间可靠性最高；其次是稳定交通拥挤时段；在交通流转变时段，如初期交通拥挤时段、拥挤开始消散时段以及非常发性交通拥挤时段，行程时间可靠性最低，分析原因如下：

（1）在常发性交通流畅通时段，车辆行驶速度相对自由，行程时间较为稳定；而在稳定交通拥挤时段，由于交通流处于持续拥挤状态，行程时间的波动空间较小，行程时间较为稳定，但是，由于不同日期同一时段的拥挤程度不同，行程时间仍表现出一定的波动性，其波动程度稍高于常发性交通流畅通时段。

（2）在交通流的转变时段，不同日期交通拥挤开始时间、初期拥挤持续时间、拥挤开始消散时间的提早或延迟，以及某些日期偶发性交通拥堵的发生，使得行程时间表现为较大的波动性，行程时间的可靠性较差。

5 结 论

本文在重新定义行程时间可靠性的基础上，通过统计分析的方法，验证了行程时间可靠性随交通流的变化情况，主要研究结论如下：

（1）行程时间可靠性作为道路可靠性的评价指标，应该能全面反映道路运行状态的可靠性，包括道路运行效率层面的可靠性（即道路实现其运输功能的程度）和道路运行稳定性层面的可靠性（即道路功能发挥的稳定程度）。仅从一个角度分析行程时间可靠性是不科学、不客观的。

（3）从效率层面讲，行程时间可靠性与交通流的拥挤情况（是否拥挤、拥挤程度）变化趋势完全一致；从稳定性层面讲，与行程时间可靠性密切相关的是交通流是否存在转变，在稳定交通拥挤时段，虽然道路的运行效率较低，但是，运行的稳定性却较高。出行者可以根据自己的偏好选择高效率、高延误风险的道路或是低效率、低延误风险的道路。研究结论与人类主观经验基本一致，说明行程时间可靠性分两层内涵定义的科学性。

（4）交通拥挤是致使交通效率低下的本质原因，同时偶发性交通拥挤的发生也是致使行程时间较大波动的主要原因，只有抑制交通拥挤的发生，交通系统的行程时间可靠性才会得到根本保障。

[1] Elefteriadou Lily, Cui Xiao. A framework for defining and estimating travel time reliability [C].Transport Research Board Annual Meeting CD-ROM, Washington D. C., 2007.

[2] 余艳春，邵春福，郭钰愫，熊志华．基于实时数据的路网行程时间可靠度模型研究[J]．现代交通技术，2006，(2)：70-73.

[3] 高爱霞，陈艳艳，任福田．基于蒙特卡罗模拟方法的快速路运行时间可靠度研究[J]．公路交通科技，2006，23(11)：126-132.

[4] 张 勇，王世明，杨晓光．信号控制道路行程时间可靠度计算与实证[J]．同济大学学报(自然科学版)，2009，37(6)：772-776.

[5] 陈 琨，于 雷．基于对数正态和分布的路径行程时间可靠性模型[J]．北京交通大学学报，2009，33(3)：35-39.

[6] Lyman Kate, Bertini Robert L. Using travel time reliability measures to improve regional transportation planning and operations[C]. Transport Research Board Annual Meeting, Washington D. C., 2008:1-10.

[7] Mazloumi Ehsan, Currie Graham, Sarvi Majid.Assessing measures of transit travel time variability and reliability using AVL data [J]. Journal of Transport Geography, 2010, 18:419-425.

[8] Chen Kun, Yu Lei, Guo Jifu. Characteristics analysis of road network reliability in Beijing based-on the data logs from tax[C]. Transport Research Board Annual Meeting CD-ROM, Washington D. C., 2007.

[9] 陈喜群，杨新苗，史其信．城市道路车牌识别系统在交通管理中的应用[A]．第四届智能交通年会论文集[C]，青岛：2008: 271-276.

[10] 叶中行，王蓉华，徐晓岭，白云芬．概率论与数理统计[M]．北京：北京大学出版社，2009.

[11] 任福田，刘小明，荣建等．交通工程学[M]．北京：人民交通出版社，2005．