差动自感式磁流变阻尼器力学性能分析

胡国良，茹毅，王红

(1.华东交通大学机电工程学院，江西南昌330013;2.浙江大学流体动力与机电系统国家重点实验室，浙江杭州310027)

磁流变阻尼器(MRD)作为半主动控制系统的重要组成部分，被广泛应用于建筑及机车车辆减振抗震领域。其动态连续减振机制为:依靠灌注于阻尼器内部的磁流变液随输入电流的变化产生不同剪切屈服应力，使阻尼器产生可控阻尼力[1－2]。随着对MRD研究的深入，其大阻尼力、高可调范围、动态连续可调的优势被进一步挖掘。但在实际半主动控制系统应用中，MRD 往往需要与位移传感器结合才能充分发挥其优势作用，因而需要在结构设计时考虑配套位移传感器的安装与维护，这样不但提高了安装空间和维护成本，也在一定程度上限制了磁流变阻尼器的工业应用[3]。

基于此，美国MTS 公司于1999年运用磁致伸缩原理成功开发出一种具备速度自传感功能的MR 阻尼器[4]。重庆大学的王代华提出一种磁电式相对位移自传感的原理与方法，为磁流变阻尼器集成传感器提供了一种新的思路[5－6]。作者基于差动自感应原理，提出了一种磁流变阻尼器位移自传感方法，同时设计了一种集阻尼力可控及相对位移传感于一体的新型差动自感式磁流变阻尼器(Differential Self-induced Magnetorheological Damper，DSMRD)，并从理论和仿真两方面具体分析了DSMRD 磁场分布、力学特性及阻尼力动态特性。

1 DSMRD 工作原理及阻尼力产生原理

所设计的DSMRD 如图1所示，主要由组合式活塞(由元件3、4、5组成)、不导磁绕线钢筒6、高导磁外套筒8、活塞杆1、浮动活塞7、左端盖2 和右端盖9组成。其中组合活塞头3 将阻尼器内部分割成两个压力区Ⅰ和Ⅱ，内部充满磁流变液。浮动活塞7与右端盖组成腔体Ⅲ，内部填充高压气体。当活塞头3 内的励磁线圈通入直流电流时，在活塞头两端的导磁部分产生磁场，穿透绕线钢筒6 后沿外套筒8 进入活塞头压线板5，最后形成闭合磁路。此时磁路缝隙内的磁流变液被磁化，当活塞运动时产生高强度剪切屈服应力，从而形成一定的阻尼力。通过控制输入电流的大小，可控制输出阻尼力。磁路经由活塞头一端穿过绕线钢筒后由导磁外套筒回到活塞头另一端。由于磁场穿过绕有感应线圈的钢筒时会在线圈内产生感应电动势，通过对感应电动势信号进行分析即可得到活塞的相对位移。

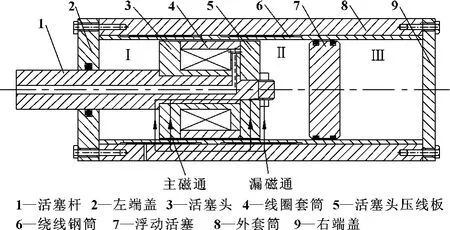
图1 DSMRD结构简图

由于绕线钢筒为不导磁材料，因而会在主磁通两侧出现一定量的漏磁通。处于磁路中的磁流变液受到磁场磁化作用后固化，随着活塞头的轴向运动，在阻尼间隙中经过磁化的磁流变液在活塞头外壁与绕线钢筒内壁之间产生高强度剪切屈服应力，从而使活塞杆达到对外输出阻尼力的目的。

采用Bingham 本构关系理论构建阻尼器力学模型[7－8]，可知剪切阀式磁流变阻尼力Fsv由剪切阻尼力Fs与阀式阻尼力Fv合成，即:

其中:剪切式磁流变阻尼力Fs可表示为:

阀式磁流变阻尼力Fv可表示为:

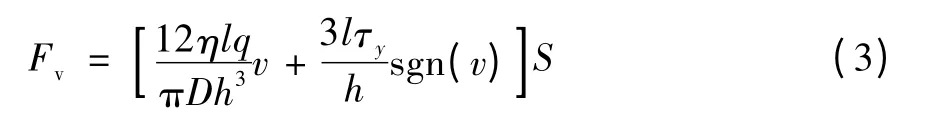
式中:η为磁流变液黏度，l为磁场有效长度，S为有效面积，q为磁流变液体积流量，D为活塞头直径，d为活塞杆直径，h为间隙宽度，v为活塞头运动速度，τy为磁流变液剪切屈服强度。

由于阻尼器右侧设有浮动活塞和右端盖组成的压缩气室Ⅲ，为保证阻尼器活塞能够轴向运动，腔Ⅰ、Ⅱ和气室Ⅲ在活塞拉伸、压缩阶段压力分布情况并不相同。其中压缩阶段Ⅰ、Ⅱ、Ⅲ内压力为pⅠ＜pⅡ=pⅢ，因此磁流变液由Ⅱ腔向Ⅰ腔流入。由于气室Ⅲ左端为可移动悬浮活塞，因此实际流入Ⅰ腔内的磁流变液体积应为活塞头3与浮动活塞7 移动体积之差。由于Ⅰ腔内体积增大值与流入磁流变液体积相等，所以压缩阶段的体积流量q1可以表示为:

拉伸阶段Ⅰ、Ⅱ、Ⅲ内压力为pⅠ＞pⅡ=pⅢ，所以磁流变液由Ⅰ腔向Ⅱ腔流出，流入Ⅱ腔磁流变液体积为Ⅰ腔减少体积，拉伸阶段的体积流量q2可以表示为:

故:q1=q2

Ⅰ腔内有效面积为:

由于DSMRD 拉伸、压缩阶段体积流量q 相同。把式(5)和式(6)代入到式(3)可得:

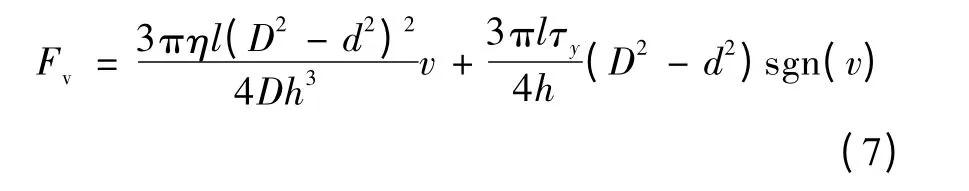
DSMRD 压缩阶段与拉伸阶段气室Ⅲ内压力分布虽然不同，但其产生的流量相同。将所得剪切阻尼力与阀式阻尼力合成后，得到剪切阀式阻尼力:

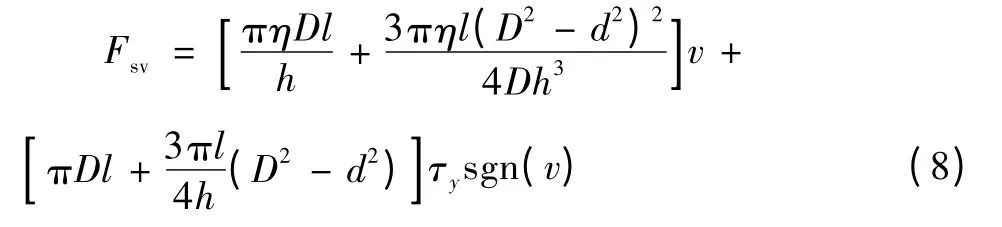
2 DSMRD 磁场有限元建模与仿真

2.1 Maxwell有限元模型

为了准确预估DSMRD 实际工作性能，利用电磁场有限元分析软件Maxwell 建立了DSMRD 二维平面磁场有限元分析模型。首先根据磁流变阻尼器初定的各部分尺寸及材料进行模型构建，考虑到磁流变阻尼器截面为轴对称图形，为了降低计算量，在不影响仿真结果的前提下取截面的1/2 作为研究对象，如图2(a)所示。接着对模型进行网格划分，其中活塞头、活塞头压线板、外套筒部分采用最大长度小于0.04 mm的网格进行划分，如图2(b)所示。

图2 DSMRD仿真模型及有限元模型

2.2 Maxwell 静磁场仿真分析

静磁场仿真分析时，设定静态电流源激励I=2.5 A，模型边缘加载Vector Potential 边界条件后进行仿真，所得磁感线分布、磁感应强度分布和磁场强度分布分别如图3(a)、(b)和(c)所示。从图(a)可以看出:活塞头上下部分对称均匀分布有漏磁通。从图(b)可以看出:工作间隙中分布着强磁场。由于磁流变液的磁化与间隙内的磁场强度密切相关，因此着重从间隙内磁场强度H 进行分析。图(c)中磁场强度最大的区域出现在活塞头上、下两导磁端与钢筒内壁组成的磁流变液间隙区域。选取上导磁端与钢筒内壁的磁流变液间隙区域为分析区域，进行数据提取，得到如图4所示的工作间隙磁场强度分布图。

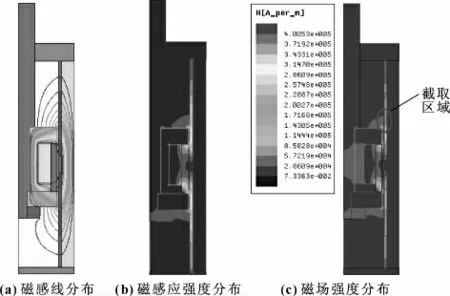
图3 DSMRD 磁场、磁感应强度及磁场强度分布

由图4可知:间隙初始位置时的磁场强度H为140 kA/m，随着位置逐渐向中部靠近，磁场强度逐渐降低，并在靠近几何中部的位置达到50 kA/m的最低值;在远离几何中部之后，磁场强度慢慢增强，并在9～10 mm的位置上迅速提升至300 kA/m以上。参照如图5所示的Lord 公司132DG 磁流变液τ－H曲线[9]可知:磁场强度H与磁流变液剪切屈服应力τy为非线性变换关系，磁场强度在50 kA/m时，τy为10 kPa以上;当磁场强度到达300 kA/m时，磁流变液处于饱和状态，能够产生约为45 kPa的剪切屈服应力。由此可知，DSMRD 完全能够提供将磁流变液完全磁化的磁场强度H。

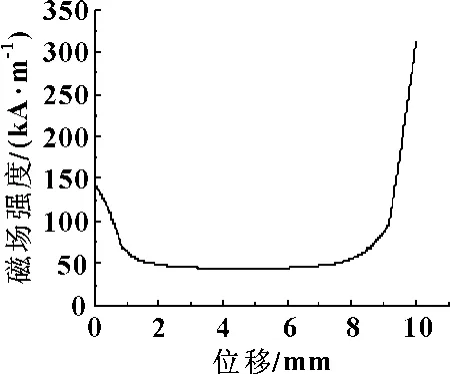
图4 工作间隙磁场强度分布图

图5 磁流变液τ－H曲线

3 MATLAB 建模仿真与数据分析

3.1 MATLAB 建模

利用MATLAB的GUI功能设计了一个如图6所示的DSMRD结构设计试算模块，通过该试算模块能够在设计初期通过更改结构尺寸及材料获得各尺寸结构、材料与阻尼力、功率和缠绕线圈匝数之间的关系。从低能耗、小尺寸、满足阻尼力输出的角度出发，选择符合设计要求的结构尺寸，最大限度降低工作量和设计周期。但是，由于该模块为静态试算模块，不能动态反映阻尼力与电流、速度的关系，需要在结构确定的情况下进行动态仿真。

图6 DSMRD结构设计试算模块

图7为DSMRD 阻尼力仿真试算模块，通过选择不同的磁流变液和不同的结构参数，得到阻尼力。

图7 DSMRD 阻尼力试算模块

图中所示阻尼力为设计预估阻尼力，由于该模块为静态试算模块，因此所得阻尼力值为瞬时值。该模块的设计意义在于:如果设计要求值小于且接近该试算值，则说明尺寸结构大体符合要求，可进行下一步动态仿真;若设计要求值与该试算值相差过大，则需要调整结构参数，重新进行试算。

3.2 Simulink 动态仿真及数据分析

为了获取DSMRD 力学性能的动态数据，建立了用于分析DSMRD 阻尼力的Simulink 动态仿真系统，系统框架如图8所示。

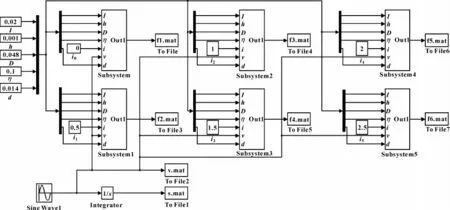
图8 Simulink仿真系统图

该仿真系统由6个子模块组成，每个子模块设定不同的输入电流值，相当于6个DSMRD 在不同电流条件下同时工作。每个模块输入同一结构参数，使阻尼器结构参数保持一致，使建立的数学模型结构相同;再通过对磁流变液进行数学建模，建立磁流变液仿真模块模拟阻尼器中的磁流变液材料，阻尼器结构与磁流变液材料仿真模块共同构成Simulink仿真系统核心。系统外部输入包括结构参数输入和运动激励输入;结构参数输入用来限定阻尼器结构;运动激励输入使阻尼器在运动激励条件下产生与激励信号对应的动态阻尼力。该系统能够模拟DSMRD 阻尼力F 加载不同波形、幅值、频率条件下的变化情况，通过对不同位置S、速度v与阻尼力F的比较得到数据点集，进而得到DSMRD的力学特性。在Simulink系统结构参数中输入预设结构参数。幅值3 cm、频率1 rad/s的正弦波激励作为阻尼振动激励，得到图9所示阻尼力速度曲线和图10所示阻尼力位移曲线。

从图9可知:DSMRD 阻尼力在出现运动趋势时就迅速增大到工作阻尼状态，响应可视为瞬时响应，当到达工作阻尼状态后阻尼力随速度增加呈线性低速增长，直到行程结束。从6个输入不同电流值模块的横向对比可以看出，I=0时，没有阻尼力瞬时增大现象;I=0.5～1.5 A时，阻尼力输出值增大明显;I=2～2.5 A时，增大幅度降低明显。最大阻尼力出现在I=2.5 A、v=3 cm/s时，约为4 800 N;最小阻尼力出现在I=0、v=0时，为0。

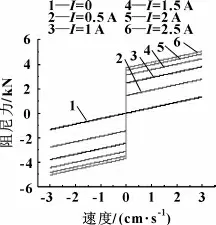
图9 阻尼力与速度关系曲线

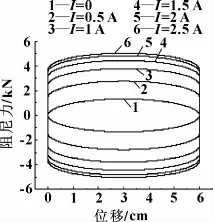
图10 阻尼力与位移关系曲线

由图10可知:DSMRD 活塞起始于上极限位置，受到外部运动激励后，阻尼力瞬时增大到工作阻尼状态，在s ＜3 cm时，阻尼力缓慢增大，s=3 cm时达最大值，最大阻尼力约为4 800 N，s ＞3 cm时阻尼力缓慢降低至初始阻尼力。当s=6 cm时，阻尼力瞬时反向至负向并达到工作阻尼状态。从6个输入不同电流值模块的横向比较可以看出，I=0时，输出阻尼力较低;I=0.5～1.5 A时，阻尼力输出值增大明显;I=2～2.5 A时，增大幅度明显降低。最大阻尼力出现在I=2.5 A、s=3 cm时，约为4 800 N。

4 结论

设计了一种新型差动自感式磁流变阻尼器，基于Bingham 本构模型原理，分析了DSMRD的力学性能。通过Maxwell 电磁场仿真软件对所设计的阻尼器进行了静态磁场仿真分析、MATLAB 静态阻尼力试算、Simulink 动态阻尼力仿真，获得了DSMRD的力学性能。对得到的DSMRD 性能数据进行分析后得出如下结论:

(1)DSMRD 静态磁场仿真结果符合剪切阀式磁流变阻尼器磁路磁场分布特性，通过量化磁场数据确定，DSMRD结构能够产生磁化间隙内磁流变液所需的高强度磁场。

(2)MATLAB 静态试算模块试算幅值小于且接近Simulink仿真最大值，表明试算结果具备可信度，并能在保证设计的情况下，有效降低工作量和缩短研发周期。

(3)Simulink仿真系统能够有效地模拟磁流变阻尼器的运动规律和力学特性。将仿真系统应用于阻尼器的结构设计研发环节，能显著降低实验成本，减少研发周期。

【1】LI W H，WANG X Y，ZHANG X Z，et al.Development and Analysis of a Variable Stiffness Damper Using an MR Bladder[J].Smart Materials and Structures，2009，18(7):1－8.

【2】张克余，刘荣，王松根.基于磁流变阻尼器的半主动控制方法研究[J].机床与液压，2010，38(23):9－12.

【3】GIORGETTI A，BALDANZINI N，BIASIOTTO M，et al.Design and Testing of a MRF Rotational Damper for Vehicle Applications[J].Smart Materials and Structures，2010，19(6):1－8.

【4】余淼.汽车磁流变半主动悬架控制系统研究[D].重庆:重庆大学，2003.

【5】DAVID S N，STEPHEN W S，ARNOLD F S，et al.Magnetostrictive Linear Displacement Transducer for a Shock Absorber:US，5952823[P].1999－09－14.

【6】WANG D H，BAI X X，LIAO W H.An Integrated Relative Displacement Self-sensing Magnetorheological Damper:Prototyping and Testing[J].Smart Materials and Structures，2010，19(10):1－19.

【7】臧彦升，谢光汉，黄超灵.磁流变阻尼器力学模型动态特性实验研究[J].机床与液压，2008，36(4):299－301.

【8】周云，谭平.磁流变阻尼控制理论与技术[M].北京:科学出版社，2007.

【9】http://www.lord.com/products-and-solutions/magneto-rheological-(mr)/product.xml/1645/2.