河南省金属切削机床生产能力的智能预测

李建伟，田辉，刘军

(河南农业大学机电工程学院，河南郑州 450002）

河南省金属切削机床生产能力的智能预测

李建伟，田辉，刘军

(河南农业大学机电工程学院，河南郑州 450002）

金属切削机床生产能力的预测对于了解一个地区机床工业的发展水平和市场供应能力具有重要意义。以2005年至2010年河南省金属切削机床生产能力的统计数据为样本，利用改进的BP神经网络建立了河南省金属切削机床生产能力的预测模型，并对模型的预测能力进行了仿真验证。验证表明该模型的预测相对误差低于0.1%，可以满足预测的需要。对河南省2011年、2012年和2013年的金属切削机床生产能力进行了预测，预测结果表明在未来三年内河南省金属切削机床的生产能力将总体保持稳定，具体表现出“先增加后减少再增加”的波动趋势。

金属切削机床;BP神经网络;生产能力;预测

金属切削机床是机械制造装备的重要分类，在机械制造业中具有重要地位，应用非常广泛［1－2］。金属切削机床制造业是生产金属切削机床的行业，担负着为各种机械制造企业提供先进的制造技术与优质高效的机床设备的任务，该行业的发展状况对整个机械制造业，乃至各个工业部门的发展都有重要的影响。可以说，一个国家或地区的金属切削机床的生产能力和水平在很大程度上反映了这个国家或地区的工业生产能力和科学技术水平。对河南省金属切削机床的生产能力进行预测，可以为了解河南省未来的金属切削机床制造业的供应能力和发展水平提供重要的参考依据，这对于宏观调控中调整产业布局，以及生产企业内部调整产品结构都有十分重要的意义。

要合理预测河南省金属切削机床的生产能力，首先要获得河南省金属切削机床生产能力随时间的变化规律。只有获得了该变化规律后，才能预知在未来某时间河南省金属切削机床的生产能力。而金属切削机床生产能力的变化规律十分复杂，涉及到众多因素的影响，如政策因素、产业布局的宏观调控、经济状况、市场因素等。可以说，金属切削机床生产能力的变化是一个典型的非线性过程。对非线性过程的预测一直是学术界的一个研究热点，在目前的研究中，人工神经网络技术应用较为广泛，因此，将其应用于金属切削机床生产能力变化规律的求解。

1 BP神经网络的基本原理及其改进

在各种神经网络中，误差反向传播 (Back Error Propagation，简称BP）神经网络是应用最普遍最成熟的网络模型之一［3－5］。BP神经网络是一种前馈网络，由1个输入层、若干隐含层和1个输出层组成，每层均可包含若干个神经元。各相邻层神经元之间多为全连接方式，而同层神经元之间则无连接［6］。在结构一定的情况下，神经网络的功能参数表现为网络中存储的各连接的权值和各神经元的阈值。理论上来说，一个仅有三层 (即一个隐含层）的BP神经网络就能够以任意精度逼近任意连续函数及其各阶导数［7］。金属切削机床生产能力的变化规律可以看作是一个非线性的函数，要获得该变化规律，归根结底就是一个函数逼近的过程。显然，BP神经网络完全可以用来解决该问题。

BP神经网络的标准算法主要包括信息前向传播和误差反向传播两部分，现有的研究表明，该标准算法存在多项缺陷，突出表现为收敛速度慢和易陷入局部收敛。为了克服这些缺陷，学者们研究出了多种改进的BP神经网络算法。其中，Levenberg-Marquardt数值优化算法 (简称L-M算法）是一种具有较快收敛速度的、适用于中小型网络的改进型BP神经网络算法［8］，文中作者采用该算法来建立河南省金属切削机床生产能力的预测模型。

和普通BP算法相比，L-M算法不仅利用了目标函数的一阶导数信息，还利用了目标函数的二阶导数信息。L-M算法的迭代公式如式 (1）所示［9－10］。

X(k+1）=X(k）－(JTJ+μI）－1JTe (1）

式中:J为包含网络误差对权值和阈值一阶导数的雅克比矩阵;I为单位矩阵;μ为自适应调整参数;e为误差向量。如果训练过程中，μ取很小值，式 (1）就近似于高斯牛顿法，而当μ取很大值时，式 (1）就成为带有较小步长的最速梯度下降法。在L-M算法中，迭代的收敛方向会根据迭代的结果动态调整，以使每次迭代的目标函数值都有所下降。当试探性迭代使得目标函数增加时，μ增大;否则，μ会减小。因此，μ被称为自适应调整参数，也正由于μ的自适应调整，才使得L-M算法的收敛速度得到了大大提高。

2 河南省金属切削机床生产能力的预测模型

2.1 预测模型基本参数的确定

采用改进的BP神经网络模型建立河南省金属切削机床生产能力预测模型的过程，就是确定BP神经网络的结构参数，并对所建立的网络模型进行有效训练的过程。在BP神经网络结构参数的确定中，应充分考虑研究对象的特征和样本数据量的大小。

河南省金属切削机床生产能力的预测，可以看作是对一时间序列数据的预测。在时间序列数据的预测中，常用的一种方法是利用最近n个时间点的数据预测第n+1个数据，此处将该方法称为分步预测法。在分步预测法中，所谓的预测模型就是最近n个时间点的数据和第n+1个数据之间的具有普遍适用性的函数关系。

为获得河南省历年的金属切削机床生产能力的统计数据，笔者查阅了大量的年鉴文献，仅在文献［11］中获得了2005—2010年该指标的统计数据，如表1所示。由于样本数据只有6个，分步预测法中的n取值不宜较大，此处确定为3，即用连续三年的金属切削机床生产能力的数据去预测第四年的数据。

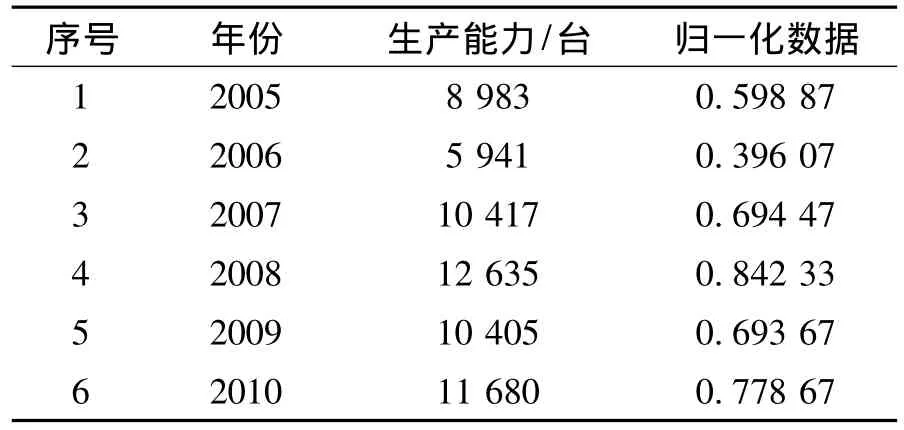
表1 2005—2010的原始样本数据及归一化数据

由于每次训练需要输入3个独立数据，确定神经网络的输入层神经元数目为3。采用分步预测时，每次的输出量只有一个，因此，确定神经网络的输出层神经元数目为1。考虑到样本数据有限，神经网络的结构不宜太复杂，确定神经网络的隐含层数目为1，隐含层神经元数目根据Kolmogorov定理确定为7。为了较好地逼近非线性关系，隐含层和输出层神经元的激励函数分别采用正切型和对数型Sigmoid函数。最终确定的神经网络预测模型的结构示意图如图1所示。

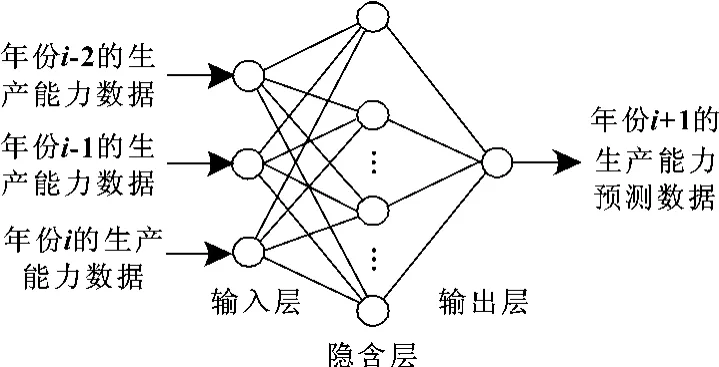
图1 预测模型的结构示意图

2.2 训练样本的处理

从表1中可以看出，各年份的金属切削机床生产能力的数值较大，为了降低神经网络模型的训练难度，需要对这些样本数据进行归一化处理。根据实际情况，归一化时，将所有数据均除以15 000台 (保留5位小数），这样原始样本数据就转化为如表1所示的0～1之间的归一化数据。利用归一化数据来训练网络和进行预测。

按照分步预测法的思想，得到训练预测模型时的输入、输出矩阵分别如式 (2）和式 (3）所示。

3 预测模型的训练与验证

3.1 预测模型的训练

为使训练出的预测模型充分逼近河南省金属切削机床生产能力的变化规律，将网络训练时的期望精度定为0.000 1，采用L-M算法对建立的神

经网络模型进行训练。从图2中可以看到，仅经过4步训练，网络即达到了期望精度的要求，这也验证了L-M算法的快速收敛特性。

图2 预测模型训练时的误差收敛曲线

3.2 模型预测能力的验证

为检验所建立BP神经网络预测模型的预测能力，需要进行验证实验。将式 (2）所示的输入矩阵输入到神经网络模型中，比较所获得的仿真预测数值和真实数值的差异即可检验该模型的预测能力。实验结果如图3和表2中2008—2010年部分所示，从图3中可以直观看出预测值和真实值吻合良好，从表2中可以看出预测的绝对误差和相对误差均很小，其中相对误差均在0.1%以下。这些表明:所建立的预测模型预测能力强，预测精度高，可以满足预测的需要。

4 预测

采用分步预测法，以2008—2010年的河南省金属切削机床生产能力的归一化数据组成输入向量，通过预测模型可获得2011年的预测数据;再以2009年、2010年的归一化数据和预测的2011年数据组成输入向量，可以获得2012年的预测数据;同理可获得2013年的预测数据。所获得的预测数据如表2中所示。以上获得的数据还是归一化后的数据，要获得最终的河南省金属切削机床生产能力的预测数据，还需要进行反归一化。反归一化时，将表2中的预测数据均乘以归一化参数15 000台，得到预测数据如下:2011年，11 972台;2012年，10 775台;2013年，119 99台。可以看出:未来三年内河南省金属切削机床的生产能力将围绕11000台附近窄幅波动，总体上保持稳定;从具体数值上看，将表现出“先增加后减少再增加”的波动趋势。

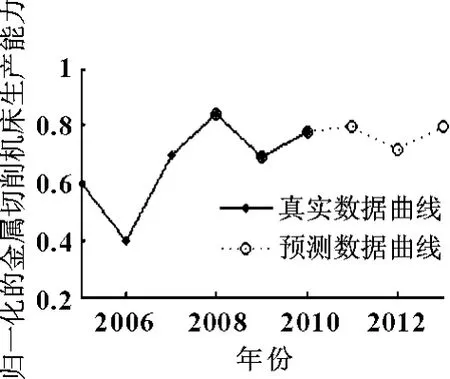
图3 归一化后的真实值与预测值的对比曲线

表2 归一化后的真实值与预测值的对比表

5 结束语

对金属切削机床的生产能力预测进行了尝试。采用改进后的BP神经网络建立了河南省金属切削机床生产能力的预测模型，并预测出了未来三年河南省金属切削机床生产能力的数据和变化趋势。所获得的研究结论，对于了解河南省未来的金属切削机床制造业的发展趋势具有一定的参考价值。

但要指出的是，文中所采用的样本数据仅有6个，属于典型的短序列的预测。短序列的预测，本身就很难保证预测的有效性。另外，金属切削机床的生产能力还可能会受到各种干扰因素的影响。因此，所得到的预测数据仅供参考。

【1】冯辛安．机械制造装备设计［M］．北京:机械工业出版社，2006．

【2】戴曙．金属切削机床［M］．北京:机械工业出版社，1993．

【3】郑立华，李民赞，潘娈，等．基于近红外光谱技术的土壤参数BP神经网络预测［J］．光谱学与光谱分析，2008，28(5）:1160－1163．

【4】卞凤兰，黄晓明，刘睿．城镇化进程中公路网用地的BP神经网络预测模型［J］．东南大学学报:自然科学版，2010，40(5）:1073 －1076．

【5】王凯．铣削加工表面粗糙度的智能预测［J］．机床与液压，2009，37(10）:58 －59，119．

【6】陈祥光，裴旭东．人工神经网络技术及应用［M］．北京:中国电力出版社，2003．

【7】陈明．神经网络模型［M］．大连:大连理工大学出版社，1995．

【8】LERA G，PINZOLAS M．Neighborhood Based Levenberg-Marquardt Algorithm for Neural Network Training ［J］．IEEE Transactions on Neural Networks，2002，13(5）:1200－1203．

【9】HAGAN M T，MENHAJM．Training Feedforward Networks with the Marguardt Algorithm ［J］．IEEE Transactions on Neural Networks，1994，5(6）:989 －993．

【10】黄建军，刘会霞，杨润党，等．基于改进BP神经网络的数控机床振动趋势预测［J］．制造技术与机床，2009(4）:63－65．

【11】河南省统计局，国家统计局河南调查总队．河南统计年鉴2011［M］．北京:中国统计出版社，2011．

Intelligent Prediction on Production Capacity of Metal-cutting Machine Tools in Henan Province

LIJianwei，TIAN Hui，LIU Jun
(Mechanical＆ Electrical Engineering College，Henan Agricultural University，Zhengzhou Henan 450002，China）

The prediction on production capacity ofmetal-cutting machine tools is important for understanding the development level ofmachine tool industry and the supply capacity ofmarket in a region．Historical statistical data of Henan province's production capacity ofmetal-cuttingmachine tools from 2005 to 2010 were used as samples．Improved BP neuralnetwork was used to establish the production capacity predictionmodelofmetal-cuttingmachine tools in Henan province．A simulated experimentwas carried out to verify themodel's predictive ability．The maximal relative error in all predicted points lowers than 0.1%;it shows that the prediction model is available．Production capacity data ofmetal-cuttingmachine tools in 2011，2012，and 2013 were predicted．Predicted result shows that the production capacity ofmetal-cuttingmachine tools in Henan province in the next three years will generally remain stable，and will show a trend as“increase-decrease-increase”in detail．

Metal-cuttingmachine tool;BP neural network;Production capacity;Prediction

TG508;TP183

A

1001－3881(2013）9－071－3

10．3969/j.issn.1001 －3881.2013.09.020

2011－11－27

李建伟 (1978—），男，工学硕士，讲师，主要从事机械电子工程及人工智能应用等方面的研究。E－mail:hauljw@163.com。