运动分离偏心型食品搅拌机轨迹优化及运动仿真
2013-03-20吴玉国许正华时礼平
吴 胜 吴玉国 许正华 时礼平 陈 彬
(1.安徽工业大学,安徽 马鞍山 243032;2.安徽华菱西厨装备股份有限公司,安徽 马鞍山 243131)
多功能食品搅拌机是馒头、方便面等面食类食品加工中的主要机器,广泛用于面点房、宾馆、餐馆及家庭制作蛋糕、面点等各种食品的加工[1]。传统立式中心搅拌的搅拌轴设置在桶的中心线上,工作时会在搅拌器中心附近产生明显的涡流回转区域,使搅拌不均匀、效果变差。并且现有的食品搅拌机需要使用两个电机分别提供搅拌机中搅拌器的旋转搅拌及搅拌桶的上下提升运动的动力,这样造成食品搅拌机的制造和使用成本增加,不利于搅拌机的批量生产[2-4]。
本试验设计一种运动分离偏心型食品搅拌机,并推导出搅拌器的运动轨迹的理论方程。结合Matlab和Solidoworks软件对运动分离型偏心食品搅拌机进行了轨迹优化和运动仿真。
1 运动分离型偏心食品搅拌机工作原理
搅拌器是搅拌机的主要工作部件。根据搅拌器的安装形式不同,会产生不同的流场,使搅拌的效果有明显的差别[5,6]。在运动分离型偏心式搅拌机中,搅拌器采用偏心式安装,搅拌器既会围绕其本身的轴线自转,同时又会绕搅拌桶的中心轴线公转,实现搅拌器的行星运动。使用偏心式搅拌装置能有效防止面粉在搅拌器中心附近产生涡流回转区域,使液流在各处的压力分布不同,从而加强了液层间的湍动,使搅拌效果得到明显的改善。
运动分离型偏心食品搅拌机通过单向轴承使电机的正转和反转分别实现搅拌器的搅拌运动和搅拌桶升降运动,当电机正转时,电机动力传至搅拌器,对物料进行搅拌,而搅拌桶升降装置不运动,当电机反转时,电机为搅拌桶升降装置提供动力,使搅拌桶上升或下降,且搅拌器不运动。用一个电机即可提供搅拌机中搅拌器的旋转搅拌运动及搅拌桶的升降运动的动力。
运动分离型偏心食品搅拌机结构如图1所示,电机的输出轴通过增长轴套与联轴器相连,小锥齿轮与轴套之间装有单向轴承,联轴器与横向轴之间也装有单向轴承。电机正转时,单向轴承锁紧,单向轴承松开,电机动力通过大锥齿轮、中心轴将动力传至行星架,行星轴上端安装有行星齿轮,行星齿轮与内齿圈啮合,行星架转动,螺旋式搅拌器[7]随行星齿轮一同在公转的同时有自转运动。电机反转时,联轴器与横向轴之间单向轴承锁紧,电机的输出轴与小锥齿轮之间单向轴承松开,电机动力通过横向轴传至蜗杆,蜗杆旋转使蜗轮随之旋转,曲柄随蜗轮一起旋转,从而使搅拌桶上升或下降。
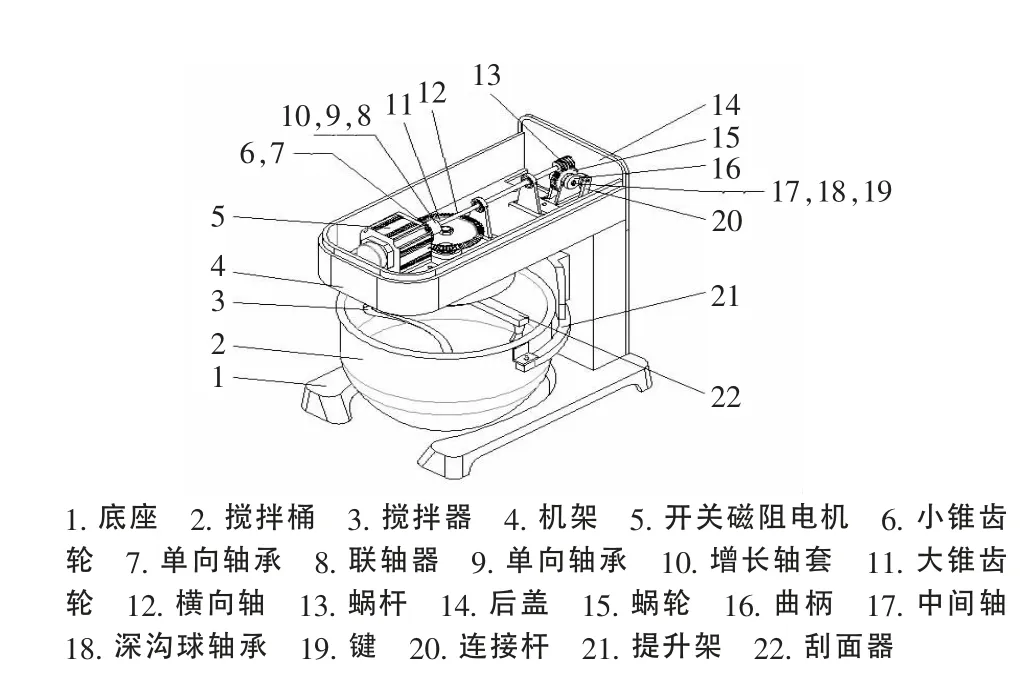
图1 搅拌机装配图Figure1 Assembly drawing of blender
2 运动分离型偏心食品搅拌机搅拌轨迹仿真及优化
运动分离型偏心食品搅拌机,搅拌机叶片既绕本身的轴线自转,其转轴又绕搅拌桶的中心轴公转,以此构成搅拌叶片的行星运动。建立搅拌器运动分析坐标系见图2。
设搅拌器的公转角速度为ω1,自转角速度为ω2,公转角速度为ω1与自转角速度为ω2之比为S,因为搅拌器的行星运动是通过行星齿轮与内齿圈的啮合而实现的,所以搅拌器的自转角速度ω2与公转角速度ω1在数值上与行星齿轮齿数z2和内齿圈齿数z1相关,即,设搅拌器公转的半径为R,自转半径为r,搅拌器的公转半径为R 与自转半径为r 之比为K,即选取搅拌器上一点的运动方程:

图2 搅拌器运动分析Figure2 Motion analysis coordinates of agitator

式中:
ω2—— 搅拌器的自转角速度,rad/s;
r—— 搅拌器的自转半径,mm。
搅拌中心旋转的方程:
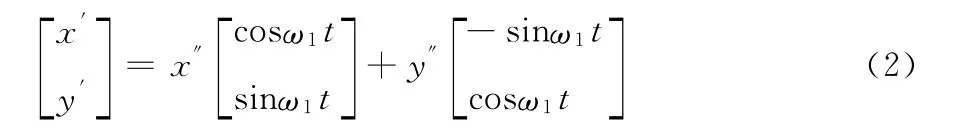
式中:
ω1—— 搅拌器的公转角速度,rad/s。
搅拌中心平移方程:
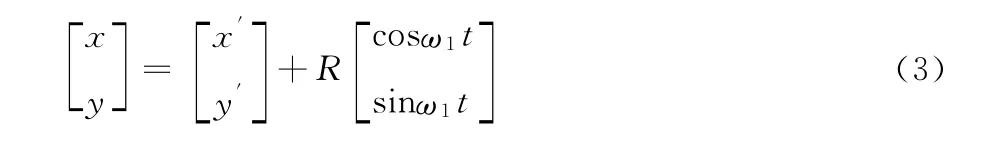
式中:
R—— 搅拌器的公转半径,mm。
将式(1)、(2)代入式(3),可得:
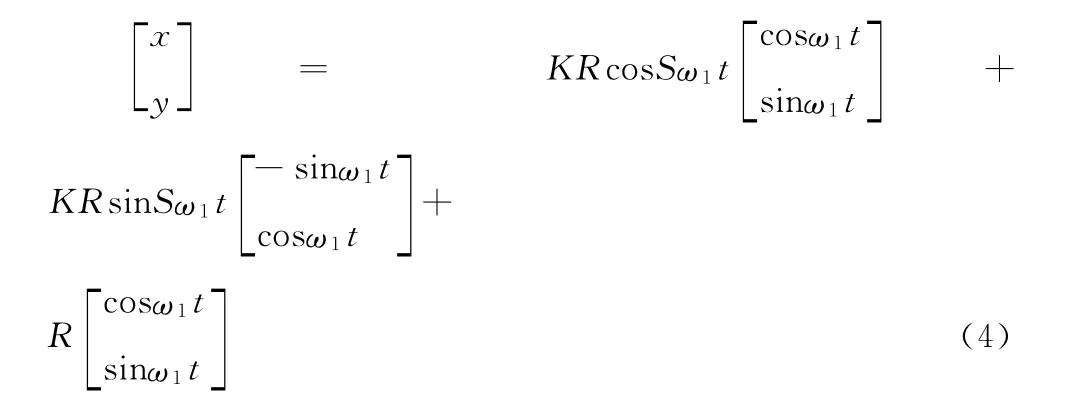
式中:
K—— 公转角速度为ω1与自转角速度为ω2比值,即
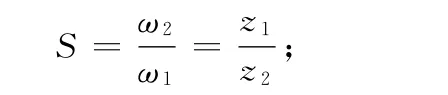
S—— 搅拌器的公转半径为R 与自转半径为r 比值,即
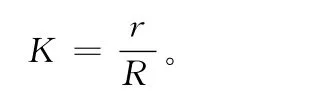
将式(4)进行简化可得:

根据方程(5),使用Matlab软件可绘制得到一系列搅拌器轨迹的图谱。由图3和图4可知,搅拌机叶片运动轨迹的形状和密度与搅拌器的自转和公转速度比S、搅拌器半径和搅拌器公转半径之比K 有关。对比图3(a)、(b)和(c)中搅拌器的运行轨迹图,K 分别取0.75,1,1.25时,当K 取值小于1时,中间会存在搅拌器不能到达的区域,形成搅拌死角,当K 取1.25,轨迹密度和轨迹交叉程度均有所增加,则会较好的克服搅拌死角的存在。将图4与图3中(c)、(d)和(e)进行比较,当S 为自然数时,搅拌器的轨迹是重合的,而当S 取为一个无限不循环小数时,轨迹永不重合,这对于面粉的搅拌是有利的,在实际设计中将S 取为一个有限不循环小数,这样能使搅拌器运行轨迹的重复周期增长,轨迹密度和轨迹交叉程度比S 为自然数时具有显著的优越性。
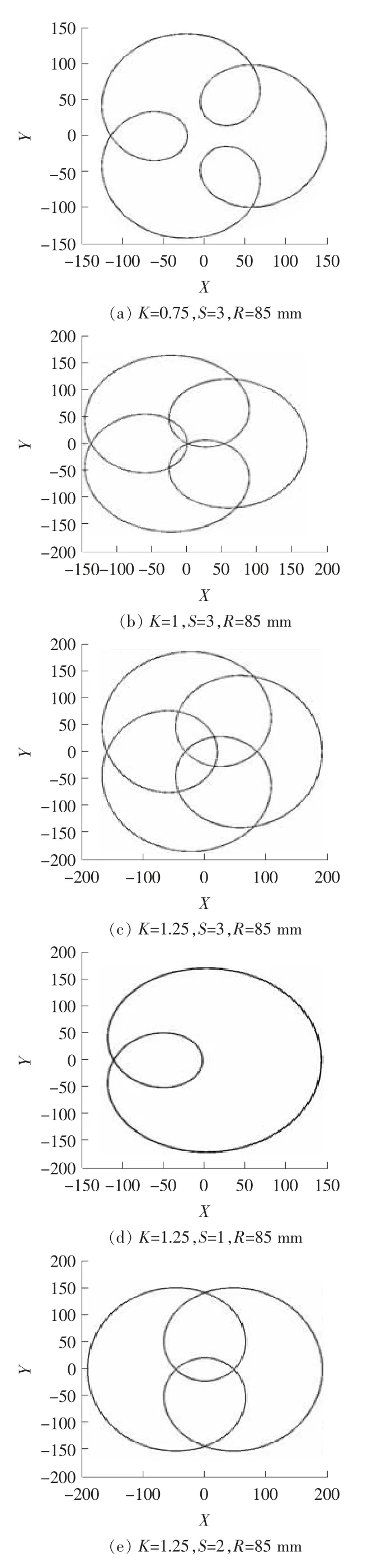
图3 搅拌器轨迹Figure3 Trajectory of agitator

图4 分离型偏心食品搅拌机运动轨迹图(K =1.25,S =π,R =85mm)Figure4 Trajectory of motion separation spiral type food blender(K =1.25,S =π,R =85mm)
3 运动分离型偏心食品搅拌机的运动仿真
3.1 运动仿真参数设置
将已建好的搅拌机三维装配模型导入,在装配模块下直接进入仿真界面,激活Solidworks中的Motion插件。根据搅拌机的运行情况,将搅拌机的机架进行固定,定义为静止部件,其他的零部件则定义为运动部件[8]。通过建立各零部件间的约束可以定义搅拌机中各零部件间是如何连接和相对运动的,在Solidworks Motion中,约束是相对理想化的,设定零部件都是刚性的、且没有质量,没有任何间隙及倾斜,Solidworks中零部件间的装配关系都会转化为Solidworks Motion中的约束,这就会大大节约运动分析的时间[9,10]。分析搅拌机各部分的运动特点和运动要求,中心轴与行星架、行星架与行星轴为转动副,行星齿轮与内齿圈为高副,行星轴与搅拌器采用销连接。Solidworks Motion仿真参数包括基本运动参数和解算器参数。Motion分析每秒帧数设置为25,分辨率及精确接触的精确度采用Solidworks Motion的默认设置。解算器选为WSTIFF 积分器,设定WSTIFF 积分器在为给定的时间内步长搜索求解时所能迭代的最大次数为25,指定最大雅可比验算,其他选项采用默认设置即可。将马达加载在中心轴上,方向设置为顺时针方向,转速设置为15r/min。
3.2 运动仿真结果及分析
得到搅拌器在一个仿真循环内的速度和加速度曲线图,包括X 方向分量、Y 方向分量和幅值,如图5、6所示。拖动仿真工具条上的时间滑块,便可以得到搅拌器在一个搅拌循环内各个时间点的速度、加速度数值,同时在模型上会显示方向。
由图5、6可知,分析速度和加速度的变化规律,分析发现,X 方向分量和Y 方向分量则是在一个仿真循环内为非周期性变化的波动线,但是速度和加速度的幅值图都是余弦曲线。从速度幅值图中可以看出,在一个仿真循环内,搅拌机运动平稳性比较好,搅拌器在0.10,1.43,2.74s3个时刻,搅拌转至搅拌桶的中间位置,离搅拌中心最近,速度达到最小,加速度最大,但速度最小值并不等于0,这是因为K 的取值为1.25,即搅拌器运动轨迹大于搅拌桶半径。搅拌器在0.74,2.10,3.43s3个时刻,搅拌器转至搅拌桶的外缘位置,回转半径最大,速度值达到最大,加速度最小。
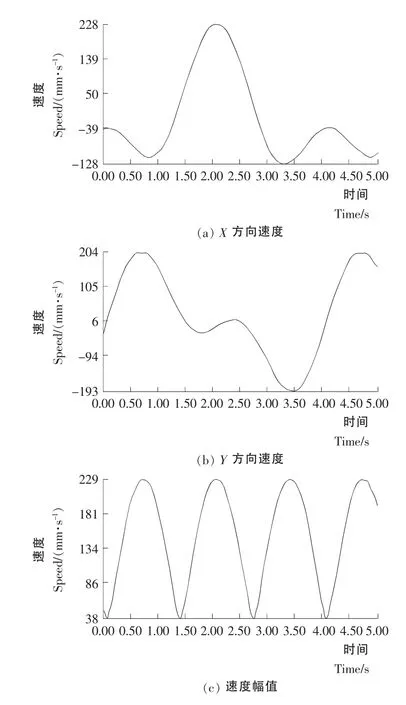
图5 搅拌器速度图Figure5 Speed chart ofagitator
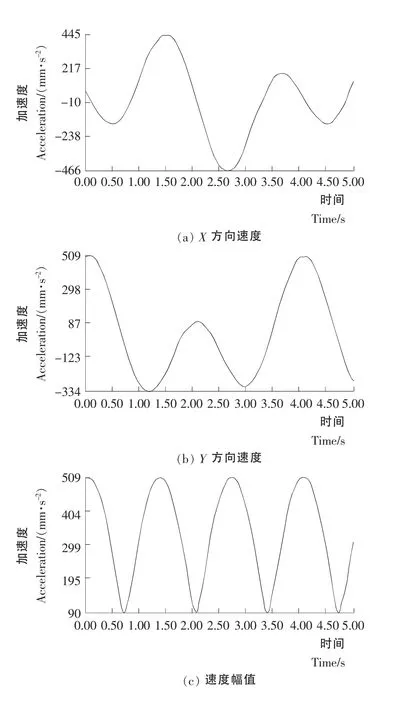
图6 搅拌器加速度图Figure6 Acceleration chart ofagitator
4 结论
(1)当S 值取为π、K 取为1.25时,轨迹密度和轨迹交叉程度均有所增加,搅拌路径比较理想,消除搅拌死角。
(2)在一个仿真循环内,搅拌器完成3个周期的运动,搅拌机运动平稳性比较好;搅拌器转至搅拌桶的中间位置,离搅拌中心最近,速度达到最小,但速度最小值并不等于0,这是因为K 的取值为1.25,即搅拌器运动半径大于搅拌器半径。搅拌器转至搅拌桶的外缘位置,回转半径最大,速度值达到最大,加速度达到最小。
1 陈登丰.搅拌器和搅拌容器的发展[J].压力容器,2008,25(2):33~46.
2 刘海燕,庞明军,魏进家,等.非牛顿流体研究进展及发展趋势[J].应用化工,2010,39(5):194~200.
3 焦海亮,包雨云,黄雄斌,等.高黏度流体混合研究进展[J].化工进展,2007,26(11):1 574~1 582.
4 李力.高黏度流体的复合式搅拌[D].北京:北京化工大学,2012.
5 杨锋苓,周慎杰,张翠勋,等.偏心搅拌槽内固-液悬浮特性研究[J].华中科技大学学报(自然科学版),2012(11):1 064~1 069.
6 杨敏官,冯浪,康灿,等.偏心搅拌槽内颗粒悬浮特性的试验研究[J].水电能源科学,2012,30(4):129~178.
7 吴玉国,吴胜,迟开红,等.搅拌器的结构设计及有限元模拟[J].食品与机械,2013,29(2):130~132.
8 郗向儒,韩锐,阮静.基于Solidworks的运动仿真研究[J].机械设计,2004,21(5):50~52.
9 郑向华.基于Solidworks的机械手运动仿真设计[J].科技视界,2007(24):17~18.
10 周婷.基于ADAMS 的搅拌机运动分析[J].现代机械,2009(1):68~79.
