考虑加速蠕变的岩石蠕变过程损伤模拟方法*
2013-03-19曹文贵袁靖周王江营翟友成
曹文贵,袁靖周,王江营,翟友成
(湖南大学土木工程学院,湖南长沙 410082)
岩石蠕变全过程模拟即蠕变模型是岩石蠕变力学研究的基础内容之一,国内外学者[1-10]对此进行了广泛而深入研究,取得了长足进步.由于岩石蠕变所受影响因素广泛而复杂,现有岩石蠕变模型虽然对岩石稳定蠕变及其之前变形阶段的模拟取得了良好的效果,但是,它们在模拟加速蠕变时仍存在一定不足或缺陷,如何建立出能模拟岩石蠕变全过程尤其是加速蠕变过程的岩石蠕变模型正是本文研究的出发点.
目前,岩石蠕变模型研究的最常用方法主要有2种[3-5].其一,利用实测蠕变曲线采用拟合的方法[3-4],该方法所建立的模型与工程实际吻合程度较高,但是,对于不同的岩石或工程背景,模型拟合的形式、拟合参数的数量都存在不确定性,因而,所建立模型不具有普遍适用性.其二,通过将3种理想材料的元件模型(即虎克体,圣维南体和牛顿体)进行串并联组合建立岩石蠕变模型,利用该方法建立的岩石蠕变模型极其繁多,较有代表性的模型有Maxwell模型、Kelvin模型、Kelvin-Voigt模型、Burgers模型、Bingham模型及西原模型等[5].这类模型能较好地模拟岩石初期至稳定蠕变阶段的变形过程,但无法反映岩石加速蠕变的变形特征,这就使此类模型亦存在很大局限性.
为了模拟岩石加速蠕变过程,国内外学者[6,9]对岩石非线性流变理论进行了广泛而深入的研究,取得了卓有成效的研究成果,主要存在两种基本方法:其一,考虑到现有3种基本元件的局限性,构建出新的理想材料元件[6-7],如非线性粘滞元件、非线性塑性元件等,并将其与传统流变元件进行组合建立出岩石蠕变模型;其二,引进损伤理论,考虑岩石蠕变参数因岩石变形损伤而变化,以损伤因子对岩石蠕变参数进行修正,并基于传统流变元件进行组合建立出岩石蠕变模型[8-9].采用上述两种方法建立出的岩石蠕变模型的确在一定程度上均可以模拟岩石蠕变过程,尤其是模拟加速蠕变过程,但是,这些模型仍存在一定的缺陷与不足,主要表现在如下几个方面.
首先,岩石加速蠕变过程模拟问题属于非线性蠕变问题,即可认为岩石蠕变模型参数呈非定常变化,它们不仅受蠕变量大小的影响,而且,它们随时间的变化率也受应力水平的影响,现有相关蠕变模型更多反映的是蠕变参数受蠕变量大小的影响,无法反映参数变化率与应力大小的关系;其次,现有岩石蠕变模型几乎全部基于基本流变元件或改进流变元件的组合而形成,采用的元件多,致使所建立的模型要么解析式复杂,要么不能得到显式的解析式或根本无法求解,因而,其工程应用受到约束;其三,现有相关模型大多参数繁多,参数的确定存在困难,有的纯粹依靠经验来确定,也有的采用拟合的确定方法,还有的甚至需要采用复杂的优化理论来确定,这就使得模型的应用受到限制.由此可以看出,现有岩石蠕变全过程尤其是加速蠕变阶段模拟方法即蠕变模型存在一定的局限性与不足,有待进一步完善,但无论如何它为岩石加速蠕变过程模拟研究开辟了新的途径.
理想的岩石蠕变模型要求既能模拟岩石蠕变全过程,尤其是模拟岩石加速蠕变过程,同时又要求模型参数少,物理意义明确,而且参数易于确定,这正是本文研究的核心内容,本文将在深入研究岩石蠕变变形机理和变形过程特征的基础上,引入损伤理论,建立出新型的反映岩石蠕变过程的蠕变模型,并提出简单可行的模型参数确定方法,以期完善岩石蠕变模型研究的理论与方法.
1 岩石蠕变机理与蠕变过程特征
岩石蠕变机理与蠕变过程的特征是岩石蠕变模型研究的基础,国内外大量试验研究[5]表明岩石蠕变过程具有明显的阶段性,如图1所示,一般具有如下不同变形段和变形特征:
1)瞬时变形阶段(OA段).由于岩石受到一定应力的作用,必定产生瞬时变形.单轴应力情况下一般可由下式确定:

式中σ0为岩石的蠕变应力;ε0为相应瞬时应变;E0为岩石弹性模量.
2)初始蠕变阶段(AB段),又称为减速蠕变阶段,该段蠕变曲线呈下凹型,应变率随时间增长逐渐减小,直至达到B点时蠕变率达到最小值.
3)等速蠕变阶段(BC段),又称稳定蠕变阶段,该段蠕变曲线近似呈直线形式,应变率保持常数,直至达到C点.

图1 典型岩石蠕变曲线Fig.1 Typical curve of rock creep
4)加速蠕变阶段(CD段).在该变形阶段,蠕变曲线呈上凹型,蠕变率急剧增大,直至岩石破坏,此时,蠕变率达到无穷大.
上述4个变形阶段是岩石典型的蠕变全过程,但研究表明并非任何岩石在任何条件下一定都具有这4个典型变形阶段,而且,每个变形阶段在不同荷载条件下的长短也有所不同,现有研究[6-10]已获得如下认识:
1)岩石在加速蠕变阶段之前,可以称为线性流变过程,其变形主要是黏弹性变形,卸载后基本上可全部恢复,永久变形较小或可忽略;而加速蠕变阶段可以称为非线性流变过程,在开始发生加速蠕变后,黏弹性变形已经稳定,而永久变形越来越大,占总变形的大部分,因此,为了模拟该变形过程,必须引进一个能反映永久变形随时间增大的非线性流变元件,可将岩石蠕变视为线性蠕变与非线性蠕变的迭加.
2)岩石加速蠕变阶段只有在岩石所受应力水平超过屈服应力时才会产生.
3)岩石等速蠕变阶段或稳定蠕变阶段其实是一个蠕变率增长较缓慢的加速蠕变过程,其蠕变曲线表现为近似的直线特征,一般并不会出现这种严格意义的等速蠕变.
4)岩石经历初始蠕变至加速蠕变阶段,岩石最终会破坏,所经历时间称之为岩石蠕变寿命tF,如图1所示,此时,蠕变率达到无穷大,合理的蠕变模型必须反映这一特征.
上述即为目前人们对岩石蠕变机理与蠕变全过程特征的认识,这为本文岩石蠕变模型的建立奠定了良好的基础,下面将在此研究基础上探讨反映岩石蠕变全过程尤其是加速蠕变过程的模拟方法.
2 岩石蠕变全过程模拟方法
由前面岩石蠕变机理与岩石蠕变过程特征分析可知,典型的岩石蠕变全过程可简化为减速蠕变阶段和加速蠕变阶段,现有研究表明[5]采用传统理想材料流变元件的简单组合可以较好地描述减速阶段的变形过程,而对于加速蠕变阶段,目前已有模型和方法的模拟效果并不理想,作者经深入考虑,本文将采用考虑损伤率变化影响的弹塑性损伤元件模型来模拟加速蠕变变形过程,因此,本文拟采用弹塑性损伤元件与黏弹性模型的串联组合来建立岩石蠕变全过程模拟的蠕变模型,其基本的组合形式如图2所示,由此可以看出,岩石总应变ε由弹塑性损伤体应变εep和Kelvin体应变εve组成,可表示为:

式中Kelvin体所表示的黏弹性应变εve可由下式确定[5]:

式中σ0为岩石应力;E1为黏弹性模量;η为黏滞系数;t为蠕变时间.由此可以看出,当t=0时,则εve=0,而当t→∞时,εve→σ0/E1(常数),显然,Kelvin元件模型既不能反映岩石的瞬时变形特性,也不能反映岩石加速蠕变特性,但是,它符合岩石衰减蠕变的典型特征,根据本文建立的岩石蠕变模型(如图2所示),要求本文构建的弹塑性元件模型必须同时反映岩石蠕变的瞬时变形和加速蠕变特性,因此,如何构建反映上述要求的弹塑性损伤体元件模型及其应变分析方法是本文岩石蠕变模型的关键.为此,下面将详细介绍弹塑性损伤元件变形分析的过程与方法.
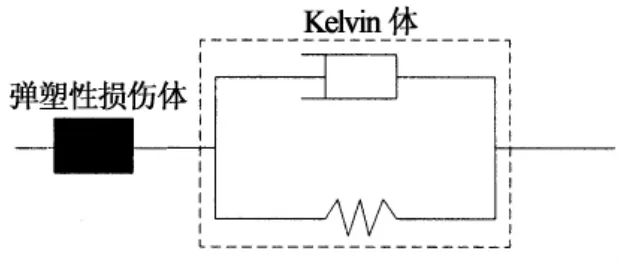
图2 岩石蠕变模型Fig.2 Model of rock creep
取弹塑性损伤体微元,如图3所示,其由损伤和未损伤两部分材料组成,设损伤和未损伤部分材料的截面面积分别为A1和A2,弹塑性损伤体微元截面面积为A,且有:

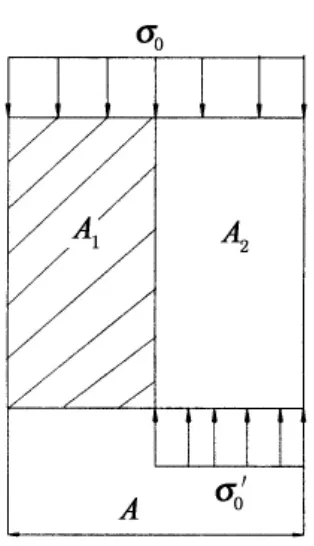
图3 弹塑性损伤体微元受力分析Fig.3 Force analyses of the elastic-plasticity damage cell
并设弹塑性损伤体所受名义应力(即平均应力)为σ0,损伤部分材料不能承受荷载,其荷载全部由未损伤部分承担,其所受应力为σ0′,因此,根据微元的力平衡与几何关系可得:

考虑到式(4)及(5)并定义损伤变量或损伤因子D=1-A2/A,可得:

由于σ0′为未损伤部分材料所受应力,如果假设其应力应变关系服从线弹性虎克定律,并设微元体总应变为εep,未损伤部分材料应变为εep′,则:

式中E0为弹塑性体变形模量.由于损伤和未损伤部分材料紧密混杂在一起,则这两部分材料的变形必须协调,于是,根据变形协调原理可得:

于是,由式(7)及(8)可得:

将式(9)代入式(6)可得:

上式即为本文建立的弹塑性损伤体本构模型即基于Lematrie应变等价性假说[11]的岩石损伤模型.由此可以看出,要建立出岩石弹塑性损伤体本构模型,其关键在于损伤变量D即损伤演化模型的确定.
岩石蠕变损伤与一般损伤的概念有所不同,岩石蠕变的损伤主要是由岩石加载变形时间引起的,对此,Kachanov[12]进行了深入研究,取得了较成熟的研究成果,本文利用其成果可得岩石蠕变损伤率为:

式中C与V为岩石材料参数.据此,Kachanov得到了蠕变损伤变量与时间及蠕变寿命的关系式:

式中tF为蠕变寿命,即岩石蠕变破坏时间.
现有试验和研究表明[5-6],岩石蠕变损伤不是在任何荷载情况下都会发生,只有当应力大于岩石屈服极限σs时,岩石蠕变才会发生损伤,因此,本文最终建立的岩石蠕变损伤演化模型为:

式中α=1/(V+1).
于是,将式(13)代入式(10)即可得到弹塑性损伤体的本构模型为:

再将式(14)及式(3)代入式(2)可得到本文建立的岩石蠕变模型:

引入开关函数〈σ0〉,并令:

则式(16)可写成统一形式:

由此可以看出,本文建立的岩石蠕变模型存在如下特征:
1)如果岩石出现加速蠕变阶段,即σ0>σs及〈σ0〉=1,则当t→tF,ε→∞且dε/dt→∞,显然,该模型可以反映岩石加速蠕变阶段的特征.
2)当t=0时,则ε=σ0/E0,因此,该模型可反映岩石蠕变的瞬时变形特征.
3)如果岩石不出现加速蠕变阶段即σ0<σs及〈σ0〉=0,则式(17)可改写为:

显然,其可以反映岩石衰减蠕变过程特点,同时也可反映岩石蠕变的瞬时变形特性.
4)该模型仅有5个模型参数,即E0,E1,η,α和tF,较现有同类模型的参数少.
综合上述可知,本文建立的岩石蠕变模型即式(17)较现有同类模型具有明显的优越性.当然,本文模型与实际的吻合程度尚需工程实例进行验证,同时,还需解决本文模型参数的确定方法问题,下面将作详细介绍.
3 岩石蠕变模型的参数确定方法
前面已建立出模拟岩石蠕变全过程的蠕变模型,其包含5个模型参数即E0,tF,α,E1和η,参数的确定方法是岩石蠕变模型研究不可或缺的重要研究内容,目前确定岩石蠕变模型参数的方法大多采用基于试验曲线的曲线拟合或反演的确定方法,该方法虽然可行,但是分析过程复杂,参数物理意义也不很明确,使其工程应用受到限制.因此,有必要探讨更为简单实用的岩石蠕变模型参数确定方法.
3.1 蠕变寿命tF的确定方法
岩石蠕变寿命是指岩石蠕变破坏的时间,在岩石发生蠕变破坏时,岩石的应变率趋于无穷大,也就是说岩石蠕变寿命tF是岩石蠕变曲线的垂直渐近线所对应的蠕变时间,如图1所示,因此,根据岩石蠕变试验曲线可以较容易确定出tF.
3.2 弹性模量E0的确定
由图1可知,在应力σ0作用下,蠕变试验曲线的起始点(当t=0时)存在瞬时应变ε0,近似假定其为弹性应变,于是,弹性模量E0可由式(1)确定.
3.3 参数α的确定方法
根据前述对于岩石蠕变过程与机理的分析可知,当岩石进入加速蠕变阶段之后,黏弹性变形已基本稳定,随时间增长的只是永久变形.因此,由本文建立的岩石蠕变模型即式(17)可知,在加速蠕变段,岩石总蠕变即为弹塑性损伤体所表示的变形与Kelvin体所表示的黏弹性变形稳定值之和,而黏弹性变形稳定值可通过式(3)取极限求得,即:
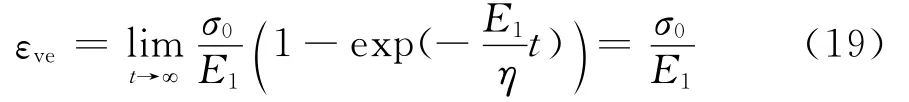
于是,如果在加速蠕变阶段试验曲线上取一点(ti,εi),则:
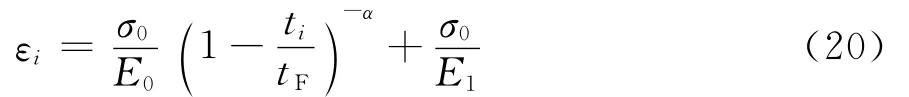
同样,在加速蠕变阶段试验曲线上另取一点(tj,εj),则:
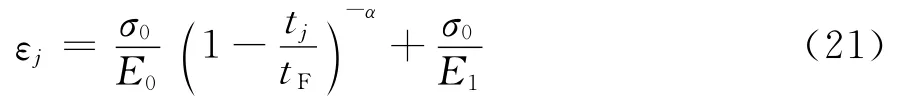
于是由式(20)及(21)可得:
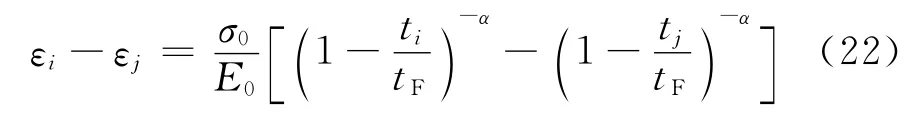
因此,由式(23)即可确定出模型参数α.
3.4 黏弹性参数E1,η的确定方法
由前述分析可知,加速蠕变阶段蠕变可近似采用式(20)或(21)进行分析,因此,如果在加速蠕变段取n个试验点(ti,εi)(i=1,2,…,n),对于每个试验点可由式(20)或(21)计算出相应的黏弹性模量E1i:

取上述E1i的平均值作为黏弹性模量E1:

在加速蠕变段之前曲线上取n个试验点(ti,εi)(i=1,2,…,n),必然满足式(17),即:

于是可得相应的黏滞系数ηi:
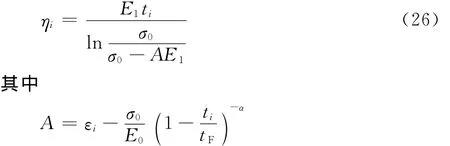
取ηi的平均值作为黏滞系数η:

4 工程实例分析与模型验证
为了探讨本文岩石蠕变模型的合理性与可行性,引入文献[13]中软岩和文献[9]中硬岩的蠕变试验资料进行分析,据此采用本文方法确定出模型参数如表1所示,于是可得到本文的理论曲线,并与试验曲线进行比较分析,如图4~图6所示,由此可以看出,本文模型的模拟效果良好.
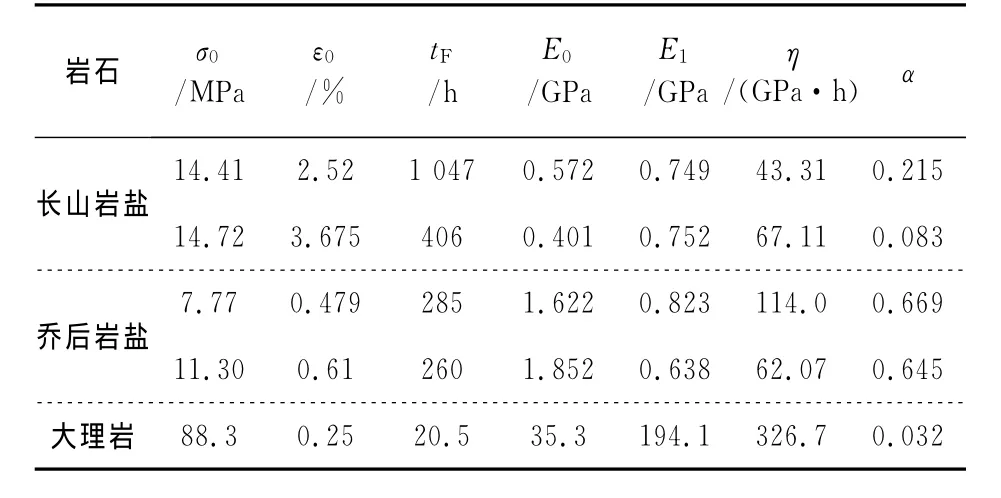
表1 岩石蠕变模型参数Tab.1 The parameters of rock creep model

图4 长山岩盐蠕变实测与理论曲线Fig.4 Test and theoretical creep curves of Changshan rock

图5 乔后岩盐蠕变实测与理论曲线Fig.5 Test and theoretical creep curves of Qiaohou rock
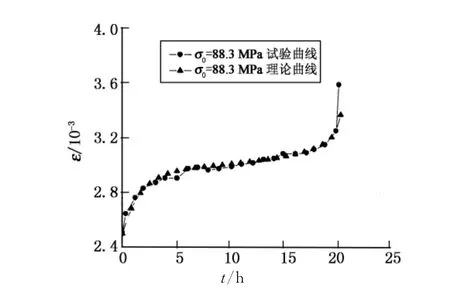
图6 大理岩蠕变实测与理论曲线Fig.6 Test and theoretical creep curves of marble
5 结 论
本文在深入研究岩石蠕变机理及蠕变过程阶段性特征的基础上,将岩石蠕变视为线性与非线性蠕变的迭加,以Kelvin体模型反映岩石的线性蠕变过程即减速蠕变过程,引入损伤理论,构建出了弹塑性损伤体元件模型,以此反映岩石的非线性流变过程即加速蠕变过程,从而对岩石蠕变全过程尤其是加速蠕变过程模拟方法进行了深入研究,由此可得如下结论:
1)建立出了反映岩石蠕变全过程特征的岩石蠕变模型,它不仅可以较好地模拟减速蠕变过程,同时,还可以较好地模拟加速蠕变过程.
2)提出了简单可行的岩石蠕变模型参数确定方法,该模型仅有5个模型参数,模型参数少.
3)理论与实测曲线对比分析表明了本文模型的合理性与可行性.
[1] CHALLAMEL N,LANOS C,CASANDJIAN C.Creep damage modeling for quasi-brittle materials[J].European Journal of Mechanics-A/Solids,2005,24(4):593-613.
[2] ZHOU H,JIA Y,SHAO J F.A unified elastic-plastic and viscoplastic damage model for quasi-brittle rocks[J].International Journal of Rock Mechanics &Mining Sciences,2008,45:1237-1251.
[3] 贺如平,张强勇,王建洪,等.大岗山水电站坝区辉绿岩脉压缩蠕变试验研究[J].岩石力学与工程学报,2007,26(12):2495-2503.HE Ru-ping,ZHANG Qiang-yong,WANG Jian-hong,et al.Study on compressive creep test on diabasic dike at dam site of Dagangshan hydropower station[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(12):2495-2503.(In Chinese)
[4] 陈卫忠,谭贤君,吕森鹏,等.深部软岩大型三轴压缩流变试验及本构模型研究[J].岩石力学与工程学报,2009,28(9):1735-1744.CHEN Wei-zhong,TAN Xian-jun,LV Sen-peng,et al.Research on large-scale triaxial compressive rheological test of soft rock in depth and its constitutive model[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(9):1735-1744.(In Chinese)
[5] 蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2006.CAI Mei-feng,HE Man-chao,LIU Dong-yan.Rock mechanics and engineering[M].Beijing:Science Press,2006.(In Chinese)
[6] 袁海平,曹平,许万忠,等.岩石粘弹塑性本构关系及改进的Burgers蠕变模型[J].岩土工程学报,2006,28(6):796-799.YUAN Hai-ping,CAO Ping,XU Wang-zhong,et al.Viscoelasto-plastic constitutive relationship of rock and modified Burgers creep model[J].Chinese Journal of Geotechnical Engineering,2006,28(6):796-799.(In Chinese)
[7] 邓荣贵,周德培,张倬元,等.一种新的岩石流变模型[J].岩石力学与工程学报,2001,20(6):780-784.DENG Rong-gui,ZHOU De-pei,ZHANG Zhuo-yuan,et al.A new rheological model for rocks[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(6):780-784.(In Chinese)
[8] 朱昌星,阮怀宁,朱珍德,等.岩石非线性蠕变损伤模型的研究[J].岩土工程学报,2008,30(10):1510-1513.ZHU Chang-xing,RUAN Huai-ning,ZHU Zhen-de,et al.Nonlinear rheological damage of rock[J].Chinese Journal of Geotechnical Engineering,2008,30(10):1510-1513.(In Chinese)
[9] 佘成学.岩石非线性黏弹塑性蠕变模型研究[J].岩石力学与工程学报,2009,28(10):2006-2011.SHE Cheng-xue.Research on nonlinear viscoelasto-plastic creep model of rock[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):2006-2011.(In Chinese)
[10]范庆忠,高延法.软岩蠕变特性及非线性模型研究[J].岩石力学与工程学报,2007,26(2):391-397.FAN Qing-zhong,GAO Yan-fa.Study of nonlinear creep model of soft rock[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(2):391-397.(In Chinese)
[11]LEMAITRE J.How to use damage mechanics[J].Nuclear Engineering and Design,1984,80(3):233-245.
[12]KACHANOV M.Effective elastic properties of cracked sdids:cvitical review of some basic concepts[J].Applied Mechanics Review,1992,45(8):304-335.
[13]邱贤德,姜永东,阎宗岭,等.盐岩的蠕变损伤破坏分析[J].重庆大学学报,2003,26(5):106-109.QIU Xian-de,JIANG Yong-dong,YAN Zong-ling,et al.Creep damage failure of rock salt[J].Journal of Chongqin University,2003,26(5):106-109.(In Chinese)
