吉布斯函数判据的应用及讨论
2013-03-17秦萍路莹
秦萍,路莹
(1.信阳师范学院物理电子工程学院,河南信阳 464000;2.洛阳师范学院物理与电子信息学院,河南洛阳 471022)
吉布斯函数判据的应用及讨论
秦萍1,路莹2
(1.信阳师范学院物理电子工程学院,河南信阳 464000;2.洛阳师范学院物理与电子信息学院,河南洛阳 471022)
从吉布斯函数判据出发,推导出系统的平衡条件和平衡的稳定性条件,并应用吉布斯函数判据讨论了范德瓦尔斯等温气液相变.
平衡判据;平衡条件;平衡的稳定性条件
在一般的热力学统计物理教科书中,开放系统的平衡条件和平衡的稳定性条件大都是从熵判据出发来推导的[1-4].由于系统的内能与熵密切相连,所以应用内能判据推导系统的平衡稳定性条件也能见到[5].但应用其它判据的推导还没见过.文献[1]指出:熵判据是基本判据,它虽然只适用于孤立系统,但只要把参与变化的全部物体都包括在系统之内,原则上可以对各种热动平衡问题做出解答;同时指出:在实际应用上,对于经常遇到的物理条件,引入其它判据更为方便.在不同的条件下可以有不同的判据,如等温等容条件下有自由能判据、等温等压条件下有吉布斯函数判据、熵和体积不变条件下有内能判据等.本文从吉布斯函数判据出发来推导系统的平衡条件和平衡稳定性条件.并应用吉布斯函数判据讨论范德瓦尔斯等温气液相变.
1 吉布斯函数判据
吉布斯函数是以温度和压强为自然变量的状态函数,在温度和压强不变的条件下,系统中的不可逆过程总是朝着吉布斯函数减少的方向进行,达到平衡态时吉布斯函数最小.如果围绕某一状态发生各种虚变动引起的吉布斯函数变化ΔG>0,该状态的吉布斯函数就具有极小值.因此,在温度和压强不变的条件下,系统处在稳定平衡状态的必要和充分条件为ΔG>0,此即为吉布斯函数判据[1].
2 吉布斯函数判据的应用
2.1 推导系统的平衡条件和平衡的稳定性条件
把ΔG>0用泰勒级数展开并精确到二级近似:

在等温等压条件下,系统达到平衡时,吉布斯函数G达到极小值,这时内参量偏离平衡态的任何变动都会导致吉布斯函数G的变动恒大于0.因此可得到等温等压下的极值条件:

等温等压下的稳定性条件:

先由极值条件推导系统的相平衡条件和化学平衡条件.
假设存在一个由某种纯物质组成的两相孤立系统,内部等温等压.将两相设为α相和β相,现在选取某一相,它在受到外界干扰后有一极小变化,另一相也有相应的变化.
两相的吉布斯函数的一级变分分别是:δGα=μαδnα,δGβ=μβδnβ,即
2y32y4+y3y12+y4y12-y32y1-y32y2-2y12y2+3y1y2y3-3y1y3y4+y1y2y4-y2y3y4=0

因为系统孤立,故有:δn=δnα+δnβ=0,即δnα=-δnβ,故(μα-μβ)δnα=0,又物质的量变化是不为零的,所以可得

即两相的化学势相等,这就是相变平衡条件[1].
除了相平衡条件外,由吉布斯函数判据也可以很方便地推导出化学平衡条件.
设有一个由物质ABCD组成且可发生化学反应的恒温恒压的均相系统,其方程式为
其化学势分别为μAμBμCμD,在发生一个微小的变化后其吉布斯函数的变化为

平衡时有dG=0,而dξ≠0(是各组元变化的共同的比例因子).故有

这就是化学平衡条件.即产物的化学势与其系数的乘积之和等于反应物的化学势与其系数的乘积之和.
它们只是平衡的必要条件,不足以断定平衡是否稳定,要得到平衡状态的充分条件必须讨论吉布斯函数的二级变分.并且由此得到平衡的稳定条件.

由于媒质比子系统大得多,当子系统发生变化时,有δ2G0<<δ2G,系统的吉布斯函数变化主要取决于子系统,即≈δ2G>0,吉布斯函数的二级微分为

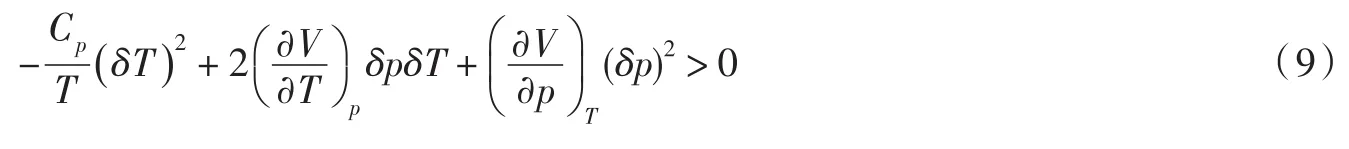
式(9)两边同时除以(δT)2得到




这与用熵判据推导出的平衡稳定性条件一致.这说明了吉布斯函数判据也是一个普适的判据.
2.2 讨论范德瓦尔斯气液相变
先求摩尔吉布斯函数的表达式,因为Gm=Fm+pVm,而F可由微分方程

积分得到




3 结束语
从吉布斯函数判据出发推导出了系统的平衡条件和平衡的稳定性条件,并用该判据讨论了范德瓦尔斯气液相变,扩展了思路,为用熵与内能以外的G判据研究系统的平衡及平衡的稳定性提供有益的参考.对学习者理解平衡判据,应用平衡判据提供了理论依据.

图1 Vm-p与Gm-p曲线的比较
[1]汪志诚.热力学与统计物理[M].北京:高等教育出版社,2008:78-79.
[2]王竹溪.热力学[M].北京:北京大学出版社,1955:292-293.
[3]薛增泉.热力学与统计物理[M].北京:北京大学出版社,2000:34-35.
[4]马本堃,高尚慧,孙煜.热力学与统计物理[M].北京:高等教育出版社,1988:91-92.
[5]龚昌德.热力学与统计物理[M].北京:高等教育出版社,1982:58-60.
[6]张弛.不等式[M].上海:上海教育出版社,1963:35-36.
[7]倪华,田立新.Bellman不等式的推广及其应用[J].信阳师范学院学报:自然科学版,2010,23(2):165-168.
[8]胡颉,佘守光.范德瓦尔斯汽液状态方程纵横谈[J].大学物理,2005,24(10):15-20.
[9]潘海民,马宝红,路莹.不可逆过程进行速率问题的数学模型及应用[J].常熟理工学院学报,2009,23(4):34-38.
The Application of and Discussion about Gibbs Function Criterion
QIN Ping1,LU Ying2
(1.College of Physics and Electronic Engineering,Xinyang Normal University,Xinyang 464000,China; 2.College of Physics and Electronic Information Physics,Luoyang Normal College,Luoyang 471022,China)
On the basis of Gibbs function criterion,the authors of this paper deduced the equilibrium condition and the balance stable condition of homogeneous system,and discussed the van der Waals isothermal gas liquid phase transition by means of Gibbs function criterion.
Gibbs function criterion;equilibrium condition;stability condition of equilibrium
O414.13
A
1008-2794(2013)04-0035-04
2013-03-30
河南省教育厅自然科学基金资助项目(2010B140010)
秦萍,副教授,研究方向:凝聚态物理,E-mail:xywuliqin@126.com.
