满映射Logistic数字混沌序列的产生及性能分析❋

余金峰，杨文革，路伟涛，王金宝

（1.装备学院光电装备系，北京101416；2.洛阳电子装备试验中心，河南洛阳471003）

满映射Logistic数字混沌序列的产生及性能分析❋

余金峰1，2，❋❋，杨文革1，路伟涛1，王金宝1

（1.装备学院光电装备系，北京101416；2.洛阳电子装备试验中心，河南洛阳471003）

Logistic映射形式简单，但表现出了复杂的动态性能。以满映射Logistic混沌序列为对象，讨论了混沌序列数字化的两种方法，推导了数字混沌序列比特位分布概率，计算了截短数字混沌序列的相关性能。结果表明，在不变分布偶对称的情况下，两种方法得到的数字化混沌序列都是“0”“1”等概率的，截短序列的自相关函数旁瓣方差和互相关方差均等于序列长度N的倒数。对数字化Logistic混沌序列进行了数值仿真，所得结果与结论相吻合；仿真结果还显示，自相关旁瓣和互相关均服从高斯分布。研究结果使得能够从理论上对一类数字混沌序列的特性进行整体把握，超越了经验性的结论，便于在有关系统中进行应用分析。

Logistic映射；混沌序列；数字化；扩频序列；相关特性

1 引言

在扩频通信领域，通常采用的扩频序列有m序列或Gold序列等伪随机噪声序列（PRN），它们是由多级移位寄存器或其他延迟元件通过线性反馈产生的。这些序列性能良好，满足了一般扩频系统的需要。但在实用中也存在着一些不足，比如，序列的长度不能任意选取，序列的数量有限，序列的复杂度不高等。

混沌现象是在非线性动态系统中出现的确定性的、类似随机的过程，这种过程既非周期，又不收敛，并且对初始值有极其敏感的依赖性［1］。混沌信号的这种类随机特性十分适合于通信中的噪声伪装调制，并且通过混沌系统对初始值的依赖性，可以提供数量众多、非相关、类随机而又确定可以再生的信号［2］。所以，随着混沌理论研究的深入，人们希望它能够成为产生扩频序列的新的来源。

目前，人们已经大量研究了Logistic等多种非线性映射产生混沌扩频序列的方法，并对其统计特性进行了分析［2－10］。为了利用混沌序列良好的相关特性，Heidari-Bateni等人［2－3］提出了将混沌序列用作扩频序列的思想，并给出了用混沌实值序列构建扩频通信系统的方法，同时指出，数字化混沌序列同样具有性能良好的相关特性。混沌序列的数字化方法除了二值量化法之外，文献［4－6］中给出了多比特量化法，并将数字混沌序列用作扩频通信系统的扩频序列。对截短数字混沌序列的相关特性，文献［7－9］中给出了经验性结论，是拟合得到的结果。对数字混沌序列相关特性缺少理论上的解析式结论，这对于混沌序列特性的整体把握以及有关应用的理论分析是不利的。

本文以满映射Logistic为对象，讨论了二值量化法和多比特量化法两种实现实值序列数字化的方法；对于不变分布具有对称性的混沌映射，对由其产生的数字混沌序列的比特位分布概率进行了理论分析；推导了截短数字序列相关函数的均值和方差；并对有关结论进行了数值仿真和验证。

2 Logistic映射

Logistic映射是实际系统中存在的最简单的非线性差分方程，是一个被广泛研究的动态系统，能够表现出复杂的动态行为。其映射方程为

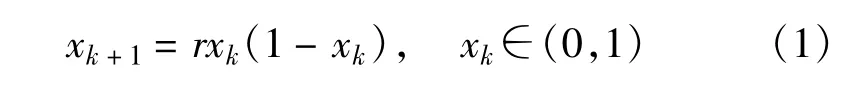
研究表明，Logistic映射的动态行为与分形参数r密切相关，随着r的变化，Logistic映射可以呈现出周期性或混沌态。具体地讲，当0≤r≤3.569 945 6≅rc时，序列{x}k呈现出周期为2m（m为正整数）的周期性；当rc＜r≤4时，Logistic映射处于混沌状态，此时由Logistic映射产生的序列{x}k非周期、不收敛、对初始值极其敏感。

r＝4时，Logistic映射的输入值和输出值都在（0，1）区间，称为满映射。在这种情况下不用对映射的初始值进行选择（少数稳定点除外）。因此，选择分形参数r＝4时的Logistic映射进行研究讨论。

混沌具有类随机性，可以用概率统计方法定量分析混沌序列的特性。Schuster H.G［1］证明了式（2）所产生的混沌序列{xk：k＝0，1，2…}的不变测度函数为

ρ（x）不依赖于初始值x0，所以式（2）表达的系统具有遍历性。

由不变测度函数，可以计算得到序列的如下数字特征［4］，即序列的均值¯x和序列的自相关函数Rac（m）：

独立选取两个初始值x10以及x20，若迭代产生的两条轨迹无位移重叠，则序列互相关为

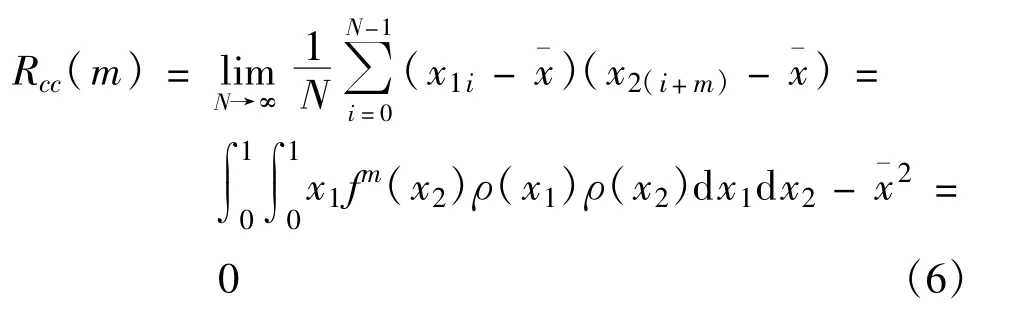
以上性质说明，映射（2）生成的序列具有良好的相关性能。

3 实值混沌序列数字化的方法

用于扩频的混沌序列常用的有两种形式，分别是实值序列和数字序列。实值序列就是把混沌映射的轨迹{xk：k＝0，1，2…}直接作为扩频序列。由于序列元素是（0，1）区间上的模拟量，不便于数字手段传输，所以，通常将实值序列进行数字化，使之适合实现数字传输。将实值序列数字化的方法有两种，分别是二值量化法和多比特量化法［6－7］。

二值量化法，就是将每一个实值序列元素xk进行0、1二值量化，得到序列{ak：k＝0，1，2…}。对于r＝4的Logistic映射，均值为0.5，其二值量化规则为

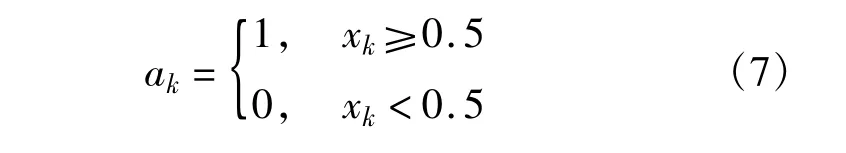
二值量化法虽然实现了实值序列的数字化，但每个实值序列元素只能得到一个比特数值。而多比特量化法则是对每一个实值序列元素进行L位的二进制量化，相对于二值量化，在得到相同长度的数字序列时，迭代计算量要降低L倍。多比特量化的规则为如下。

把区间（0，1）上的小数x写成二进制数表达形式：

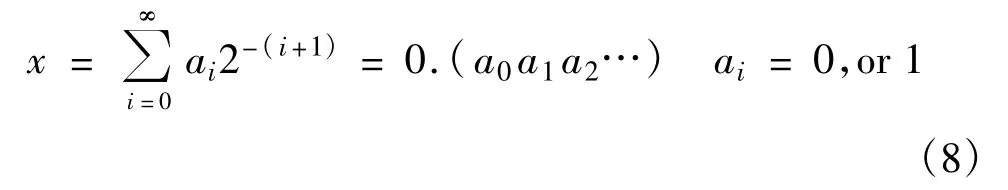
取前L位表示x，舍弃后面的位，则

提取2－L，将上式变为

其中，X是一个由L位的二进制数表示的整数，它与小数x之间存在一一对应关系，可以把X看作是对x进行多比特量化的结果。把xk和xk＋1都写成如上的形式，代入映射公式（2），可得

这样每迭代一次产生一个Xk，相应地可得到L位二进制比特。

4 数字混沌序列的随机性分析

由分形参数为4时混沌序列的不变测度函数可知，ρ（x）关于x＝0.5偶对称：

根据这一特性，可以得到数字化序列元素的分布特性［5］。由上式可得

在L比特的任意位置i出现“0”的概率为

也就是，在多比特量化数字序列的任意位置上，出现“0”和“1”的概率相等。

所以，对于满映射Logistic序列来说，其不变测度在（0，1）区间上关于0.5偶对称，其数字化序列的任意位上出现“0”或“1”的概率相等，数字化后的混沌序列为随机序列。事实上，如果映射的不变测度具有对称性，那么，将其对称轴进行变换后，通过多比特量化方法所得到的数字序列，其任意位上同样是“0”、“1”等概率的，可以看作随机序列。

5 截短数字混沌序列的相关特性

混沌序列的非周期性是在理论上计算数值无限精度的情况下理想特性。而在实用中，由于计算精度总是有限的，映射的状态数目就总是有限的，从这个意义上说得到的序列必然呈现周期性。计算精度越高，序列的周期会越长。当计算精度较高、周期较长时，可以把序列近似看作非周期的。

尽管混沌序列是非周期的，实用中多采用有限长序列。把混沌信号作为一种序列的新来源，对混沌序列按照需要进行截短，把截短的混沌序列作为扩频序列使用。截短的方法有两种，一是对单个混沌序列按顺序截取成段，二是用不同的初始值迭代出不同的序列。我们假设，无论哪种方法，截取出的序列都是长度为N的序列。同时，序列的元素ai已由原来的“1”和“0”转换成了“1”和“－1”。下面计算截短序列的特性与长度N之间的关系［11］。

自相关函数为

序列的元素ai是“1”和“－1”等概率的，其均值为0。元素ai的取值与其他元素的取值没有关系，所以各元素是独立的。由此可计算自相关函数的均值为

则其自相关函数的均值和方差分别为

6 数值仿真与结论验证

前面得到了数字混沌序列自相关函数和互相关函数的均值和方差，下面进行数值验证。由于序列的不变测度与初始值无关，序列具有遍历性，所以可以用时间相关代替统计相关。

取两个初值分别为x01＝0.345和x02＝0.456，序列长度N＝1 024。计算实值序列、二值量化序列和多比特量化序列的自相关和互相关函数，并计算自相关旁瓣和互相关的均值和方差如表1所示。为突出序列长度的作用，采用不作归一化的相关函数。可以看出，自相关旁瓣和互相关的均值接近于0，数字序列自相关旁瓣和互相关的方差约等于序列长度N。

表1 自相关旁瓣和互相关的均值和方差Table 1 Themean and variance of correlations

将实值序列、二值量化序列和多比特量化序列的自相关和互相关函数作图，并对自相关函数旁瓣和互相关函数作直方图，为进行比较，同时给出了正态分布N（0，N）的概率密度曲线，见图1～5。可以看出，3种序列的自相关函数都与冲激函数相似，自相关旁瓣和互相关与噪声相似。

图1 实值序列的相关函数Fig.1 The correlation of analog sequence

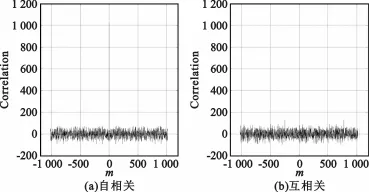
图2 二值量化序列的相关函数Fig.2 The correlation of two-value quantified sequence

图3 多比特量化序列的相关函数Fig.3 The correlation ofmulti-bitquantified sequence

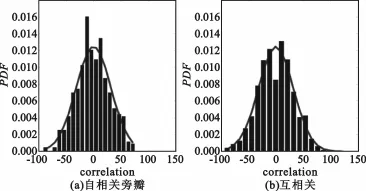
图4 二值量化序列相关函数分布特性Fig.4 The correlations distribution of two-valued quantified sequence

图5 多比特量化序列相关函数分布特性Fig.5 The correlation distribution ofmulti-bit quantified sequence

由数字序列的相关函数的分布特性可以看出，自相关函数旁瓣和互相关函数与均值为0方差为N的高斯分布基本吻合。

为检查自相关旁瓣和互相关函数的方差与序列长度N之间的关系，取两个初值分别为x01＝0.345和x02＝0.456，序列长度N为256、512、1 024、2 048、4 096，计算二值量化序列和多比特量化序列的自相关旁瓣方差和互相关函数方差，结果如图6所示。

图6 序列自相关函数旁瓣和互相关方差随N的变化Fig.6 The variation of correlation variance with sequence length N

可以看出，数字序列的自相关旁瓣方差和互相关函数方差约等于序列长度N，与前文给出的理论计算结果相一致。

7结束语

利用混沌映射产生扩频序列，只需要确定性映射方程和映射初始值即可。混沌映射可以提供数量众多，非周期、复杂度高的序列，已成为产生扩频序列的新的途径。对Logistic映射来说，得到相同长度序列时，多比特量化法比二值量化法需要更少的迭代运算量。混沌映射的不变分布具有对称性（满映射Logistic属于此类）时，两种数字化方法得到的数字序列都是“0”、“1”分布等概率的。对数字混沌序列进行截短利用时，自相关函数的均值为单位序列，互相关函数的均值为0；序列的自相关函数旁瓣方差和互相关函数方差约等于序列长度N的倒数。数值仿真的结果与文中理论计算结果相吻合。数值仿真结果还表明，序列的自相关函数旁瓣和互相关函数服从均值为0方差为1/N的高斯分布。本文的结果使得能够从理论上对一类数字混沌序列的特性进行整体把握，超越了经验性的结论，便于在有关应用中进行理论分析，同时对于其他混沌映射同样具有参考意义。

［1］Schuster H G.Deterministic chaos，an introduction（Second Revised Edition）［M］.Federal Republic of Germany：VCH，1988：37－69.

［2］Heidari-Bateni G，McGillem C D.Chaotic sequences for spread spectrum：an alternative to PN-sequences［C］//Proceedings of 1992 IEEE International Conference on Selected Topics in Wireless Communications.Vancouver，BC：IEEE，1992：437－440.

［3］Heidari-BateniG，McGillem C D.A chaotic direct-sequence spread spectrum communication system［J］.IEEETransactions on Communications，1994，42（2/3/4）：1524－1527.

［4］于银辉.混沌扩频通信技术研究与应用［D］.吉林：吉林大学，2005：22－24. YU Yin-hui.Study on chaotic spread spectrum communication technology and its application［D］.Jilin：Jilin University，2005：22－24.（in Chinese）

［5］王亥，胡健栋.数字混沌扩频通信系统［J］.北京邮电大学学报，1998，21（4）：8－11. Wang Hai，Hu Jiandong.Digital chaotic spread spectrum communication system［J］.Journal of Beijing University of Posts and Telecommunications，1998，21（4）：8－11.（in Chinese）

［6］柳平，闫川，黄显高.改进的基于Logistic映射混沌扩频序列的产生方法［J］.通信学报，2007，28（2）：134－140. LIU Ping，YAN Chuan，HUANG Xian-gao.Optimized methodof generating the spread-spectrum sequences based on Logistic-map［J］.Journal on Communications，2007，28（2）：134－140.（in Chinese）

［7］王亥，胡健栋.Logistic-Map混沌扩频序列［J］.电子学报，1997，25（1）：19－24. WANG Hai，HU Jian-dong.Logistic-map chaotic spread spectrum sequence［J］.ACTA Electronica Sinica，1997，25（1）：19－24.（in Chinese）

［8］胡文立，王玫.Logistic数字混沌序列的性能分析［J］.桂林电子工业学院学报，2001，21（1）：26－29. HU Wen-li，WANG Mei.The correlation property of digital chaotic sequence by Logisticmaps［J］.Journal of Guilin Institute of Electronic Technology，2001，21（1）：26－29.（in Chinese）

［9］蔡国权，宋国文，余大鹏.Logistic映射混沌扩频序列的性能分析［J］.通信学报，2000，21（1）：60－63. CAIGuo-quan，SONG Guo-wen，YU Da-peng.On properties of Logistic-map chaotic spread spectrum sequences［J］.Journal on Communications，2000，21（1）：60－63.（in Chinese）

［10］朱志良，吴艳芹，刘向东，等.中间多比特量化混沌扩频序列及其性能分析［J］.东北大学学报，2002，23（8）：733－737. ZHU Zhi-liang，WU Yan-qin，LIU Xiang-dong，et al. Chaotic spread spectrum sequence bymid multi-bite quantifying and its properties［J］.Journal of Northeastern University，2002，23（8）：733－737.（in Chinese）

［11］Misra P，Enge P.全球定位系统－信号、测量与性能［M］.罗鸣，曹冲，肖雄兵，等，译.北京：电子工业出版社，2008：277－279. Misra P，Enge P.Global Positioning System Signals，Measurements，and Performance［M］.Translated by LUO Ming，CAO Chong，XIAO Xiong-bing，et al.Beijing：Publishing House of Electronics Industry，2008：277－279.（in Chinese）

余金峰（1969—），男，河南唐河人，2001年于国防科技大学获硕士学位，现为博士研究生，主要研究方向为航天器测量与控制；

YU Jin-feng was born in Tanghe，Henan Province，in 1969.He received the M.S.degree from National University of Defense Technology in 2001.He is currently working toward the Ph.D. degree.His research interests include spacecraft TT＆C，spread spectrum system.

Email：yujinfeng2008＠sohu.com

杨文革（1966—），男，江西金溪人，2000年于北京理工大学获博士学位，现为教授、博士生导师，主要研究方向为航天测量与控制、雷达信号处理；

YANGWen-ge was born in Jinxi，Jiangxi Province，in 1966. He received the Ph.D.degree from Beijing Institute of Technology in 2000.He isnow a professor and also the Ph.D.supervisior.His research interests include TT＆C and radar signal processing.

路伟涛（1985—），男，河南西华人，2010年于装备指挥技术学院获硕士学位，现为博士研究生，主要研究方向为航天测控、扩频技术；

LUWei-taowas born in Xihua，Henan Province，in 1985.He received theM.S.degree from Institute of Command and Equipment in 2010.He is currently working toward the Ph.D.degree.His research interests include TT＆C，spread spectrum system.

王金宝（1980—），男，河北衡水人，2009年于装备指挥技术学院获得硕士学位，现为博士研究生，主要研究方向为航天测控、扩频技术。

WANG Jin-bao was born in Hengshui，Hebei Province，in 1980.He received the M.S.degree from Institute of Command and Equipment in 2009.He is currently working toward the Ph.D.degree.His research interests include TT＆C，spread spectrum system.

Generation and Performance Analysis of Digital Chaotic Sequence from Surjective Logistic-M ap

YU Jin-feng1，2，YANGWen-ge1，LUWei-tao1，WANG Jin-bao1
（1.Departmentof Optical and Electrical Equipment，Academy of Equipment，Beijing 101416，China；2.Luoyang Electronic Equipment Test Centre，Luoyang 471003，China）

Logistic-Map is a widely studied typical discrete time non-linear dynamic system.Based on the surjective Logistic-Map，this paper discusses twomethods to digitalize chaotic sequences，induces the statistical properties of the occurrence of“0”and“1”of the digital chaotic sequences，and investigates the correlation characteristicsof the cut-down sequences.The result shows：“0”and”1”have equal probabilities in digital chaotic sequences generated by both digitalization methods when amap has symmetrical invariant distribution；the variance of correlation equals to the reciprocal of sequence length N.The theoretical conclusions are verified by numerical simulations based on surjective Logistic-Map.The simulations result also shows the correlation obeys Gauss distribution.The theorical conclusions in this paper，rather than experiential formulars，are helpful to understand the correlation properties of digital chaotic sequences.

Logistic-Map；chaotic sequences；digitization；spread-spectrum sequences；correlation property

TN911；TN914.4

A

1001－893X（2013）02－0140－06

10.3969/j.issn.1001－893x.2013.02.006

2012－08－01；

2012－12－12 Received date：2012－08－01；Revised date：2012－12－12

❋❋通讯作者：Email：lwteecspku＠126.com Corresponding author：Email：lwteecspku＠126.com