扩频码PSO优化分配降低MC-CDMA信号峰均比❋
2013-03-17胡茂凯陈西宏薛伦生黄荣华
胡茂凯,陈西宏,薛伦生,黄荣华
(1.空军工程大学防空反导学院,西安710051;2.解放军第95100部队,广州510000)
扩频码PSO优化分配降低MC-CDMA信号峰均比❋
胡茂凯1,❋❋,陈西宏1,薛伦生1,黄荣华2
(1.空军工程大学防空反导学院,西安710051;2.解放军第95100部队,广州510000)
高峰均比(PAPR)是多载波码分多址(MC-CDMA)技术应用中亟待解决的关键问题。对于采用Walsh-Hadamard(WH)扩频码的系统来说,优化用户扩频码的分配方案可降低系统的PAPR,但最优扩频码分配方法运算复杂度太高。为此,采用具有优良迭代寻优能力的粒子群优化算法(PSO)来降低算法的复杂度。改进算法将最优分配方案的高维搜索问题转化为粒子群迭代寻优过程。分析比较和仿真结果表明,与最优算法相比,改进算法在降低PAPR性能方面有0.5~1.5 dB的性能损失,而复杂度远小于最优算法,是一种简单实用的峰均比降低方法。
多载波码分多址;扩频码分配;峰均比;粒子群优化算法
1 引言
多载波码分多址(Multicarrier Code Division Multiple Access,MC-CDMA)技术是正交频分复用(OFDM)技术与码分多址(CDMA)技术相结合的技术,兼有OFDM和CDMA的优点[1],被认为是未来无线通信领域最合适的方案之一。但MC-CDMA信号的具有高峰均比(Peak-to-Average Power Ratio,PAPR)特性。高峰均比信号往往会超出系统功率放大器(HPA)的线性范围,产生信号失真,导致系统性能的降低,因此必须设法降低MC-CDMA系统的PAPR。
MC-CDMA系统的峰均功率比和分配给用户的扩频序列密切相关,当采用Walsh-Hadamard(简称WH)扩频码时尤为显著,因此可以研究扩频码的优化分配方案来降低系统的PAPR[2-7]。文献[5-6]研究了采用WH扩频序列的MC-CDMA系统,证实当系统在线用户数目较少时,WH扩频码的选择对系统峰均比具有较大的影响;文献[7]详细分析了MC-CDMA信号的统计特性,并给出了峰均比的数学统计描述,并在此基础上研究了一种具有低复杂度的扩频码分配方案来降低信号的峰均比,与最优分配方案相比有一定的性能损失。事实上,降低峰均比能力和方法运算复杂度两个方面是相互矛盾的,最优的扩频码分配方案的获得需要付出很高的运算量。为此,本文将具有优良迭代寻优能力的粒子群优化算法(Particle Swarm Optimization,PSO)用于对扩频码分配优化方案的搜索来降低MC-CDMA系统峰均比,分析了MC-CDMA系统用户数目对信号PAPR的影响,然后详细描述了提出算法,最后对算法降低PAPR性能进行了仿真分析。
2 MC-CDMA信号的峰均比
图1所示为MC-CDMA下行链路发射机模型[7-8]。

图1 MC-CDMA发射端框图Fig.1 MC-CDMA transmittermodel

其中,Ts为MC-CDMA信号的符号周期。为了准确地描述信号的PAPR,一般要求对信号作过采样处理,当过采样因子L=4时,离散信号与连续信号的PAPR基本相同。式(1)对应的离散时域发射信号为
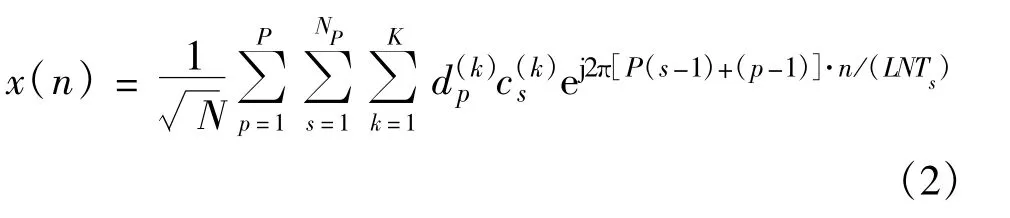
其中,n=0,1,…,LN-1。经过采样后的发射信号为x=[x0,x1,…,xLN-1]T。信号的峰均比PAPR定义为

式中,E{·}为求均值。常采用互补累积函数(CCDF),即一帧OFDM符号的PAPR值超过门限值PAPR0的概率来表征信号的PAPR性能:
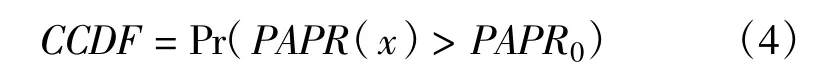
MC-CDMA系统中,扩频码的选择对系统的PAPR有较大影响。在二进制扩频码序列中,全为+1或-1的序列,以及+1和-1交替出现的序列,有最大的相关值,这些序列会使系统产生很大的PAPR。而WH序列就是如此。WH扩频序列具有良好的自相关和互相关特性,加上其简单的编码方式,近年来,很多文献都用WH码作为MC-CDMA系统的下行链路扩频码。它的循环构造方式为
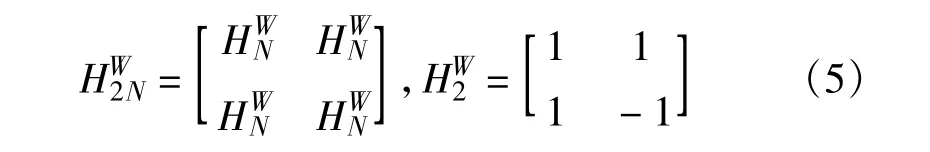
对于单用户以及用户数K较小时,信号的PAPR会变得很大。不过,当K较小时,可以通过对用户扩频码的合理选择和分配来降低信号的PAPR[5]。
通过对扩频码实现最优分配,可有效降低信号PAPR,但最优分配方法的运算量太高,需要的搜索次数为

以Np=64、K=32的系统为例,搜索复杂度为109,必须设法降低算法的运算量。本文将具有优良迭代寻优能力的粒子群算法应用于对最优扩频码分配方案的搜索。
3 改进的扩频码分配方法
将PSO算法应用于用户扩频码分配的关键,一是扩频码分配方案数学模型的建立,二是寻求合适的表达方法,使PSO算法中的粒子与任务分配的解相对应。
3.1 扩频码分配及模型建立
设有Np个WH扩频序列Ni(i=1,2,…,Np),系统最多可支持的用户数目即为Np,但考虑Np>K的情况,将Np个扩频序列分配给K个不同的用户Kj(j=1,2,…,K),作变量cij:

扩频码分配的最终目的是使得信号的PAPR最小,因此系统的扩频码分配模型为

同时考虑到分配的约束条件:
(1)cij∈{0,1},i=1,2,…,N;j=1,2,…,K;
3.2 基于PSO的扩频码分配方法
PSO算法中,粒子的位置表示所求问题的解,粒子由速度决定其飞行的方向和大小,解的优劣程度由每个粒子的适应值大小决定,适应度函数则是依据求解问题的目标函数确定。粒子通过跟踪个体极值pbest和全局极值gbest来更新速度和位置[9]。在一个D维的搜索空间中,设有M个粒子组成一个种群,第i个粒子位置表示为
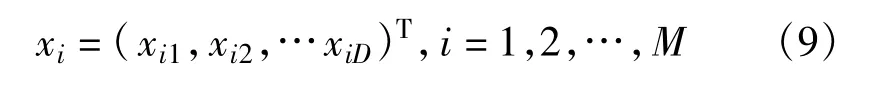
它对应于目标函数的一个潜在的解,而第i个粒子的飞行速度为

每个粒子经历过的最好位置(有最好的适应值或目标函数值)表示为

群体经历过的最好位置表示为
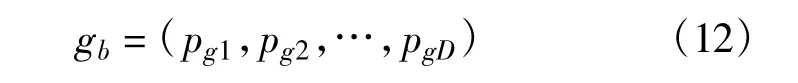
每个粒子通过跟踪个体极值和全局极值向最优解靠近,迭代过程中遵循以下基本公式:
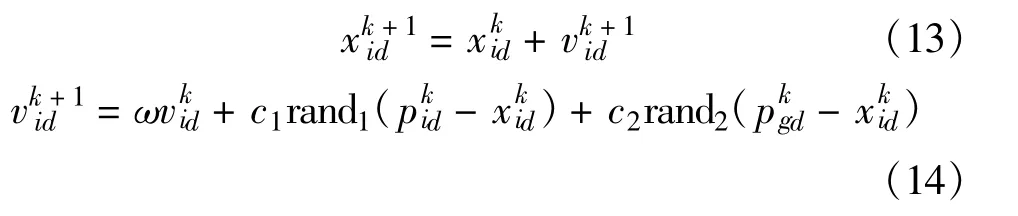
将PSO作为搜索最优扩频码分配方案的求解工具,系统任务分配的实质就是指派哪个扩频序列给哪个用户的问题,寻求合适的表达方法,使PSO算法中的粒子与任务分配的解相对应,是将PSO算法应用于扩频码分配的关键。
在粒子初始化过程中,粒子的维数应该等于系统在线用户的数目,这样粒子的位置即表示问题的一个潜在的解,另外,必须要满足3.1节中的3个约束条件,因此粒子在选择新位置时,不是在全定义域内进行选择。算法的具体步骤如下:
(1)定义搜索空间,即为备选的Np个扩频序列集合{Ni},将{Ni}映射为1~Np之间的整数;
(2)初始化粒子群体的位置和速度,取粒子维数D=K,每一维随机取1~Np之间的整数,且设置每一维位置量各不相同,即代表不同用户所分配的扩频序列不同,粒子速度向量v的每一维取-(Np-1)~(Np-1)之间的整数;
(3)初始化粒子的个体最优位置pbest及全局最优位置gbest,基于式(8)计算每个粒子的适应值,将当前各粒子的位置和适度值存储在各粒子的pbest中,将所有pbest中适度值最优个体的位置和适度值存储于gbest中;
(4)对于每个粒子,将其适应值与所经历的个体最优位置的适应值进行比较,若较好,则将其作为该粒子当前的最好位置;
(5)对于每个粒子,将其适应值与所经历的全局最好位置的适应值进行比较,若较好,则将其作为当前的全局最好位置;
(6)若满足收敛准则,进入步骤9,否则进入步骤7;
(7)根据式(13)~(14)生成下一代粒子,即生成新的扩频序列分配方案;
(8)计算当前粒子的适应值,并转入步骤4;
(9)搜索结束,输出最优粒子对应的扩频码分配方案及此时信号的PAPR。
4 仿真分析
首先分析扩频码分配方案对MC-CDMA信号峰均比的影响。图2为扩频码随机分配和最优分配下的系统PAPR性能,仿真时取P=4,Np=64,N=256,K=32,子载波映射为16-QAM。在多次随机分配方案中选择了4个具有代表性的仿真结果,由图可知,4次随机分配方案下的PAPR略有不同但差别不大,有1~2 dB不等的性能差异,而最优分配方案下的PAPR明显得到了降低。

图2 不同扩频码分配方案下的CCDF性能Fig.2 CCDF performance for different spread code allocation
下面对基于PSO优化的扩频码分配方法下的系统峰均比性能进行仿真分析,同时给出最优分配和随机分配时信号的PAPR曲线。仿真时设P=4,N=256,Np=64,K=8,子载波映射为16-QAM。设置粒子维数D=8,即与用户数目相等,最大迭代次数G=100,惯性系数ω=0.7,学习因子c1=c2=2,粒子群体个数M分别取20、50两种情况,仿真结果如图3所示。
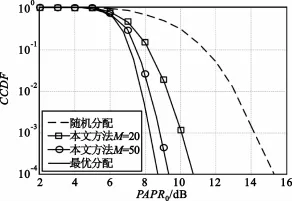
图3 改进扩频码分配方法下CCDF性能Fig.3 CCDF performance of proposed method
由图可见,扩频码优化分配均能有效降低MCCDMA信号的PAPR,当CCDF=10-3时,原信号的PAPR=14 dB左右,最优分配方法对应的PAPR=8.2 dB,而对于PSO扩频码分配算法,M=20时对应的PAPR为10 dB,M=50时对应的PAPR为8.7 dB,与最优分配方法相比分别有1.5 dB和0.5 dB的性能损失。而在运算复杂度方面,PSO算法设置的最大迭代次数为G=100次,远小于式(6)的运算量。
5 小结
当用户数目小于系统能支持的最大用户数目时,可以通过对扩频码的优化分配来降低MC-CDMA系统的峰均比。针对最优分配方法的高运算量,研究了一种基于粒子群优化的次优用户扩频码分配方法。分析与仿真结果表明,改进方法在PAPR降低能力上与传统的最优分配方法相近仅有0.5~1.5 dB的性能损失,而运算量得到了有效的降低,是一种简单实用的MC-CDMA系统峰均比降低方法。另外,本文方法还可与其他PAPR抑制方法结合使用,以更好地降低系统的峰均比。
[1]赵亚红,李伟华,吴伟陵.正交多载波调制(OFDM)技术及其应用[J].电讯技术,2001,41(1):92-95. ZHAO Ya-hong,LIWei-hua,WUWei-lin.OFDM Technology and Application[J].Telecommunication Engineering,2001,41(1):92-95.(in Chinese)
[2]Ginige T,Rajatheva N,Ahmed K M.Dynamic spreading code selection method for PAPR reduction in OFDM-CDMA systems with 4-QAM modulation[J].IEEE Communication Letters,2001,5(10):408-410.
[3]Shi Q,Latva-aho M.Simple spreading code allocation scheme for downlink MC-CDMA[J].Electronics Letters,2002,38(5):807-809.
[4]Yang L,Alsusa E.Dynamic code-allocation based PAPR reduction technique for MC-CDMA systems[C]//Proceedings of 2007 IEEEWireless Communications and Networking Conference.Hong Kong:IEEE,2007:628-633.
[5]OchiaiH,ImaiH.OFDM-CDMA with peak power reduction based on the spreading sequences[C]//Proceedings of 1998 IEEE International Conference on Communications.Atlanta,GA:IEEE,1998:1299-1303.
[6]HathiN,RodriguesM,Darwazeh I,etal.Analysis of the influence of Walsh-Hadamard code allocation strategies on the performance ofmulti-carrier cdma systems in the presence of HPA non-linearities[C]//Proceedings of 2002 Personal,Indoor and Mobile Radio Communications.Lisbon:IEEE,2002:1305-1309.
[7]Giannetti F,LotticiV,Stupia I.PAPR Analytical Characterization and Reduced-PAPR Code Allocation Strategy for MCCDMA Transmissions[J].IEEE Transactions on Wireless Communications,2011,10(1):219-227.
[8]Kang K,Kim S,Ahn D,et al.Efficient PAPR reduction scheme for satellite MC-CDMA systems[J].IEEProceedings of Communications,2005,152(5):697-702.
[9]刘斌,陈西宏,邓蕴昊.OFDM中基于粒子群优化的PTS相位因子优选算法[J].电测与仪表,2008(7):33-36. LIU Bin,CHEN Xi-hong,DENG Yun-hao.An optimal phase-factor selection algorithm for PTS based on PSO in OFDM[J].Electrical Measurement&Instrumentation,2008(7):33-36.(in Chinese)
作者简介:

胡茂凯(1985—),男,江苏沭阳人,2010年于空军工程大学获硕士学位,现为博士研究生,主要研究方向为多载波及扩频技术;
HU Mao-kai was born in Shuyang,Jiangsu Province,in 1985.He received the M.S.degree from Air Force Engineering University in 2010.He is currently working toward the Ph.D.degree.His research concernsmulti-carrier and spread spectrum communication.
Email:tgyxhmk@163.com
陈西宏(1961—),男,陕西西安人,2010年于空军工程大学获博士学位,现为教授、博士生导师,主要研究方向为导弹工程和通信技术;
CHEN Xi-hong was born in Xi′an,Shaanxi Province,in 1961. He received the Ph.D.degree from Air Force Engineering University in 2010.He is now a professor and also the Ph.D.supervisor. His research concernsmissile engineering and communication.
薛伦生(1972—),男,江苏东台人,2008年于空军工程大学获硕士学位,现为副教授、硕士生导师,主要研究方向为电子应用和通信技术;
XUE Lun-sheng was born in Dongtai,Jiangsu Province,in 1972.He received the M.S.degree from Air Force Engineering U-niversity in 2008.He is now an associate professor and also the instructor ofgraduate students.His research concerns electronic application and communication.
黄荣华(1984—),男,福建漳州人,2007年于空军工程大学获学士学位,现为助理工程师,主要研究方向为导弹发射工程和数据通信。
HUANG Rong-hua was born in Zhangzhou,Fujian Province,in 1984.He received the B.S.degree from Air Force Engineering University in 2007.He is now an assistant engineer.His research interests includemissile launch engineerin g and data transmission.
PSO-based Spreading Code Allocation for PAPR Reduction of MC-CDMA Signal
HUMao-kai1,CHEN Xi-hong1,XUE Lun-sheng1,HUANG Rong-hua2
(1.Air Defense&Antimissile Institute,Air Force Engineering University,Xi′an 710051,China;2.Unit95100 of PLA,Guangzhou 510000,China)
The high peak-to-average power ratio(PAPR)ofMulticarrier Code Division Multiple Access(MC-CDMA)is a key factor to be solved.In MC-CDMA system using Walsh-Hadamard(WH)spreading codes,the spreading code allocation is related to the PAPR and a reasonable allocation strategy can reduce signal PAPR. To reduce the high complexity of the optimal allocationmethod,particle swarm optimization(PSO)is introduced for seeking the optimum code allocation.Analysis and simulation results show that the proposed suboptimal method has a small performance loss(0.5~1.5 dB)in reducing PAPR.But the suboptimalmethod also has very low computational complexity and is suitable for practical system.
MC-CDMA;spread code allocation;PAPR;particle swarm optimization(PSO)
TN911
A
1001-893X(2013)02-0146-05
10.3969/j.issn.1001-893x.2013.02.007
2012-05-16;
2012-08-20 Received date:2012-05-16;Revised date:2012-08-20
❋❋通讯作者:tgyxhmk@163.com Corresponding author:tgyxhmk@163.com
