一种任意次非均匀B样条的细分算法
2013-03-16韩力文杨玉婷邱志宇
韩力文, 杨玉婷, 邱志宇
(1. 河北师范大学数学与信息科学学院,河北 石家庄 050024;2. 河北省计算数学与应用重点实验室,河北 石家庄 050024;3. 沙城中学,河北 张家口 075400)
一种任意次非均匀B样条的细分算法
韩力文1,2, 杨玉婷3, 邱志宇1
(1. 河北师范大学数学与信息科学学院,河北 石家庄 050024;2. 河北省计算数学与应用重点实验室,河北 石家庄 050024;3. 沙城中学,河北 张家口 075400)
类似于经典的、应用于任意次均匀B样条的Lane-Riesenfeld细分算法,提出了一种任意次非均匀 B样条的细分算法,算法包含加细和光滑两个步骤,可生成任意次非均匀B样条曲线。算法是基于于开花方法提出的,不同于以均匀B样条基函数的卷积公式为基础的 Lane-Riesenfeld细分算法。通过引入两个开花多项式,给出了算法正确性的详细证明。算法的时间复杂度优于经典的任意次均匀 B样条细分算法,与已有的任意次非均匀B样条细分算法的计算量相当。
计算机辅助几何设计;细分;开花;B样条;非均匀;节点插入
细分方法是简单高效的离散化几何造型方法,适用于任意拓扑结构,已在计算机辅助设计和计算机图形学界得到深入研究和广泛应用。大量细分方法是基于样条或是样条细分的推广。以B样条细分为例:1974 年Chaikin提出一种快速光滑曲线生成方法[1],即二次均匀B样条细分算法。1980年Lane和Riesenfeld将Chaikin算法推广到任意次 B样条细分上,提出任意次均匀 B样条细分算法[2]。Lane-Riesenfeld算法的第一步是加细,即双写控制顶点,第二步是光滑,即d层的中点平均,其中d是曲线次数,该算法为任意次均匀 B样条曲面细分方法[3-6]的研究提供了理论基础。Boehm和Cohen et al.分别给出了任意次非均匀节点插入算法,其中 Boehm节点插入算法[7]是在一个节点区间中插入一个节点,在均匀节点情况下 Boehm 算法的计算量低于Lane-Riesenfeld算法;Oslo算法[8]是在一个区间中同时插入多个节点,但是当进行细分时,我们只需要在每个连续的节点区间中插入一个新节点,此时Oslo算法退化为Boehm算法。
开花由Ramshaw[9]提出,现已成为研究样条理论的强有力工具,如样条理论中的升阶、降阶、细分算法、节点插入算法等都可以统一在开花这一工具下进行。2007年Vouga和Goldman给出了 Lane-Riesenfeld算法基于开花方法的两种证明[10],该方法比基于B样条基函数的连续卷积的标准证明[2]和基于de Boor算法的证明[11]更简单和容易理解。d次非均匀的B样条曲线细分也可以统一在开花方法下,如 2009年 Schaefer与Goldman 基于开花方法提出类似于Lane-Riesenfeld算法的任意次非均匀B样条曲线细分算法[12],以下称为Schaefer算法,该算法分为加细(双写控制顶点)和d层的非均匀光滑;2009年Cashman等基于开花方法,提出一种任意次对称的非均匀B样条细分算法[13],以下称为Cashman算法,该算法对于奇偶次算法有不同的细分规则,分为加细和层的非均匀光滑。本文基于开花方法提出一种任意次非均匀B样条的细分算法,该算法第一步为加细:双写控制顶点,第二步为层的非均匀光滑。通过引入两个开花多项式给出了该算法正确性的详细证明。
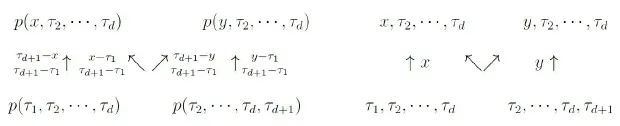
图1 开花的多仿射性质(左图)和等价意义下的简写(右图)
1 任意次非均匀B样条的细分算法
1.1 开花方法
本文算法是基于开花方法给出的,首先介绍开花的定义如下。
(1) 对称性:
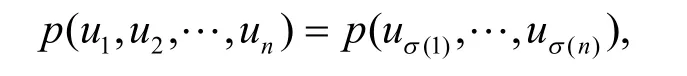
其中,σ是对{1,…,n}的任意置换。
(2) 多仿射性:
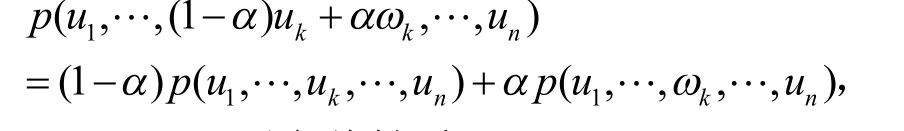
(3) 对角线性质:

1.2 任意次非均匀B样条的细分算法
B样条的开花多项式具有对偶泛函性质,即对于由节点向量τ决定的B样条P(t),第i个控制顶点Pi满足:。
给定两个开花多项式,若对应节点序列至多有一个不相同,则可利用多仿射性质实现节点x的插入,如下式:
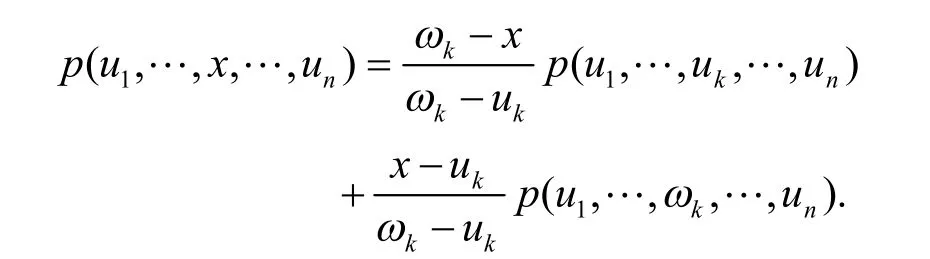
下面详细介绍任意次非均匀 B样条的细分算法,算法分为加细和光滑两步。
第1步是加细,即双写控制顶点。为了使最后得到的控制顶点的层数表示一致,将奇偶次加细后的控制顶点分别记为:… ,n,d为偶数;为奇数。
当 i≡ λ(mod 2)时:
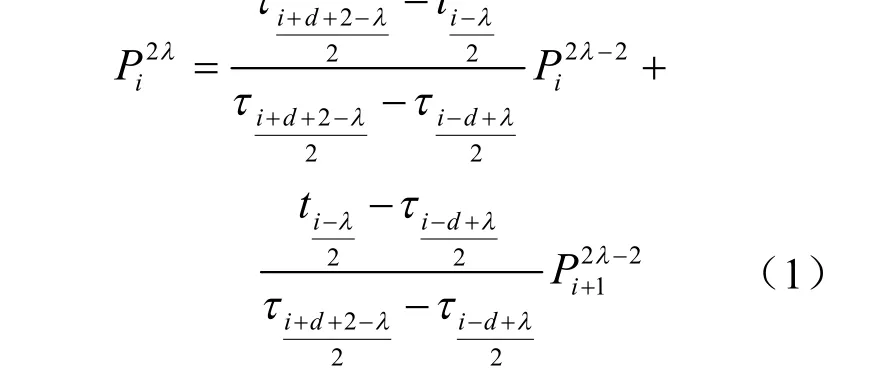
当 i- 1 ≡ λ(mod 2)时:

当 i≡ λ(mod 2)时:

当 i- 1 ≡ λ(mod 2)时:
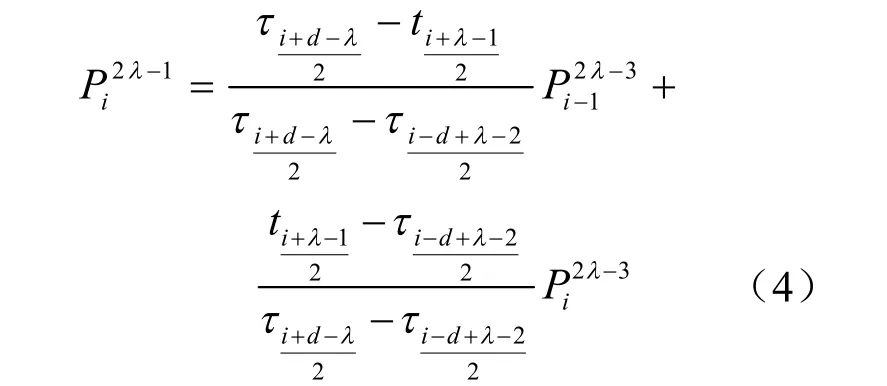


本文算法是任意次的非均匀 B样条细分算法,图2给出次数d=5和d=6的算法图示。算法包含两种类型的新顶点计算方法,一种是不经过计算直接将上一层的控制顶点作为下一层的控制顶点,如奇次算法最后一层中的双线箭头;另一种是由两个相邻的旧控制顶点经过多仿射组合得到下一层的新控制顶点。本文未考虑边界条件和重节点的影响。
2 算法正确性的证明
对于任意次数d,本文所提出的细分算法在细分过程中生成的控制顶点序列的极限为 d次的 B样条曲线。下面对于奇次的算法给出详细的证明。
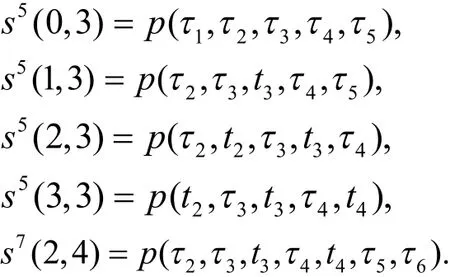
对于函数 rd(m , i),m个参数为插入节点,d-m个参数为初始节点,且要求。跟据靠近中心原则,将m个插入节点尽可能靠近中心的插入到初始节点向量中,并保证中心节点右侧的插入节点比中心节点左侧的插入节点多一个。若m为偶数,则中心节点为插入节点,若m为奇数,则中心节点为初始节点,例如:
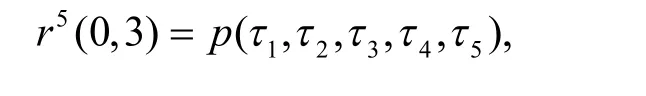


图2 次数 d= 5的B样条细分算法图示(a)和 d= 6的B样条细分算法图示(b)
引理 1对满足的奇数δ,第δ层的控制顶点满足:
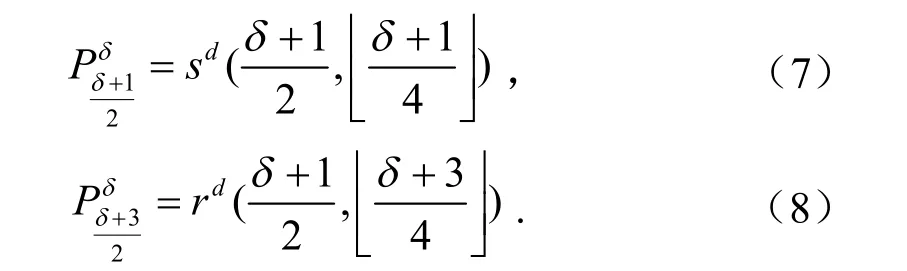
证明:若初始控制顶点为 n+1个,加细后为2 n+ 2个控制顶点。对于本文所提出的细分算法,当进行前层光滑操作时,每进行一层操作就减少2个控制顶点,层后剩余个控制顶点,且为偶数个。由本文算法可知,在层光滑操作后,其中一半的控制顶点的开花形式中的参数有个插入节点,形如函数另一半控制顶点的开花形式中的参数同样有个插入节点,形如函数
一般的,下标改变后,算法不变。故对于细分过程中控制顶点有以下结论成立:
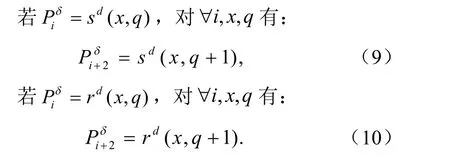
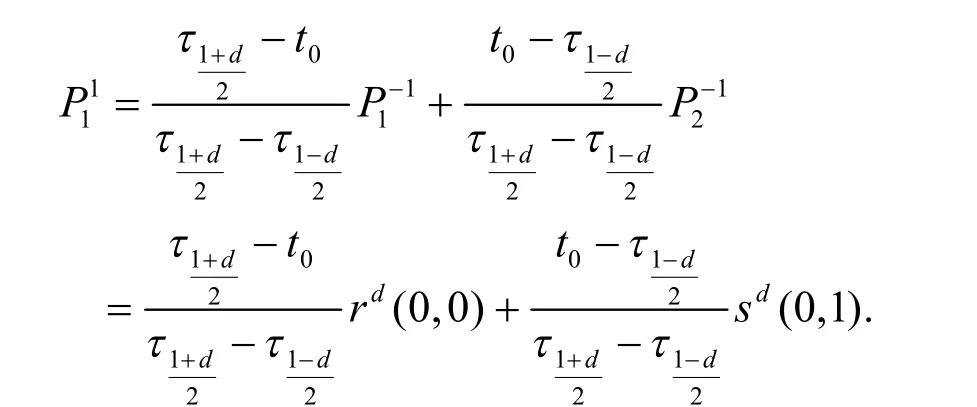
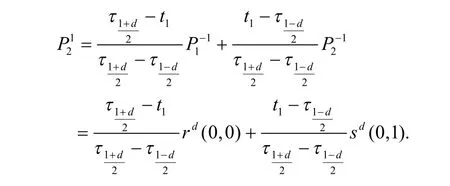

即式(7)成立。
由式(4)得:


即式(8)成立。综上可得:对于任意δ(1 ≤ δ<d,δ是奇数),式(7)、式(8)成立。
在前(d - 1)/2步光滑操作满足引理1的基础上,要证明奇次算法的正确性,我们只需证明最后一层光滑操作满足:
定理1对于奇次d,加细后控制顶点满足:
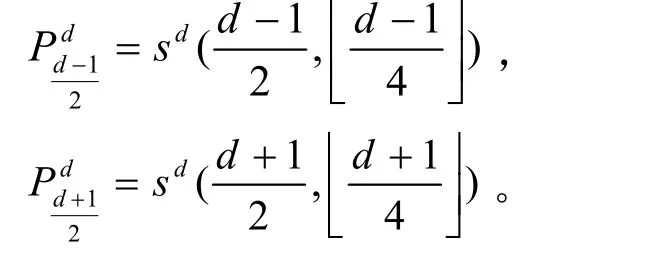
证明:令由式(5)得:

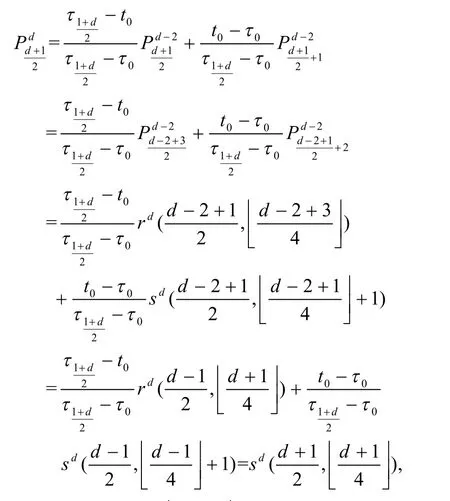
关于偶次算法,也能得到类似的定理,可通过引入两个与函数 rd(m , i )类似形式的开花多项式,证明算法对于偶次情况的正确性。
3 时间复杂度分析
对于次数为 d,初始控制顶点的个数为 n+1的B样条曲线,现对4种任意次的细分算法从加法计算量和乘法计算角度作比较,如表1所示。
由表1可知:任意次均匀B样条细分算法:Lane-Riesenfeld算法,该算法的加法和乘法计算量分别为和。本文算法,Schaefer算法,Cashman算法都是任意次非均匀B样条的细分算法,这些算法的细分过程不同,但是其极限曲线相同。当初始控制顶点个数较多时,可忽略次数对计算量的影响,此时本文算法的加法和乘法计算量约为Lane-Riesenfeld算法的加法和乘法计算量的一半,本文算法与Schaefer算法,Cashman算法的计算量相当。

表1 不同算法所需加法和乘法的计算次数
4 结 论
基于开花方法,提出一种任意次非均匀B样条的细分算法,该算法第一步为加细,双写控制顶点,第二步为层的光滑。通过引入两个开花多项式,证明了算法的正确性。该算法计算量与已有的任意次非均匀 B样条细分算法计算量相当。
重节点会带来细分后节点重数的增加,当节点重数超过B样条曲线的次数时,需要把极限曲线在重节点处一分为二,由此又会产生相应的边界问题,这些都是我们需要进一步讨论的问题。
[1] Chaikin G. An algorithm for high speed curve generation [J]. Computer Graphics and Image Processing, 1974, 3(4): 346-349.
[2] Lane J, Riesenfeld R. A theoretical development for the computer generation and display of piecewise polynomial surfaces [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1980, 2(1): 35-46.
[3] Prautzsch H. Smoothness of subdivision surfaces at extraordinary points [J]. Advances in Computational Mathematics, 1998, 9: 377-390.
[4] Stam J. On subdivision schemes generalizing uniform B-spline surfaces of arbitrary degree [J]. Computer Aided Geometric Design, 2001, 18(5): 383-396.
[5] Warren J. Weimer H. Subdivision methods for geometric design: a constructive approach [M]. Morgan Kaufmann Publishers, 2001.
[6] Zorin D, Schröder P. A unified framework for primal/dual quadrilateral subdivision schemes [J]. Computer Aided Geometric Design, 2001, 18(5): 429-454.
[7] Boehm W. Inserting new knots into B-spline curves [J]. Computer Aided Design, 1980, 12(4): 199-201.
[8] Cohen E, Lyche T, Riesenfeld R. Discrete B-splines and subdivision techniques in computer-aided geometric design and computer graphics [J]. Computer Graphics and Image Processing, 1980, 14(2): 87-111.
[9] Ramshaw L. Blossoms are polar forms [J]. Computer Aided Geometric Design, 1989, 6(4): 323-358.
[10] Vouga E, Goldman R. Two blossoming proofs of the Lane-Riesenfeld algorithm [J]. Computing, 2007, 79(3): 153-162.
[11] Goldman R, Warren J. An extension of Chaikin’s algorithm to B-spline curves with knots in geometric progression [J]. Graphical Models and Processing, 1993, 55(1): 58-62.
[12] Schaefer S, Goldman R. Non-uniform subdivision for B-spline of arbitrary degree [J]. Computer Aided Geometric Design, 2009, 26(1): 75-81.
[13] Cashman T J, Dodgson N A, Sabin M A. A symmetric, non-uniform, refine and smooth subdivision algorithm for general degree B-spline [J]. Computer Aided Geometric Design, 2009, 26(4): 94-104.
A Subdivision Algorithm for Non-uniform B-Splines of Arbitrary Degree
Han Liwen1,2, Yang Yuting3, Qiu Zhiyu1
( 1. College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang Hebei 050024, China; 2. Hebei Key Laboratory of Computational mathematics and Applications, Shijiazhuang Hebei 050024, China; 3. Shacheng Senior Middle School, Zhangjiakou Hebei 075400, China )
A subdivision algorithm is presented for non-uniform B-splines of arbitrary degree in a manner similar to the Lane-Riesenfeld subdivision algorithm for uniform B-splines of arbitrary degree. The algorithm contains two steps: refining and smoothing, and achieves non-uniform B-Splines curve of arbitrary degree. The algorithm is based on blossoming rather than the continuous convolution formula for the uniform B-spline basis functions. Two blossoming polynomials are introduced to verify the correctness of the subdivision algorithm. The subdivision algorithm is more efficient than the classical uniform subdivision algorithm for B-splines of arbitrary degree, and as efficient as those currently available non-uniform subdivision algorithms for B-splines of arbitrary degree.
computer aided geometric design; subdivision; blossoming; B-splines; non-uniform; knot insertion
O 241.5
A
2095-302X (2013)04-0056-06
2012-09-08;定稿日期:2012-11-05
国家自然科学基金资助项目(61170107);河北省教育厅自然科学研究项目(Q2012041)
韩力文(1974-),女,河北石家庄人,副教授,博士,主要研究方向为计算机辅助几何设计,数字几何处理。
E-mail:hanliwen@sina.com
