图解工程静力学研究

林大钧

（华东理工大学机械与动力工程学院，上海 200237）

图解工程静力学研究

林大钧

（华东理工大学机械与动力工程学院，上海 200237）

正投影基本原理可用于求解工程静力学问题，主要介绍图解空间汇交力系和任意力系的基本方法。通过实例说明图解基本原理的应用，以便进行更深入的研究。大多数工程静力学问题可以用代数方法或图解方法予以解决。有些情况下，代数法较易获解，而在许多情况下，图解方法更加快速而经济，用AutoCAD 进行图解将更加有效。

正投影；静力学；CAD软件；图解

图解静力学是一门历史悠远的知识。从阿基米德利用支点思考平衡问题，到达芬奇试图用图示方式思考力学问题，再到荷兰人西蒙斯蒂芬利用绳索研究力学关系。经历数代人的努力，德国人卡尔库尔曼在作为 ETH-Zurich工程学院教授期间于1864年出版了Die Graphische Statik ，为图解静力学奠定了基础，并被世界范围广泛认为是图解静力学之父。然而，由于手工作图精度低，因此图解法已经很少被实际应用，取而代之的是代数法和矢量法，虽然精度得到了解决，但是图解法的直观性、简捷性却丢失了，人的空间思维得不到充分的发挥。近年来，在工程静力学方面美国Hibbeler R C教授著的《工程力学-静力学》（第3版）[1]是美国最受欢迎的工程力学系列教材之一。而美国Ferdina P. Beer撰著的《工程矢量力学（静力学）》（第3版）[2]又有了很大的进展，与《工程力学-静力学》比较，其特点是应用矢量的方法突出了静力学问题求解的直观性，这本教材被我国国外高校优秀教材审定委员会评为优秀教材。沿着这一变革和发展进程，用图解的方法求解工程静力学问题，可发挥画法几何直观性强的优点，并在AutoCAD中进行精度设置可满足工程精度要求。

力、力偶、力矩是静力学的3个基本物理量。因此，首先用正投影方法对这3个物理量进行图示，再结合静力学基本原理建立图解步骤，应用AutoCAD作图功能，实现图示图解。静力学在工程实际中应用很广，实例极多，与代数法、矢量法一样，图解法也须正确的进行受力分析，只是解题形式不同。因此，以上述3个基本物理量的图示图解作为研究的起点，以用图解法解决各种工程静力学问题作为最终目标，在此过程中将会产生许多作图技巧和新的作图方法。本文以空间汇交力系、空间任意力系的实例为载体，对3个基本物理量的图示图解方法及其应用作一个初步探讨。

1 一般位置直线实长、方向角的解析与图解的关系

由于力可以用一带有方向的线段表示，用图解法求解空间力系问题，必然会遇到直线段的实长、投影长、坐标差、方向角的解析与图解的关系。设直线AB对H、V、W三个投影面的倾角分别为α 、 β 、γ，图1(a)所示为直线AB对H面的倾角，其大小可用式(1)表示。

同理，由图1(b)可知，直线AB在V、W投影面上的投影a′b′,a′′b′′与AB实长及其对V、W投影面的夹角三者之间的关系如式(2)所示：

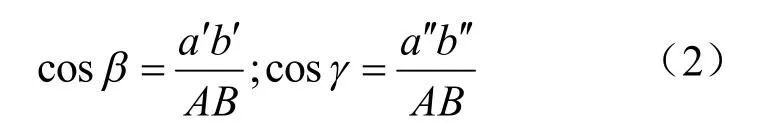
设直线AB上两点的坐标为 A(x1,y1,z1), B(x2,y2,z2)，图1(c)直观地表示了直线AB与投影轴的夹角，其大小如式(3)所示：

联系图1(a)和图1(b)可知α与γz、β与βy、γ与αx互为余角。

图1 直线各参数之间的关系

2 力的图示图解

力是一个抽象的概念，通常力对物体作用效果由其大小、方向和作用点的位置三者确定。因此可用有起点、有方向、有一定长度的线段来表示力。图示就是将力用直线的投影来表示其大小，方向与作用点，如将图1(a)中的AB线段当作一个力，则图1(b)就是该力的图示形式。在力学中力的方向常常是指其方向角即力AB对坐标轴x、y、z的夹角。由图1可知，力对x、y、z轴的方向角与其对W、V、H投影面的夹角互为余角。因此，通过构造直角三角形可求出力对投影面的夹角和与轴的夹角。再以一定比例尺表示单位长度的力，这样就用图示的方法完整地表示了一个力。

根据力学中诸分力可用平行四边形法则求其合力的原理，可以证明将各力的同面投影用平行四边形法则合成后的结果等于合力在该投影面上的投影（证明略）。因此，求诸力的合力也可用平行四边形法则先将诸力的同面投影按此法则合成，然后根据合成后的合力的投影求出合力的大小与方向。

按力学原理：空间汇交力系平衡的必要充分条件是力系的合力等于零。其几何条件就是力的多边形封闭，因此力多边形的投影必封闭且力系中各力的同面投影的合成结果也必等于零。所以求平衡状态空间汇交力系的未知力的问题可转化到投影面上进行图示、图解。而对空间任意力系，则通过将诸力平移的方法，将其转化为汇交力系和力偶系进行图示、图解。力平移是应用空间二直线平行，其同面投影平行的定理得以实现，而因为平移一个力要附加一个力偶才能保持等效应，其力偶矩的大小与力的大小及平移距离有关，因此，会遇到求点到直线的距离的图解问题，这些都是画法几何原理在图解静力学中的应用[3]。

3 图解空间汇交力系[4]

为说明问题方便起见，以具体实例对图解法展开讨论。如图2所示，坦克的质量为8000kg。求解提升坦克时3条绳索中每条绳索的拉力的具体步骤为：

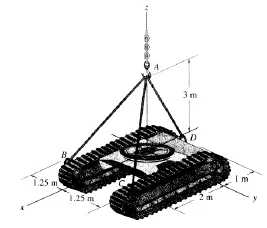
图2 实例1直观图

1） 图示

根据图2直观图中的已知尺寸画出坦克受力投影图，如图3所示。

2） 图解

（1） 在受力投影图上，求出 W× AD与AB× AC 两平面的交线AE。

（2） 利用平行四边形法则，将W向AD、AE分解。因AD为正平线，量得的 a′f′=56.22即为AD绳索的拉力。

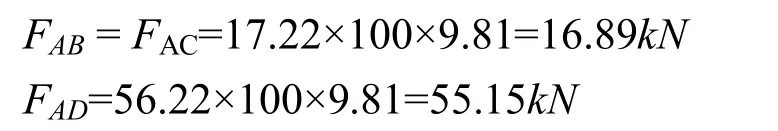
3）使三根绳索受力相等的设计

要使3根绳索受力相等就须重新设计绳索的位置。从图5解题过程可知，绳索拉力大小与绳索与重力矢量的夹角有关，要使3根绳索的拉力相等，可设计3根绳索在一个以重力矢量为轴的圆锥面上，并使它们两两之间的夹角相等，这一要求用图解法很容易实现，如图5中，使3根绳索的水平投影互成120o，其中AD为正平线，其正面投影 a ′d′ =AD，一次投影变换，得到 ΔABC实形所在的投影面，在新投影面上，使，既保证3根绳索长度相等，又处于以重力矢量为轴线的同一圆锥面上，且两两之间夹角相等的位置。显然，此时A点到B、C、D 三点所决定的平面的距离不变，只是B、C、D 三点位置变化了。3根绳索的位置确定后，每根绳索的拉力图解方法与图4相同。最后可得：。（注：图5用的作图比例为1：400）

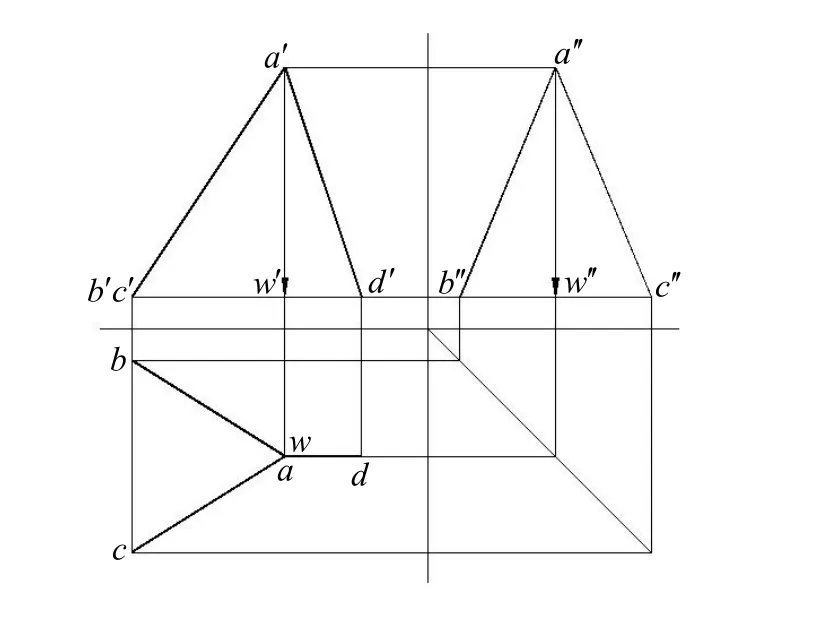
图3 各力投影图

图4 图解法求各力的大小

图5 绳索优化布置

4 图解空间任意力系

通过力的平移可使空间任意力系由汇交力系和力偶系两部分组成。因此，其图解过程包含汇交力系与力偶系2个部分。同样以实例对图解空间任意力系展开讨论。如图6所示，3根绳索缚于支座上。将绳索的力用点A的等效力偶系代替。

图7 支座受力投影图

2） 图 解

汇交力系部分的图解步骤，如图8所示。

（1） 将F1、F2、F3三个力的起始点B、C、D平移到 A点，3个力也随之一起平移，应用AutoCAD的捕捉功能可以精确地实现这一平移。

（2） 用平行四边形法则将 F2、F3合成为F23，再将F23与F1合成为F。

（3）用尺寸标注功能，设定好精度要求，标出 F的大小，根据作图比例可知合力大小为174.16×10=1741.6N。

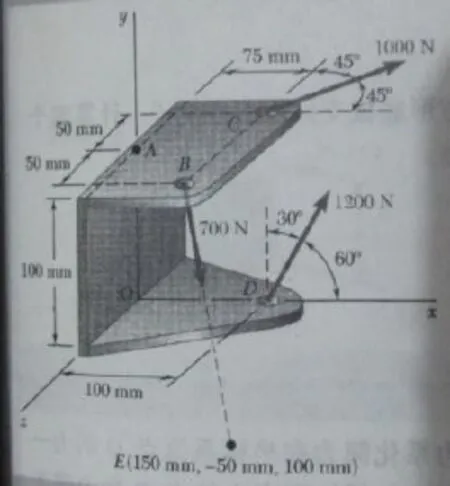
图6 实例2直观图

1） 图 示

如图7所示，根据支座受力的直观图上的尺寸绘制出A、B、C、D 四个点的投影，并以1：10的比例画出过B、C、D三个点的绳索拉力F1、F2、F3的投影。其中F2处于水平位置，其水平投影反映该力的实际大小，F3处于正平位置，其正面投影反映该力的实际大小，而F1处于一般为直，因此用构造直角三角形求实长的方法先求出BE线实长，将F1度量到实长线上，再确定F1的投影。

图8 汇交力系图解

力偶系部分的图解步骤，如图9所示。

（1） 求A点到F1、F2、F3各力作用线的距离。其中，F2的作用线为水平线，在水平投影面上 过a作f2的垂线即可得到A点到F2之间的距离，图中用对齐方式直接标注出 17.68，省略了作垂线。同理，F3的作用线为正平线，在正投影面上过a′作 f3 ′的垂线即可得到 A点到F3之间的距离，图中用对齐方式直接标注出136.6，也省略了作垂线。而F1的作用线是一般位置直线，图中用旋转法将其旋转成正平线，A点也随之旋转，然后在正投影面上标出77.26即为A点到F1作用线的距离。

（2） 求各附加力偶的大小。将各力的大小乘以其平移到 A点的距离即可得到各附加力偶的力矩大小。具体为：

图9 点到力作用线的距离图解

5 结 论

论文中所选用的两个实例具有代表性，用AutoCAD作为工具，作图有精确性，直接将力的大小标注在图上比较直观显见。另外，图解过程也有助于图解训练和实现画法几何的应用价值。为了充分体现图解法的优越性，附录中采用两个实例说明代数法、矢量法的求解过程，以便更加理解基于Auto CAD的图解工程静力学问题是一种值得推广的实用方法。

6 附录[5]

附录1 解析法与矢量法求解过程实例

1） 解析法

由图10可知：

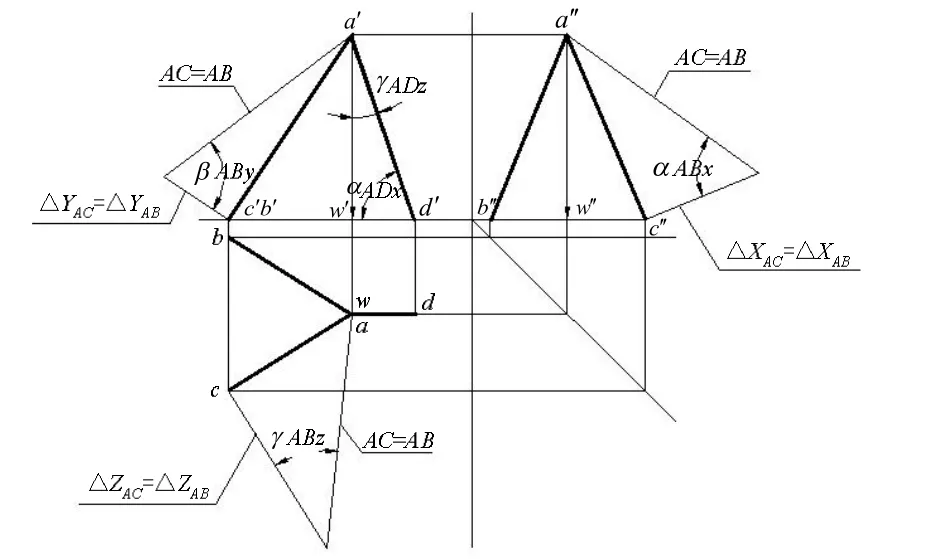
图10 各力对轴的夹角

由图10可求出各力对轴的夹角：

2. 矢量法

以A点为研究对象，受4个力作用，其中有3个力的大小未知。引入i、j、k，将每个力分解为垂直分量：

对于 FAB,FAC，先确定矢量 AB,A C的大小和分量。用 λAB表示沿着AB的单位矢量有：

类似的有：

由于A点平衡，有Σ F =0：

式(8)、式(9)、式(10)、式(11)代入式(12)得：

由式(10)解出：FAB= FAC=16.6kN, FAD=55.2kN

附录2 矢量法求解过程实例

首先，计算从点A到各力作用点的相对位置矢量，并将各力分解为直角坐标分量。显然FB= (700N)λAB，其中采用米和牛顿为单位有

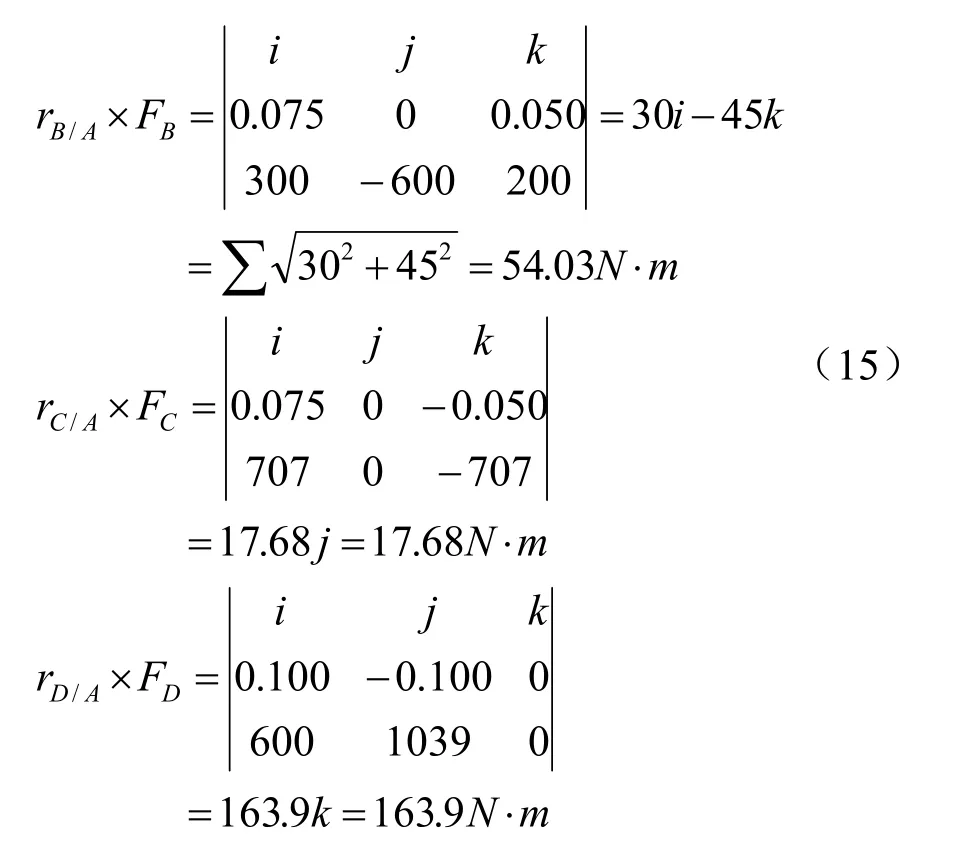
[1] Hibbeler R C. 《工程力学-静力学》(第3版)[M]. 北京: 机械工业出版社, 2003: 89-93.

[2] BEER F P. 工程矢量力学(静力学)(第3版)[M]. 北京: 机械工业出版社, 2003: 124-129.

[3] 张 磊. 徐昌贵, 聂学俊. 图解法的 CAD实现途径[J]. 工程图学学报, 2005, 26(6): 164-167.

[4] 郭新龙, 林大钧, 聂冬金, 等. 基于 AutoCAD的静力学图解方法[J]. 东华大学学报(自然科学版), 2012, 38(5): 601-604.

[5] 哈尔滨工业大学理论力学教研组编. 理论力学(第 6版)[M]. 北京: 高等教育出版社, 2002: 79-88.

Research on Graphical Engineering Statics

Lin Dajun
( School of Mechanical and Power Engineering, East China University Science and Technology, Shanghai 200237, China )

The fundamental principle of orthogonal projection can be used to solve problems that arise in the field of engineering statics. This paper deals mainly with the graphical solution of elementary, concurrent force and forces in space problems. Some actual examples are included to illustrate applications of the simple principles and will encourage further study. Most problems in engineering statics can be solved by either graphical or algebraic methods. In some cases the algebraic solution is more readily obtained. In other cases, the graphical solution is quick and more economical. In a number of cases AutoCAD solutions may be well justified.

orthogonal projection; statics; AutoCAD software; diagram

TP 391.72

A

2095-302X (2013)05-0132-06

2013-01-02；定稿日期：2013-03-28

林大钧（1953-），男，浙江宁波人，教授，主要研究方向为计算机图形学及工程图学。E-mail：Ldj1953@ecust.edu.cn