Delaunay三角网生长算法改进与实现

周 婷， 彭正洪， 密新武

（武汉大学城市设计学院，湖北 武汉 430072）

Delaunay三角网生长算法改进与实现

周 婷， 彭正洪， 密新武

（武汉大学城市设计学院，湖北 武汉 430072）

对一般三角网生长法做了简要介绍和分析，针对限制算法效率提高的关键步骤——“搜索符合条件的第三点”，提出了一种“第三点分区搜索法”的改进算法。通过一系列的圆弧将离散点区域划分成多个分区，构网时规定只可在当前分区和相邻的下一分区搜索第三点，当该分区的离散点搜索完毕后进入下一分区。在Microsoft Visual Studio 2008的环境下使用C++进行编程测试，结果表明，该算法能够加快构网速度，生成的三角形形状良好，具有一定的实际效用。

Delaunay；三角网生长法；分区搜索

DEM，Digital Elevation Model，数字高程模型，主要研究如何将密集分布的采样位置坐标点，通过一定的规则组织在一起，以形成实际的地形空间特征。DEM作为 GIS 数据库中相当重要的空间信息和地形分析模型，它的高效构建算法一直是许多学者研究的焦点。在数字地形建模中，TIN(Triangulated Irregular Network)，不规则三角网，是DEM的一个主要模型，它通过生成一系列互不重叠又相互临接的三角形来逼近实际的地形表面。在所有构建TIN的构网方法中，Delaunay三角网以其相当强的地形拟合综合能力，常常被选取用来生成TIN。

Delaunay三角网是通过满足空外接圆法则和最大最小角法则来保证三角网的唯一性。Delaunay 构网方法一般有3种：分割合并法、逐点插入法和三角网生长法。其中，分割合并法的优点是其实现效率高，缺点是由于算法中大量的递归调用导致算法相当复杂，并且耗用内存很大；逐点插入法的优点是算法实现简单，内存占用少，缺点是时间复杂度差，构网速度慢；而三角网生长法不像分割合并法那样大量的搜索边集、子集，进行并网操作，在算法复杂度上要相对简单一些。但是三角网生长法的关键步骤“搜索满足条件的第三点”，由于其搜索的盲目性导致了大量的时间消耗，特别是随着离散点数据量的增加，其时间复杂度也成倍增加。因此本文首先对三角网生长法的实现算法进行了简要的介绍和分析，在此基础上以缩小第三点搜索范围为原则，对三角网生长法进行了一定程度的优化，最后对算法进行实现，并通过结果分析比较来验证算法优化的效率和可行性。

1 三角网生长法算法与效率分析

三角网生长法的基本算法思路是首先找到所有离散点中相距最短的两点，将其连接作为首三角形的初始边（基边）。然后，按照D-TIN判断法找到包含此边的Delaunay三角形的第三点，连接此点与初始边的两个顶点构成首三角形；再按 D-TIN判断法以首三角形中另外两条边为基线，分别搜索第三点构成另外两条边的Delaunay三角形，依次循环，直至所有离散点均成为D-TIN的端点。

现假定待构网的离散点的个数为n，下面对三角网生长法的基本步骤进行简单介绍与实现效率分析：

第一步：在包含n离散点的点集中寻找任意两个点之间的距离最小的点对，将此两点连接起来作为初始基线。此步骤中需要进行 n*(n-1)/2次的距离计算，并在这n*(n-1)/2个距离结果中找到最小的距离值，因此，此步骤的时间复杂度为O(n2)；

第二步：找首三角形。应用Delaunay判断法在初始基线的右边搜索第三点。D-TIN判断法的具体方法是以基线的两个端点作为向量的起点，依次将其余的未构网的 n-2个点作为向量的终点，利用公式计算两个向量间夹角的余弦值，其中P1和P2分别为基线的两个端点，Pi为还未参与构网的其他点。在这所有的余弦值中，找余弦值最小的点作为首三角形的第三点。此步骤计算n-2个余弦值，并从结果中找到最小余弦值，因此时间复杂度也是O(n)；

第三步：以三角形的三条边为基线，寻找与基线构成三角形的可能的扩展点。一条基线最多是两个三角形的公共边，因此，当基线在寻找可能扩展点的时候，应保证扩展点与基线已构成的三角形的第三点分别位于基线的两侧。否则可能会导致三角形的重叠。以下图（1）的三角形为例，寻找基线T1T2的可能扩展点判断方法如下：

首先给出基线T(1)T(2)的直线方程，记T1(x1, y1), T2(x2, y2)，利用向量的叉乘计算基线的函数方程，直线上任一点(x, y)有：

在这里我们可以对未构网的离散点P(x, y)及上图中T(3)点分别代入直线方程中，并判断f (x, y)的符号，给定以下约定：

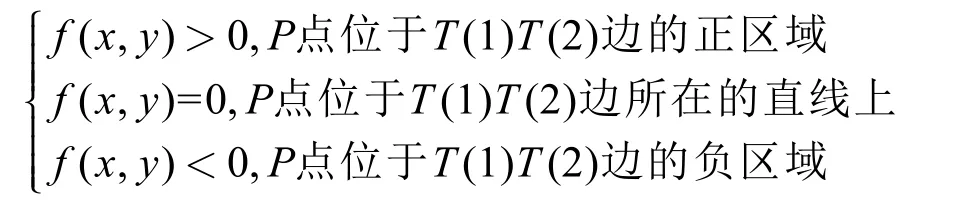
若 f( P)与 f( T (3))同号（即同为正区域或负区域），则 P点不是可能扩展点；若 f( P)与f( T (3))异号，则P点是可能的扩展点。

此步骤主要是对所有未构网的点进行比较判断，其执行的效率也是O(n)，但是，以后每次构建一个三角形都要进行此步，因此，其最终的时间复杂度是O(n2)；

第四步：对于可能的扩展点判断是否满足Delaunay原则。此步骤类似于寻找首三角形的第三点，即在所有可扩展点中寻找余弦值最小的点且构成的边不能为重复扩展边。此过程的时间复杂度为；

第五步：重复第三、第四步直到所有点都连线完毕，则构网结束。

上面分五步介绍了三角网生长法构网的步骤，并在每一步后面给出了时间复杂度的分析。由分析可知，此算法的大部分时间都用在搜索符合Delaunay法则的第三点上了，而由于搜索的盲目性使得很多值的计算是多余的，而且计算所得的中间结果加重了比较筛选的负担，随着数据点的增加，这种弊端更加的明显，构网速度愈发减缓，因此,需要对一般的三角网生长法进行改进，以提高构网速度。

2 三角网生长法的改进算法

改进算法的基本思路是：将所有的离散点进行区域划分，依次对每个区域进行构网，构网方法依旧以三角网生长法为主体，但在进行第三点搜索时约定只在本区域和相邻区域中进行，第三点搜索范围这样设定既防止了大量不必要的计算比较，又减少了子网的并网操作的复杂性。

在改进算法中，如何进行合理的区域划分成为关键所在，直接影响着最终的构网效率。在这里，我们首先找到所有离散点中的X、Y坐标的最大最小值，记作Xmin, Ymin, Xmax, Ymax。

这样点(Xmin, Ymin)和(Xmax, Ymax)可以构建成一个矩形区域，如下图2所示。我们称这一矩形区域为“离散点面积区域”。

图2 离散点区域面积

在离散点面积区域中，以 (Xmin, Ymin)为圆心，以不同的半径画一系列圆弧与矩形边界相交构成闭区域，每一个闭区域我们称为一个分区，在搜索第三点的时候只允许在当前分区和相邻的下一分区进行搜索，其他分区的点暂时被排除在外。在给出具体算法前，我们先阐述几个关键点：

1） 圆心选取为(Xmin, Ymin)；

2） 半径选取。半径的取值相当关键，若半径取值过小会导致在当前分区中无法找到合理的第三点，若半径取值过大或导致算法效率提高不明显，因此，半径不能盲目选取。在这里，离散点区域面积很容易计算得到而离散点的数据点个数已知为n，这样可以得到离散点的平均密度为ρ =S/n。当离散点较为密集的时候，我们可以粗略的认为离散点的相邻两点间平均距离的平方为以 d为基础和标准来选取半径的值就会比较合理。理想情况下，第i个分区的半径为但是，由于d的值是一个粗略估计的距离值，而且实际上任意两点间的距离并不是相等的，因此，直接以为第i个分区的半径并不合理。于是，我们引入相关系数 f，用来将d进行适当放大，得到可取值为2,3,4…根据实际需要f的值是可变的，f的取值也直接影响着分区个数的多少。

3） 分区个数与分区指针。当f的值取定后，分区个数也随即而定。由于离散点面积区域的矩形一致，因此，最后一个分区的半径应该小于等于矩形对角线，于是有因此，分区个数为每一个分区设定一个指针，作为每一个分区的标志。分区搜索法的分区方法如图3所示，M为圆心，1，2，3，4，5分别代表当前分区的指针，构网从A区开始，A区使用三角网生长法构网时只在A区和B区搜索第三点，一旦A区的所有点都参与构网了，则将分区指针移向B区，再对B区进行构网，依此类推，直至所有分区都构网结束。

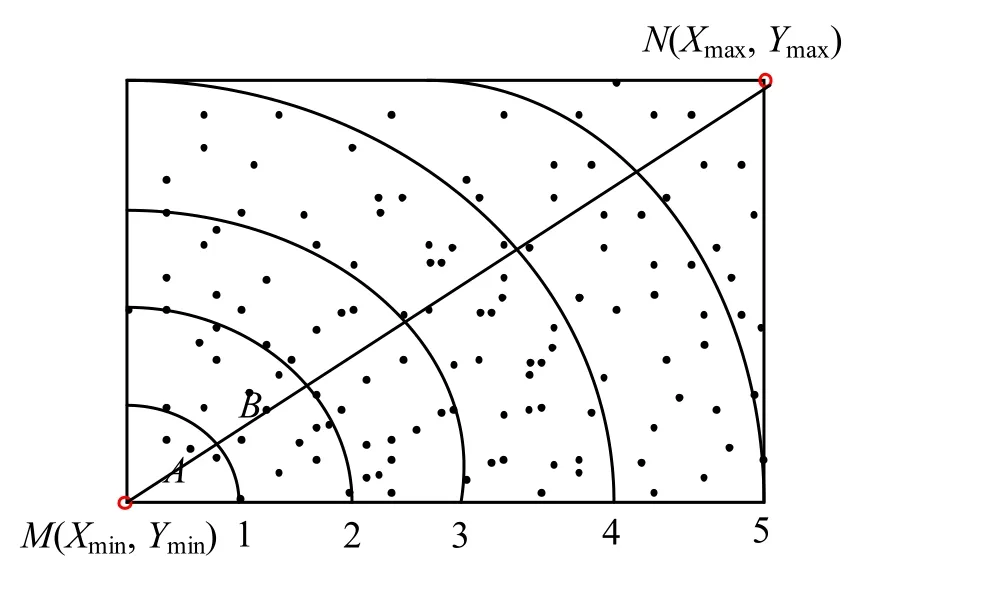
图3 分区搜索法的区域划分

3 改进算法的实现与测试

在本算法中采用容器类(Vector)来存储数据。Vector＜CPoint＞T1 用来存储每一个分区内的离散点，Vector＜CLine＞T2用来存储基线（边），Vector＜CTriangles＞T3用来存储构建成的三角形。在读入点的时候，采用 T1.push_back(point)将点输入容器中，同理通过 T2.push_back(line)将满足条件的边存入容器T2中，将结果三角形存入T3中。

采用“分区搜索法”搜索第三点，以三角网生长法为主体来进行分区构网，基本步骤如下：

第一步：对所有点进行搜索比较，找出所有离散点中的Xmin,Ymin, Xmax,Ymax，建立离散点面积区域；

第二步：以(Xmin,Ymin)为圆心，以f*i*d为半径画圆弧，将离散点面积区域划分为N个区域，并给每个区域赋予指针，唯一标示所指区域。

第三步：计算每一个离散点与圆心的距离，根据距离值与区域半径值得比较可知每一个离散点的所属区域，并将该离散点存储在所属区域的容器中。

第四步：在第k区域，根据Delaunay原则，按照第二节所述的三角网生长算法进行三角网的构建，直到当前区域内的所有点都被扩展完成。

第五步：将区域指针加1，进入下一区域，重复第四步。直到所有的离散点都被扩展。构网结束。

按照以上的算法思路和步骤，笔者在Microsoft Visual Studio 2008的环境下，进行了三角网生长法改进算法的实验，计算结果如图4所示：

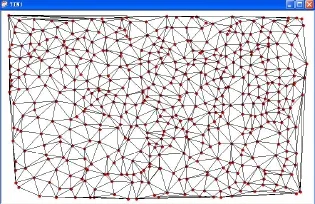
图4 改进算法测试结果图

在相同的计算条件下，将一般的三角网生长法与改进后分区搜索法的耗时比较结果如表1所示。通过实验对比，虽然本算法生成的三角网与一般生长法在某些细节地方存在些许差异，但是三角形形状良好，耗时也有较大幅度的降低，构网速度有明显提高。

表1 改进算法和一般三角网生长法的耗时比较

4 结 束 语

本文首先对三角网生长算法给出了简要的介绍和分析，然后针对算法各步的耗时找到限制算法效率的关键步骤——搜索符合条件的第三点，为提高这一步的执行效率，给出了三角网生长法的改进算法，改进的三角网生长法的关键所在是确定分区半径。最后通过编程实验，将同等条件下的一般三角网生长法的执行时间与改进后的三角网分区搜索生长法的执行时间相比较，测试结果显示改进后的算法在效率上有了很大的提高。

[1] 徐道柱, 刘海砚. Delaunay三角网建立的改进算法[J]. 测绘与空间地理信息, 2007, 30(1): 38-41.

[2] 刘永和, 谢洪波, 袁 策. 一种基于三角网扩张法的 Delaunay三角网逐块归并算法[J]. 测绘科学, 2007, 32(3): 52-54.

[3] 郭兆胜, 张登荣. 一种改进的高效 Delaunay三角网的生成算法[J]. 遥感信息, 2005, (1): 15-17.

[4] 祝志恒, 傅鹤林, 蒲 浩, 等. 构建Delaunay三角网的一种新型生长法——壳外插入法[J]. 铁道科学与工程学报, 2007, 4(6): 67-72.

[5] 侯俊杰. 深入浅出MFC (第2版)[M]. 武汉: 华中科技大学出版社.

[6] Stanley B L, Josée Lajoie 著. C++ primer(第3版)[M].潘爱民, 张丽译. 北京: 中国电力出版社, 2002: 210-227.

[7] 汤国安, 刘学军, 闾国年. 数字高程模型及地学分析的原理与方法[M]. 北京: 科学出版社, 2005: 1.

An Improved Delaunay Triangle Network Growth Algorithm and its Implementation

Zhao Ting, Peng Zhenghong, Mi Xinwu
( School of Urban Design, Wuhan University, Wuhan Hubei 430072, China )

A brief introduction is given for the general Triangle network growth algorithm. An improved algorithm named as “the partition search method of the third point” is provided. First, a series of circular arcs are used to divide the area of discrete points into multiple partitions. Then - the third point is restricted to be searched only in the current partition and the next adjacent partition when building the triangle network. After all the discrete points are added into the triangle network in current partition, the search can be moved into the next partition. Last, the C++ programming language is used to test the algorithm in Microsoft Visual Studio 2008 environment. The result shows that the improved algorithm can improve the speed of building the network, and the generated triangular shape is good.

Delaunay; triangle network growth algorithm; partition search

P 221.1

A

2095-302X (2013)05-0012-04

2013-07-15；定稿日期：2013-07-15

周 婷（1989-），女，湖北天门人，硕士研究生，主要研究方向为计算机应用。E-mail：305302163@qq.com

彭正洪（1967-），男，湖北天门人，教授，博士研究生导师，主要研究方向为计算机图形图像处理，数字化设计与仿真。

E-mail：laopeng129@vip.sina.com

密新武（1953-），男，湖北武汉人，教授，主要研究方向为计算机辅助设计。E-mail：mixinwu@126.com