求解各向异性介质涂覆的薄壳元-边界积分法
2013-03-12胡皓全
雷 霖 胡 俊 胡皓全
(电子科技大学电子工程学院,四川 成都611731)
引 言
在武器系统的研制中,隐身设计是一项非常重要的军事需求[1-6].除外形设计技术之外,目标表面涂覆吸收材料也是隐身设计中经常使用的一项技术,针对涂覆吸收材料目标的电磁散射特性建模方法也就显得很重要.传统解析方法可以处理各向异性媒质涂敷导体球的电磁散射,但不能用于任意涂敷复杂导体情形,使得解析方法有很大的局限性[5].有限元方法是一种非常有效的方法,它在处理复杂非均匀介质目标的电磁散射与辐射问题中有着极大的优势[7].单纯的有限元方法需要应用吸收边界条件去截断计算区域的边界.有限元方法与边界元混合方法综合了两种方法的优势,只需将截断边界选取在目标的边界上,使得内存的需求和计算时间大为降低[8-11].但是,由于涂覆材料的厚度很薄,无论采用积分方程方法还是采用有限元方法与边界元混合,均会遇到待求未知量多、矩阵病态的困难.为实现薄层介质的高效数值求解,阻抗边界条件技术被广泛使用[12],薄介质片及多层薄介质片模型也被提出应用在积分方程法用以进一步降低未知量的数目[13-15].为提升有限元方法分析薄层介质的效率,D.Wulf,R.Bunger发展了三棱柱单元[16].Z.Ren进一步发展了薄壳单元[17],该单元是三棱柱单元的退化,它类似于三角形面单元,对于薄层介质只需要进行面剖分,而不需要进行体剖分.采用薄壳单元可以极大地降低未知量和计算时间.该方法也被应用到时域有限元方法中[18].
由于涂覆目标往往是金属的,在本文中主要处理涂覆各向异性介质的导体目标的电磁散射问题.首先,阐述有限元-边界元方法处理各向异性媒质的基本原理,介绍了薄壳单元的性质及与有限元-边界元方法的结合.通过对比验证了使用薄壳单元分析各向异性介质涂敷金属球和各向异性介质涂敷金属立方体电磁散射的精确性及优势,并给出了使用薄壳单元分析不同涂敷厚度对各向异性涂敷金属立方体电磁散射特性的影响和不同各向异性介质涂敷时对金属立方体电磁散射的影响,得出了有益的结论.
1 有限元-边界积分方法基本原理
研究导体目标涂覆各向异性介质材料的电磁散射问题.在各向异性媒质中的电场满足麦克斯韦方程为
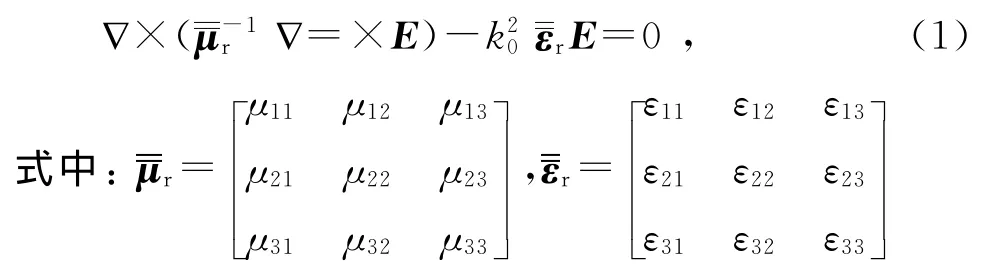
分别是媒质的相对磁导率和介电常数;k0是自由空间的波数.
在各向异性媒质与自由空间的边界上,电场满足下列边界条件:
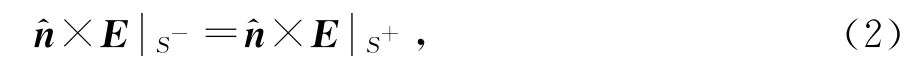
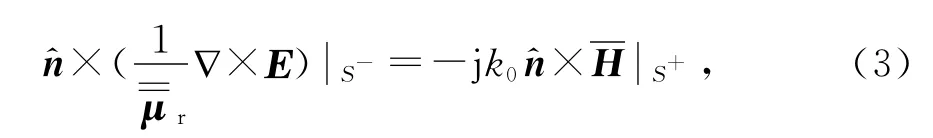
对于各向异性媒质区域,用有限元方法建立方程为
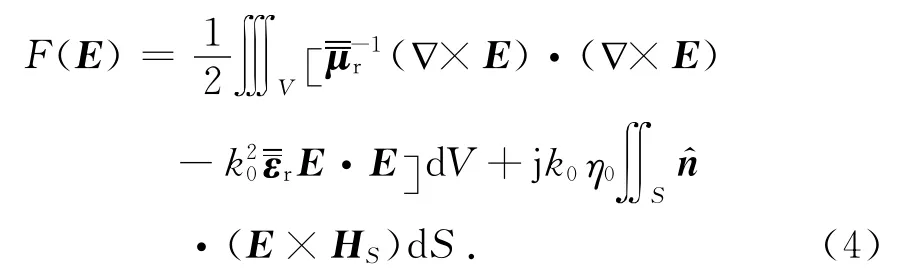
对上述方程离散并应用权函数,可得到下面的矩阵方程为
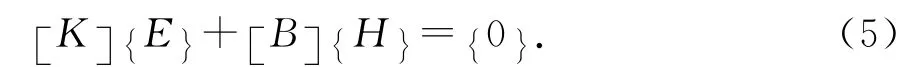
由于这个方程有两个未知量,要求解还需要建立另一个方程.对于边界上的场量,用积分方程方法建立另一个方程,联立两个方程即可求解.
积分方程分为电场积分方程和磁场积分方程:

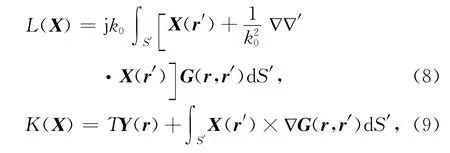
通常为了避免内部谐振,需要将两种方程混合在一起构成混合场积分方程.将混合场方程进行离散并应用权函数,可得到下面的矩阵方程为
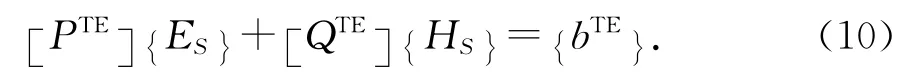
内外两个区域的场通过边界条件联系起来,即联立式(5)和式(10),可将整个问题用下面的矩阵方程表示为
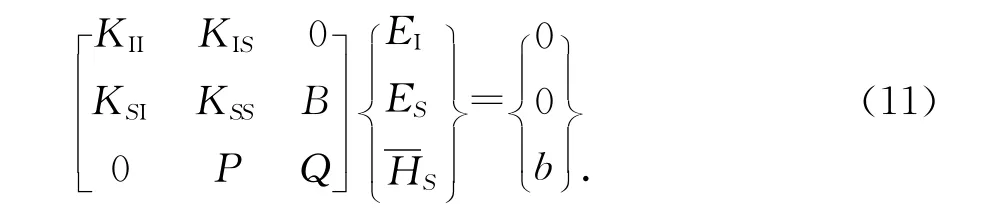
求解方程(11)就可以得到边界上及媒质内部的场量,从而可以进行进一步地分析其散射特性.
2 薄壳单元及与有限元-边界积分方法的结合
如图1所示,在薄壳单元中,将沿高度方向的矢量场表示为三个结点上的法向场,在薄壳单元中就由沿上下表面的棱边场和结点上的法向场构成所有的场量.高度d方向的场的变化可以用一个线性函数β(z)来表示,并且有∇β=-n^/d.上下表面的棱边场的基函数分别用βNj(j=1,2,3)和β′N′j(j=1,2,3)来表示(Nj和N′j是三角形单元的棱边基函数).结点处场的基函数用Lj,j=1,2,3来表示(Lj是体积坐标).
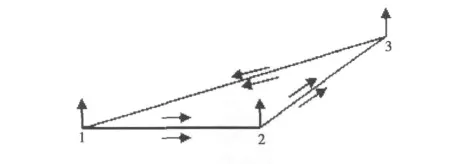
图1 薄壳单元的结构及矢量方向
在薄壳单元中的电场可以表示为[7]:

采用薄壳单元,在薄层介质中的体积分就可以转换为面积分.有限元方程可写为
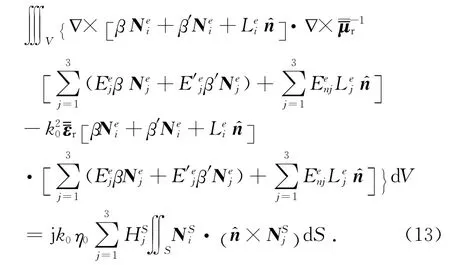
式(13)中,体积分的处理类似于下面几个式子:
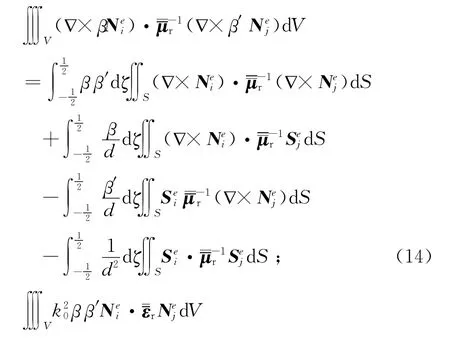
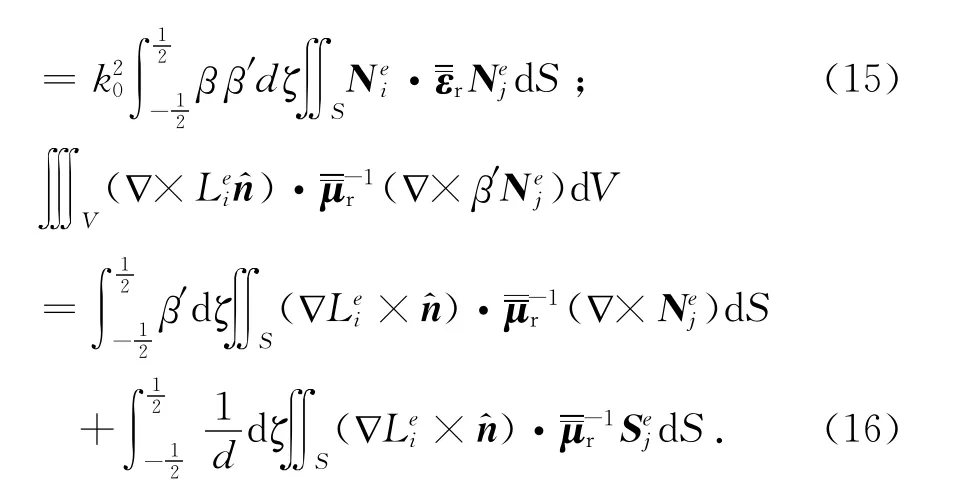
对于导体涂敷各向异性介质的情况,矩阵方程可改写成
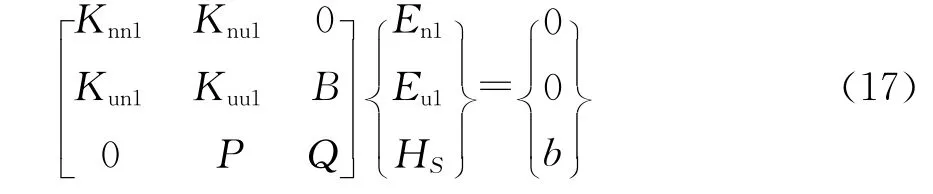
式中:En1是结点处法向电场展开系数;Eu1是上表面棱边电场展开系数.
3 数值结果
为了验证采用薄壳元的有限元-边界积分方程方法的精确性,进行了下列考察.
3.1 介质涂敷导体球
介质涂敷导体球参数的结构参数均为:k0a=1,厚度为a/30.不同的只是介电常数.
1)各向同性介质涂敷导体球
为验证程序的有效性,先用采用薄壳单元的有限元-边界积分方法的针对各向异性介质涂敷导体雷达散射截面(Radar Cross-Section,RCS)的程序计算各向同性介质涂敷金属球的双站RCS,选择相对介电常数为=4.其结果如图2所示,可见其计算结果与解析解结果完全吻合,证明该方法的精度是可靠的.
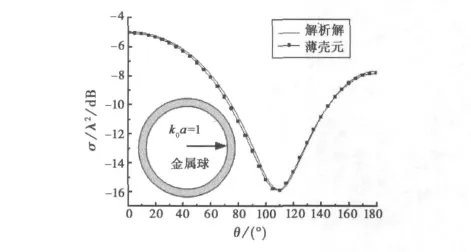
图2 各向同性介质涂敷金属球双站RCS
2)各向异性介质涂敷导体球
将各向同性介质换成各向异性介质,通过改变介电常数来对比传统有限元-边界积分方程方法与使用薄壳元的有限元-边界积分方程方法的计算结果,以证明其精确性和优越性.
两种方法的结点数、单元数、内存和未知量的对比如表1所示,从表1可知采用四面体单元计算所需计算机内存、单元数、未知量分别是采用薄壳元的1.7倍、2.44倍、1.3倍.

表1 两种方法对比
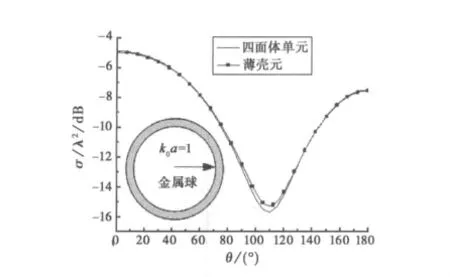
图3 各向异性介质涂敷金属球双站RCS
3.2 介质涂敷金属立方体
计算介质涂敷金属立方体的结构均为:边长0.1 m;波长0.1m;入射波仅有分量,入射波方向θinc=45°,φinc=0°.不同的是介质厚度和介电常数.
1)各向同性介质涂敷金属立方体
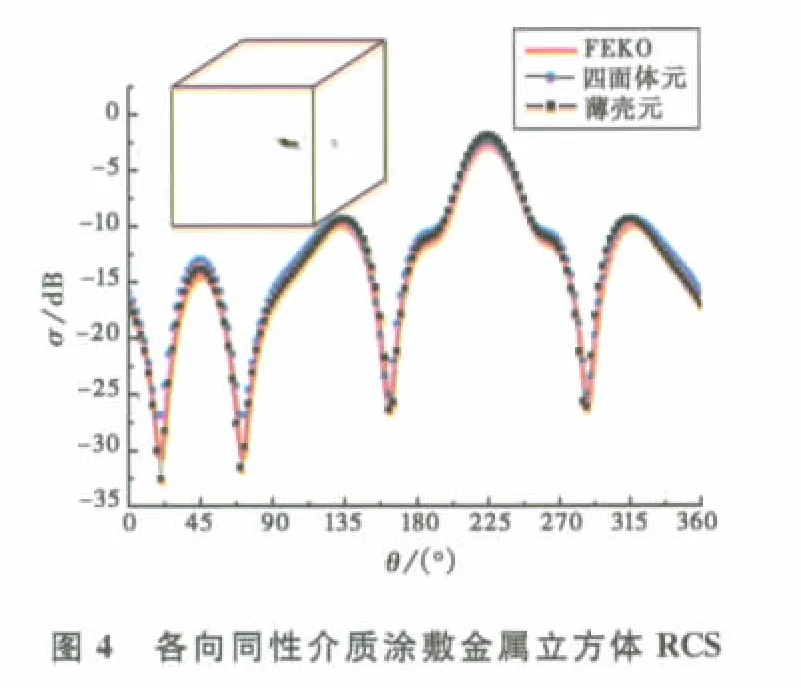
为验证方法的精确性,先用采用薄壳单元的有限元-边界积分方法计算各向异性介质散射特性的程序计算各向同性介质=4,介质厚度为0.001m时的双站RCS.从图4可以看出:采用薄壳元的有限元边界积分方程方法与FEKO软件的计算结果非常吻合,与传统有限元-边界积分方程方法也比较吻合.
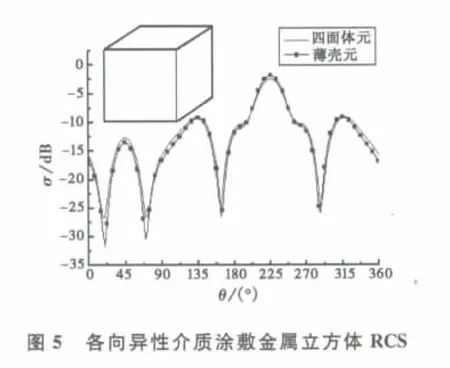
2)各向异性介质涂敷金属立方体
两种方法的结点数、单元数、内存和未知量的对比如表2所示,从表2可知采用四面体单元计算所需计算机内存、单元数、未知量分别是采用薄壳元的1.92倍、2.7倍、1.4倍.

表2 两种方法对比
3.3 参数改变对RCS的影响
通过改变各向异性介质涂层的厚度和参数来看对双站RCS有什么影响.
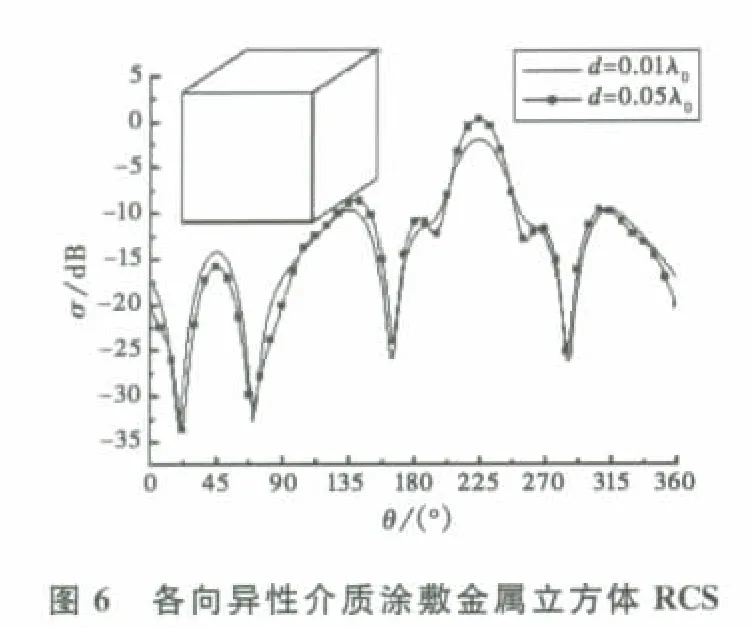
1)厚度对RCS的影响
选择涂层的介电常数
2)不同介质参数对RCS的影响
采用薄壳元的有限元-边界积分方法分析改变介质参数对RCS的影响,选择下面几种不同的参数=εr1、=εr2、=εr3进行比较,结果如图7所示,其中0表示的是没有涂敷的金属立方体.

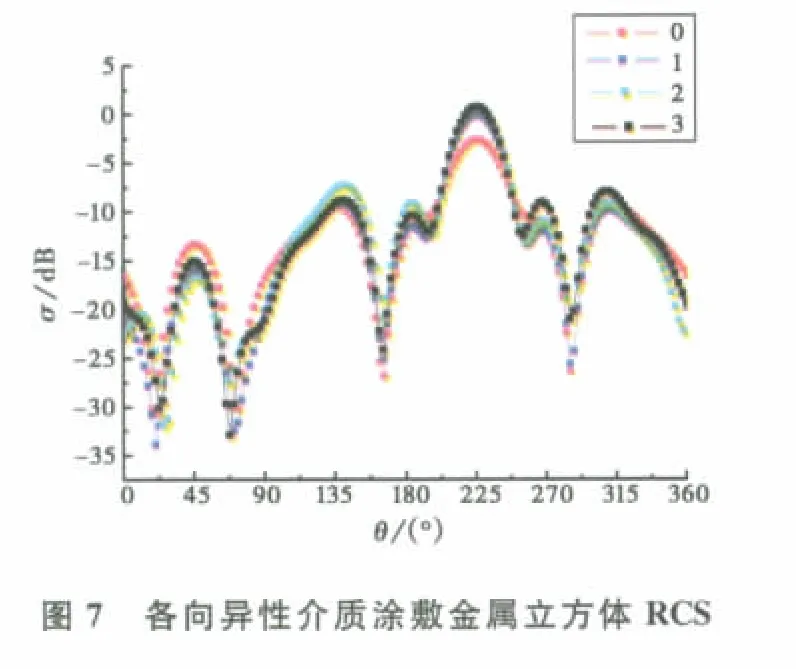
从图7可以看出,没有涂敷各向异性介质的金属立方体比1号介质的前向RCS减少了约5dB,后向RCS增大了约5dB.从前三种介质的计算结果对比发现,1号介质与3号介质由于材料类似,对角线元素的值变化不大所以结果相差不大,2号介质与1,3号介质由于材料不同,所以对结果有一定影响,在本文所选介质的情况下,前向RCS变化不大,但2号介质的后向RCS比1、3号介质减小了约2dB.
4 结 论
通过使用四面体单元的有限元-边界积分方程方法与使用薄壳单元的有限元-边界积分方程方法的对比可以看出:采用薄壳元的有限元-边界积分方法与采用四面体的有限元-边界积分方法相比具有比较高的精度,无论是所需剖分单元数量、未知量还是所需计算机内存上,前者都明显优于后者,采用薄壳元的有限元-边界积分方法在计算各向异性介质涂敷导体时能节省大量的计算机内存和计算时间,剖分越密,效果越明显.由于实际工程中使用吸波材料的厚度都在0.1λ0以下,前面的数据也证明该方法计算厚度为0.1λ0各向异性介质涂敷导体目标双站RCS的精度还是符合要求的,从而证明了该方法分析各向异性介质涂敷导体电磁散射的可行性.
从采用薄壳单元来分析当涂敷各向异性介质的厚度改变对目标双站RCS的影响中可以看出:介质厚度的改变对目标RCS有很大的影响.
从采用薄壳单元来分析当涂敷各向异性介质的介电常数改变对目标双站RCS的影响中可以看出:涂敷各向异性介质材料与不涂敷介质材料对导体目标的电磁特性有很大影响,并且由于介电常数的不同,其散射特性也有所不同.
[1]余定峰,何思远,朱国强,等.各向异性材料涂敷目标电磁散射特性仿真[J].电子与信息学报,2011,33(7):1718-1721.YU Dingfeng,HE Siyuan,ZHU Guoqiang,et al.Simulation of the electromagnetic scattering for target coated with anisotropic materials[J].Journal of Electronics & Information Technology,2011,33(7):1718-1721.(in Chinese)
[2]阙肖峰,聂在平,胡 俊.导体介质组合体电磁分析的建模与计算[J].电报科学学报,2008,23(3):396-401.QUE Xiaofeng,NIE Zaiping,HU Jun.Electromagnetic modeling and calculation for composite conducting and dielectric objects[J].Chinese Journal of Radio Science,2008,23(3):396-401.(in Chinese)
[3]樊振宏,朱 剑,曹海平,等.复杂媒质电磁散射特性的有限元-边界元方法分析[J].电报科学学报,2009,24(3):452-456.FAN Zhenhong,ZHU Jian,CAO Haiping,et al.Computation of scattering from the complex media targets with the hybrid finite-element boundary integral method[J].Chinese Journal of Radio Science,2009,24(3):452-456.(in Chinese)
[4]陈博韬,谢拥军,李晓峰,等.各向异性材料部分涂敷导体的散射特性研究[J].电波科学学报,2009,24(6):992-996.CHEN Botao,XIE Yongjun,LI Xiaofeng,et al.Scattering characteristic of conducting targets with partially-coated anisotropic medium[J].Chinese Journal of Radio Science,2009,24(6):992-996.(in Chinese)
[5]耿友林,吴信宝,官伯然.导体球涂敷各向异性铁氧体介质电磁散射的解析解[J].电子与信息学报,2006,28(9):1740-1743.GENG Youlin,WU Xinbao,GUAN Boran.The analytical solution to the electromagnetic scattering by an anisotropic ferrite-coated conducting sphere[J].Journal of Electronics &Information Technology,2006,28(9):1740-1743.(in Chinese)
[6]王 湃,周乐柱,谭云华,等.不同吸收涂层对三维复杂目标的RCS影响的分析[J].微波学报,2005,21(2):33-37.WANG Pai,ZHOU Lezhu,TAN Yunhua,et al.A-nalysis of impacts of various RAM on RCS of 3-D complex targets[J].Journal of Microwares,2005,21(2):33-37.(in Chinese)
[7]金建铭.电磁场有限元方法[M].西安:西安电子科技大学出版社,1998.
[8]JIN Jianmin,VOLAKIS J L.A hybrid finite element method for scattering and radiation by microstrip patch antenna and arrays residing in a cavity[J].IEEE Transactions on Antennas and Propagation,1991,39(11):1598-1604.
[9]JIN Jianmin,VOLAKIS J L.A finite element-boundary integral formulation for scattering by three-dimensional cavity-backed apertures[J].IEEE Transactions on Antennas and Propagation,1991,39(1):97-104.
[10]SHENG Xinqing,JIN Jianmin,SONG Jiming,et al.On the formulation of hybrid finite-element and boundary-integral methods for 3-D scattering[J].IEEE Transactions on Antennas and Propagation,1998,46(3):303-311.
[11]JI Yun,ALI M W,HUBING T H.EMC applications of the EMAP5hybrid FEM/MOM code[C]//IEEE International Symposium on Electromagnetic Compatibility.Denver,August 24-28,1998:543-546.
[12]HARRINGTON R F,MAUTZ J R.An impedance sheet approximation for thin dielectric shells[J].IEEE Transactions on Antennas and Propagation,1975,23(4):531-534.
[13]LU Caicheng.A modified thin dielectric approximation for calculation of EM scattering by dielectric objects with thin material coating[C]//IEEE Antennas and Propagation Society International Symposium.Honolulu,June 9-15,2007:2809-2812.
[14]CHIANG I T,CHEW W C.Thin dielectric sheet simulation by surface integral equation using modified RWG and pulse bases[J].IEEE Transactions on Antennas and Propagation,2006,54(7):1927-1934.
[15]HE Shiquan,NIE Zaiping,YAN Su,et al.Multilayer TDS approximation used to numerical solution for dielectric objects[C]// Asia-Pacific Microwave Conference.Macau,December 16-20,2008:1-4.
[16]WULF D,BUNGER R.A new hybrid finite element method for thin material structures[C]//IEEE Antenna and Propagation Society Symposium.San Diego,July 5-11,2008:1-4.
[17]REN Z.Degenerated prism elements-general nodal and edge shell elements for field computation in thin structures[J].IEEE Transaction on Magnetics,1998,34(5):2547-2550.
[18]ERIK A,FREDRIK E.Thin sheet modeling using shell elements in the finite-element time-domain method[J].IEEE Transactions on Antennas and Propagation,2006,54(1):28-34.
