基于发射信号预处理的包络移动补偿方法
2013-03-12刘红明何子述
骆 成 李 军 刘红明,2 何子述
(1.电子科技大学电子工程学院,四川 成都610054;2.空军试验训练基地,甘肃 兰州732750)
引 言
雷达高速目标的回波往往存在跨距离单元和跨多普勒单元走动,给相参积累带来损失,积累前需进行补偿.针对该问题的研究已有一定的成果,如文献[1]提出的包络插值移位法,该方法计算量小,且补偿效果较好,但文献[2]中指出包络插值移位法会引入额外的幅度调制,产生寄生旁瓣,将严重干扰对目标的检测与跟踪性能.Keystone变换[3-5]补偿效果比较理想,且不需要目标速度信息,但计算量很大.分数阶傅里叶变换[6-7]属于一种广义的傅里叶变换,其计算速度较快,但是对于先验信息未知的目标需要对目标速度进行搜索,运算量大.另一些常见的方法有:非线形最小二乘法[8],距离门拉伸[9],滑窗与检测前跟踪相结合的方法[10].这些方法都有一定的补偿效果,但大多只能完成对距离走动或多普勒走动中一个方面的补偿,且处理较为复杂.
本文把研究方向集中到发射信号上,结合现在广泛应用于信号源的直接数字频率合成(Direct Digital Synthesizer,DDS)技术,对发射信号进行预处理,并由此提出一种基于发射信号预处理的回波包络移动补偿方法:在发射端调整基带信号的脉宽以得到实际的发射信号;在接收端对回波进行传统的雷达信号处理,即可获得包络对齐的回波信号,该算法简易有效,处理时无信噪比(Signal To Noise Ratio,SNR)损失;结合解线性调频法,完成了对距离走动和多普勒走动两个方面的同时补偿.仿真结果证明所提方法的包络补偿效果较好,能大大提升积累增益,有效改善目标的检测性能.
由于当前各类飞行器的速度越来越快,针对高速目标的检测与跟踪问题也成为了研究热点和难点,本文所提的方法能够在一定补偿速度误差范围内有效地补偿目标的跨距离单元和跨多普勒单元走动,因而具有很好的应用前景.
1 回波特性分析
如图1所示,假设t时刻,目标处于点P,以速度vr水平沿Y轴正向高速运动,雷达位于Q处.PQ为雷达与目标的t时刻位置连线,目标速度方向与PQ的夹角为θ,t时刻的距离为R0.经过时间t1,发射信号刚好照射到目标身上,此时目标运动到点P′,二者间的距离变为R(t1).
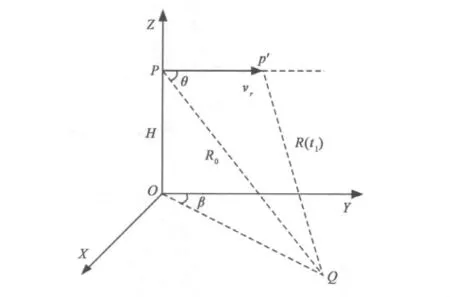
图1 雷达与目标的几何位置关系图
设发射信号的第n个脉冲具有如下的形式
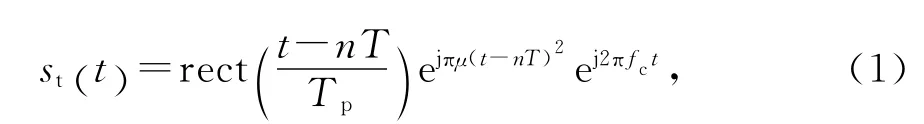
式中:rect(·)为矩形函数;T为雷达周期;Tp为脉冲宽度;μ为调频斜率;fc为载频.根据上述模型,回波脉冲为

式中:τ(t)=pt2+kt0+(1-k)t为传输延时;t0=2R0/(c+v)为回波前沿;压缩系数k=(c+v)/(c-v);v为雷达与目标的相对速度;常数p≈a/c;a为相对加速度;c为光速.
由于目标速度很大,加速度对回波包络走动的影响占总体走动的比例很小,通常在10-4量级,故可以忽略不计.则回波的快时间维包络前沿可近似为

从式(3)可以看出,回波包络将随脉冲个数n的变化而出现包络移动现象.直接对回波进行积累将有能量损失,需要先进行包络移动补偿.
由式(2)的指数项知,回波存在时间的二次相位项,直接积累会导致能量损失.需要先校正回波的多普勒走动,然后再积累.
2 基于发射信号预补偿的包络移动补偿
为了解决上述问题,现有方法都是对回波进行处理,但回波中的杂波和噪声等无疑加大了处理的难度.本小节针对发射信号,提出一种新的包络移动补偿方法:通过对原始发射波形的优化设计,在发射端结合DDS技术对脉冲进行预补偿,将处理后的脉冲作为实际的发射信号,接收端收到的回波,其包络在快慢时间域内可自动对齐,即完成了距离走动的校正;为了增加算法的通用性,考虑加速度对积累的影响,结合解线性调频法补偿多普勒走动,实现了对距离走动和多普勒走动的同时补偿;最后,用补偿后的信号与原始发射信号匹配,并通过傅里叶变换(Fast Fourier Transform,FFT)进行相参积累.
预补偿结合解线性调频法同时补偿距离和多普勒走动的总体处理框图如图2所示.
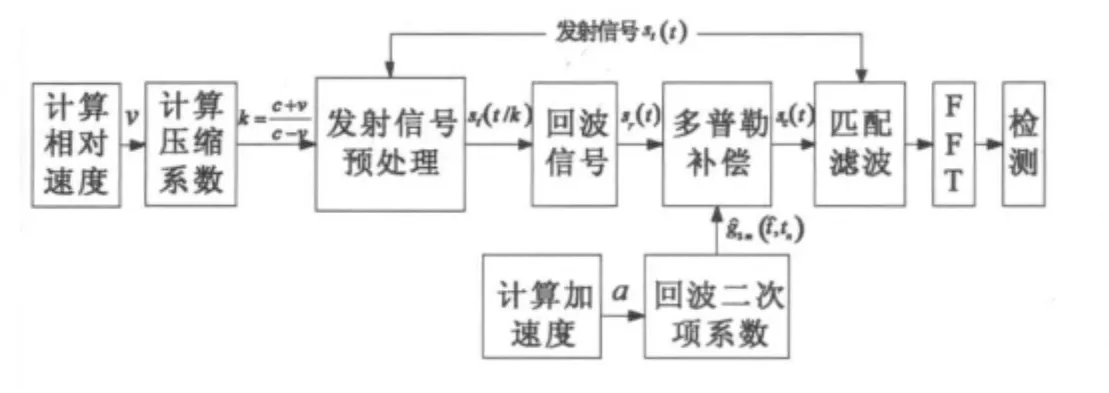
图2 总体处理框图
对式(1)的信号进行预补偿,得到新的发射信号为

与其对应的回波信号为

式中k0跟回波压缩系数k一样,也是由目标的速度决定的,理想情况下,有k0=k.实际应用中虽然往往难以预知目标的确切速度,但雷达在跟踪阶段,对目标的运动参数具有一定的先验信息,由于系统具有一定的多普勒容限[11-12],即使预补偿速度与目标速度不同而导致k0≠k,其误差Δk=也会非常小,对补偿效果的影响可以忽略不计,故可认为k0=k一直近似成立.此时式(5)可写为

对比式(6)和式(1)可知,通过对发射信号进行预补偿,得到的回波脉冲宽度与发射信号的脉宽相同.回波信号在快时间维的包络前沿=t-nT=t0是一个常数,即说明通过对发射信号进行预补偿,实现了对回波信号的包络走动校正.
完成了对距离走动的补偿,若目标做匀速运动或加速度影响很小,可直接进行相参积累;若目标存在较大的加速度,还需先补偿多普勒走动,再进行相参积累.根据解线性调频法的思路[13],对多普勒走动进行补偿,可得
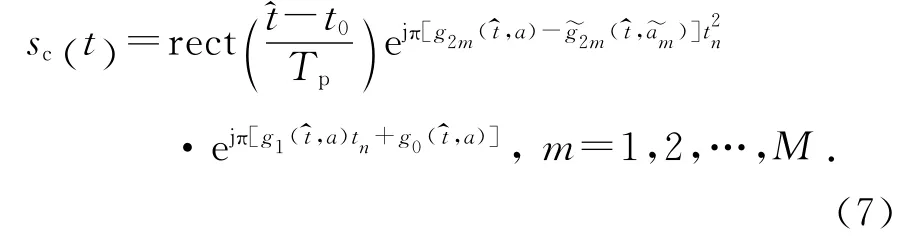
式中:g2m,am)为gm,a)的估计值;am为a的估计值.当am与a很接近甚至a~m=a时,式(7)回波的多普勒走动将得到很好的补偿.
经过解线性调频法处理后的回波,完成了对距离走动和多普勒走动的同时补偿,可以表示为
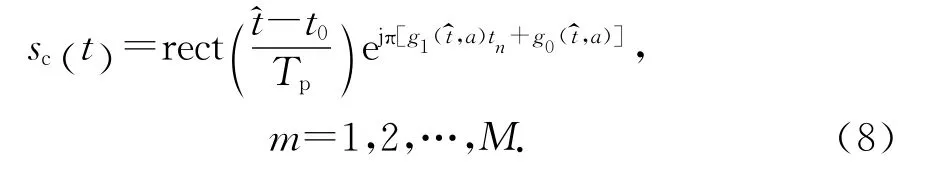
3 仿 真
为验证上述算法的补偿效果和检测性能,在理想补偿的情况下,即k0=k时,分别给出未补偿时的包络走动现象、补偿前后的积累效果对比和补偿前后的检测性能对比;为了说明预补偿的可行性和有效性,给出k0≠k时的补偿积累效果对比.
在如下仿真条件下进行理想补偿的仿真:目标速度4km/s,夹角θ=7°,等效径向加速度约19.5 m/s2,初始距离 100km,雷达周期 1ms,脉宽0.1ms,脉冲数256个,采样率1MHz.
图3给出了在不进行任何补偿的情况下,回波经过匹配后,第一个峰值与最后一个峰值的位置对比,可以从中清楚地看到包络的走动现象.
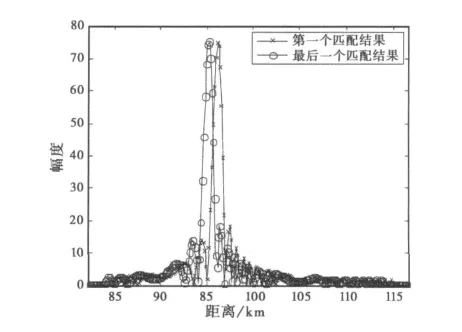
图3 不进行任何补偿时的包络走动现象
图4给出了在完全不补偿、只补偿距离走动和两方面都补偿三种情况下的相参积累输出对比,图中用完全不补偿的最大结果对三条曲线进行了归一化.可以看出,完全不补偿时,匹配输出严重展宽,积累效果很差;而在完成了距离补偿后,积累效果明显改善,增加了约2.36倍;补偿了多普勒走动的影响后,积累效果还有一定的提升,达到约2.65倍,这是加速度较大时的情况,如果加速度变小,多普勒走动对积累的影响将随之减小.
图5对比了补偿前后的检测性能,与完全不补偿相比,补偿后可以有效改善相参积累的效果.


当k0≠k时,考虑仿真条件为:雷达周期T=1 ms,脉宽TP=0.1ms,使用线性调频(Linear Frequency Modulation,LFM)信号(该信号本身就具有较好的多普勒容忍性),信号带宽B=0.5MHz,积累脉冲个数200个.为了涵盖大部分的目标,选择的可能雷达目标相对速度的范围为0~6km/s,并把预补偿速度设置为v=3km/s.考虑到速度误差的对称性,仿真时只取了比补偿速度更大的相对速度(比补偿速度更小的相对速度的补偿效果可由对称性得出),从3km/s起以1km/s为步长选择了4个不同的可能相对速度进行仿真.仿真结果如图6所示.

图6 不同相对速度的匹配滤波结果
图6的仿真结果表明,当可能的相对速度范围为1~5km/s时,用3km/s对其进行预补偿,虽然在两个速度不相同的情况下会有一定的补偿损失,但仍然可以获得较好的补偿效果,说明速度的误差在多普勒容限之内;而当相对速度与补偿速度之差达到3km/s时,损失接近最大值的0.707倍,即3 dB,此时的补偿效果恶化较为严重,说明此时的速度误差已超出了多普勒容限范围.由此可以得出结论,在一定的速度误差范围内,本文所提方法可以有效地补偿目标包络移动.
4 结 论
本文将回波信号转化到快慢时间域,详细分析了动目标回波特性,并结合DDS技术,充分发挥其采样灵活的特点,提出了一种可用于雷达跟踪阶段的预补偿算法,并结合解线性调频法,同时分析并补偿了目标跨距离单元走动和跨多普勒单元走动的问题.从理论分析和仿真结果可以看出,所提算法通过对发射信号进行预处理,可以有效地在一定速度误差范围内补偿目标的跨距离单元走动,并通过解线性调频法补偿了目标的跨多普勒单元走动,从而实现了回波脉冲间的相参性,大大提高了长时间积累的增益,改善了雷达的检测性能.同时,本算法结合了当前研究的热点和难点,计算量小,易于实现,在工程实际中具有很好的应用前景.
[1]朱永峰,李为民,陈远征,等.Chirp雷达对高速运动目标有效相参积累的算法研究[J].系统工程与电子技术,2004,26(10):1397-1399.ZHU Yongfeng,LI Weimin,CHEN Yuanzheng,et al.Effective coherent integration algorithm for highspeed moving targets in chirp radar[J].Systems Engineering and Electronics,2004,26(10):1397-1399.(in Chinese)
[2]刘红明,何子述,杨新亮,等.一种有效降低寄生频谱的包络移动补偿方法[J].信号处理,2010,26(4):573-576.LIU Hongming,HE Zishu,YANG Xinliang,et al.A valid motion compensation for reducing parasitical spectrum in long time coherent integration[J].Signal Processing,2010,26(4):573-576.(in Chinese)
[3]SU Junhai,XING Mengdao,WANG Genyuan,et al.High-speed multi-target detection with narrowband radar[J].IET Radar Sonar Navig,2010,4(4):595-603.
[4]PERRY R P,DIPIETRO R C,FANTE R L.SAR imaging of moving targets[J].IEEE Trans on AES,1999,35(1):188-200.
[5]钱 江,孙光才,李凉海,等.一种多通道SAR地面快速目标高概率检测方法[J].电波科学学报,2011,26(2):354-361.QIAN Jiang,SUN Guangcai,LI Lianghai,et al.Multi-channel SAR high speed target indication with improved detection probability[J].Chinese Journal of Radio Science,2011,26(2):354-361.(in Chinese)
[6]陶 然,齐 林,王 越.分数阶Fourier变换的原理与应用[M].北京:清华大学出版社,2004.
[7]杜雨洺,杨建宇.基于FRFT的LFMCW雷达加速动目标检测与参数估计[J].电波科学学报,2005,20(6):815-818.DU Yuming,YANG Jianyu.Novel method of moving target detection and parameter estimation for LFMCW radar[J].Chinese Journal of Radio Science,2005,20(6):815-818.(in Chinese)
[8]LIU Yimin,MENG Huadong,LI Gang,et al.Velocity estimation and range shift compensation for high range resolution profiling in stepped-frequency radar[J].IEEE Geoscience and Remote Sensing Letters,2010,7(4):791-795.
[9]王 俊,张守宏.微弱目标积累检测的包络移动补偿方法[J].电子学报,2000,28(12):55-59.WANG Jun,ZHANG Shouhong.Study on the motion compensation of range migration for weak moving target detection[J].Acta Electronica Sinica,2000,28(12):55-59.(in Chinese)
[10]BOERS Y,DRIESSEN J N.Multi-target particle filter track before detect application[J].IEE Proceedings of Radar Sonar Navig,2004,151(6):351-357
[11]KRAMER S A.Doppler and acceleration tolerances of high-gain,wideband linear FM correlation sonars[J].Proceedings of the IEEE,1967,55(5):627-636.
[12]DOISY Y,DERUAZ L,BEERENS S P,et al.Target Doppler estimation using wideband frequency modulated signals[J].IEEE Trans on Signal Processing,2000,48(5):1213-1224.
[13]沈显祥,叶瑞青,唐 斌,等.基于欠采样的宽带线性调频信号参数估计[J].电波科学学报,2007,22(1):43-46.SHEN Xianxiang,YE Ruiqing,TANG Bin,et al.An algorithm for estimation of wideband LFM signal parameters based on subsampling[J].Chinese Journal of Radio Science,2007,22(1):43-46.(in Chinese)
