预应力超高强混凝土梁弹性刚度分析＊

2013-03-09

武汉理工大学学报（交通科学与工程版） 2013年1期

（大连理工大学港口和近海工程国家重点实验室大连 116024）

0 引言

随着桥梁工程技术的不断发展，大跨度、超高强装配式后张法预应力混凝土桥梁被广泛应用于公路工程建设项目中［1］，但是我国新颁布的规范《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62－2004）适应的混凝土强度等级为C15～C80［2］，然而随着混凝土技术的发展，比规范混凝土强度等级更高的超高强混凝土在实际工程中已逐渐得到应用及推广．在应用超高强混凝土时，现行混凝土桥涵设计规范规定的弹性刚度折减系数是否适用或需要修订是一个迫切需要研究却一直未得到有效解决的问题．因此，可通过对预应力超高强混凝土梁的试验研究，对其弹性刚度进行详细分析．

混凝土应变的观测，由于张拉端锚具变形和预应力筋内缩损失导致预应力的衰减，对有效预加应力产生重大影响，因此张拉过程中在试验梁的受压区粘贴混凝土应变片，以监测张拉过程中混凝应变的变化，并根据材料力学公式，求得有效预加应力；反拱值测量，在张拉工程中，对试验梁进行变形测量，并结合有效预加应力和材料力学理论，寻求反拱值与刚度之间的变化关系．

1 试验基本情况

试验共对9根后张法预应力超高强混凝土简支梁进行张拉阶段的受力监测，截面尺寸为160 mm×340mm，混凝土标号为C100，弹性模量为5．28×104N／mm2，普通纵向受力钢筋采用HRB335级钢筋，箍筋为HPB235级钢筋，弹性模量为2．1×105N／mm2，预应力筋采用1860级钢绞线，弹性模量为1．95×105N／mm2，张拉控制应力均为0．75fptk（fptk为预应力筋抗拉强度标准值），直径分别为15．2mm和12．7mm，预应力锚具采用低回缩锚具，梁长L＝1．2，1．4，1．6m．梁的截面尺寸见图1，低回缩锚具见图2，配筋情况见表1．

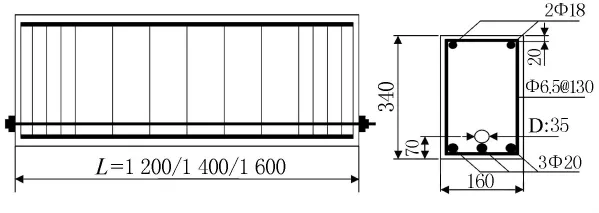
图1 试验梁的配筋图（单位：mm）

在张拉过程中用标距为100mm的混凝土应变片测试受压区的混凝土应变，并分别在梁的两端以及中间安装LVDT，设两端读数分别为a和b，中间的读数为c，见图3，那么反拱值计算式为f＝c－（a＋b）／2，利用IMC数据采集仪采集混凝土应变和反拱值．

图2 低回缩锚具

表1 试验梁的设计参数

图3 试验梁测点图

2 预应力超高强混凝土梁刚度分析

根据文献［3］，影响构件截面刚度的弯矩分为2部分，即M＝M0＋M1．式中：M0为有效预加应力产生的弯矩；M1为试验梁自重产生的弯矩．由于试验梁的自重较小，可以忽略不计，因此：M＝M0．

2.1 有效预加应力的计算

根据测试得到的混凝土受压区应变值，可获得预应力超高强混凝土梁的有效预加应力为［4］

式中：Np为预应力超高强混凝土梁的有效预加应力；A0为试验梁换算截面面积；I0为试验梁换算截面惯性矩；ep0为换算截面重心至预加力作用点的距离；y0为换算截面重心至所计算纤维处的距离；ε为计算纤维处混凝土的应变值；Ec为混凝土的弹性模量．

2.2 刚度折减系数计算

由于Np是考虑第一批预应力损失的预应力钢筋合力，因此试验梁在施加预应力后，在不考虑梁体自重的情况下，得出作用在预应力超高强混凝土梁上的弯矩为［5］

预应力超高强混凝土梁反拱值为

式中：α为弹性刚度折减系数；Mx为跨中作用单位力时任意截面处所产生的弯矩值；B＝EcI0．

将式（1），（2）代入式（3）得

3 刚度折减系数的计算

本次试验梁的预应力采用两次张拉的方法，首次张拉预应力为1．05σp（σp＝0．75fptk），然后逐渐放张，再次张拉到1．05σp时，拧紧低回缩锚具的螺环．同时监测两次张拉后试验梁的反拱值和混凝土应变．并将混凝土应变值代入式（1）中，求出预应力筋的有效预加应力，将有效预加应力转换为等效荷载，并将梁体的反拱值和等效荷载产生的弯矩代入式（4）中便可求得梁体弹性刚度的折减系数．计算结果见表2．

表2 弹性刚度折减系数计算结果

由表2可见，第二次张拉后的预加应力均大于第一次张拉后的预加应力，增幅为42．6%～68．8%，说明采用低回缩锚具能够有效降低由于张拉端锚具变形和钢筋内缩导致的预应力损失．本文试验得到的预应力超高强混凝土梁的弹性刚度折减系数为0．998～1．089，而文献［6］根据全预应力混凝土梁的试验结果得到的弹性刚度折减系数在0．91～1．06之间，通过对比可以看出，本文试验得到的弹性刚度折减系数略大于文献［6］的试验值，这主要是因为本文试验梁所采用的超高强混凝土的弹性模量显著大于普通混凝土的弹性模量，本文得到的试验梁的弹性刚度折减系数平均值¯X＝1．031 556，若取保证率为95%，则有