柴油机油底壳声液振耦合系统噪声模态研究＊

胡启国 李力克 陈万德

（重庆交通大学机电与汽车工程学院1） 重庆 400074）

（川庆钻探工程公司安检院泸州环监所2） 泸州 6460001）

柴油机具有良好的燃油经济性、动力性、排放性，但柴油机工作粗暴，产生的噪声振动相对较大．在对G12V190系列柴油机噪声测量中，最大噪声值达到了118dB（A），最大振动加速度为13 m／s2．过大的振动会降低机器的使用寿命，过高的噪声会对操作人员的身心健康产生严重的影响．在发动机的结构噪声辐射中，结构薄壁件产生的辐射噪声占总噪声的50%左右，而油底壳产生的噪声占总量的20%左右［1］．油底壳一般由薄钢板冲压而成，在曲轴箱的振动时辐射出大量噪声．早期的分析研究油底壳振动噪声只考虑油底壳结构方面的影响参数，而并没有考虑机油和内部空腔的影响，这显然与实际情况有着较大的差异．

本文利用有限元及多模型耦合的方法对G12V190系列柴油机油底壳壳体与内部润滑油和腔体系统的声学特性进行深入的研究，从而为进一步降低柴油发动机的噪声提供依据．

1 有限元声液振耦合方程

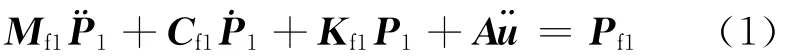
在声液振耦合系统中油底壳内部空腔声场离散形式的波动方程为［2］式中：Mf1为等效声学质量矩阵；Cf1为等效流体阻尼矩阵；Kf1为等效声学刚度矩阵；P1为节点声压矩阵；A为声和油底壳的耦合矩阵；为单元节点位移对时间的二阶导数矩阵；Pf1为由于油底壳振动而作用在空腔声场上的载荷．

在润滑液与油底壳作用的耦合区，流体的振动对油底壳内表面产生压力，油底壳的振动同样会引起润滑液的扰动，为流体提供速度和加速度．

式中：Mf2，Cf2，Kf2为润滑液流体的质量、阻尼、刚度矩阵；P2为流体对应节点的声压矩阵；Pf2为作用在润滑液上的载荷；R为流固耦合矩阵；为固体单元节点位移对时间的二阶导数矩阵．

在油底壳声、液、振耦合分析中，忽略掉声压、液体的影响时油底壳结构振动的方程为

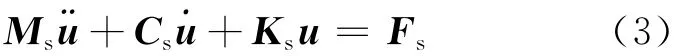
式中：Ms为油底壳结构质量矩阵；Cs为结构阻尼矩阵；Ks为结构刚度矩阵；u为结构位移矩阵；Fs为油底壳外激励矩阵．

在声、液、振耦合系统中，不但要考虑油底壳的外激励，而且还要考虑空腔声压、润滑液压力对油底壳振动的影响，所以需要在结构与润滑液和空腔的接触面上加上润滑液和空腔的压力载荷．此时结构振动方程为

方程（1）、（2）、（4）描述声 －液－结构振动耦合系统运动方程，用统一的矩阵形式表示如下．

2 声液振耦合系统模态分析

2.1 油底壳结构的模态分析

为了研究需要，对油底壳的模型做了简化，省略了放油口和一些板筋．在ABAQUS中利用四面体单元进行网格的划分，并计算出油底壳在自由状态下的振动模态参数，包括振动频率及对应的振型，同时利用锤击法对油底壳进行实验模态参数求解．网格的尺寸取0．015m，油底壳的材料取蠕墨铸铁，弹性模量为1．45×105MPa、泊松比为0．33、密度为7 800kg／m3，建立油底壳结构有限元模型见图1．

图1 油底壳有限元模型

利用ABAQUS对油底壳结构有限元模型模态分析计算，得到自由状态下油底壳结构模态固有频率值与利用实验得到的油底壳结构模态固有频率值对比如表1所列，由于本文所研究的振动频率范围在40～1 000Hz，计算列出了前20阶的模态．

由表1可见，计算模态和实验模态误差保持在5%以内，所以建立的模型精度较高，计算的结果具有较高的可靠性．

取油底壳1阶、2阶模态振型图如图2所示．通过模态振型图对比，第1阶、2阶固有频率下油底壳振幅相对较大．固有频率较低时的振幅度比高频振动幅度大，并且振动较大的区域随着频率的增加由油底壳的边缘向底部扩散．当油底壳受到外界的激励，这些模态被激起时容易产生共振，从而导致油底壳产生比较强的辐射噪声．

表1 油底壳前20阶自由模态

图2 油底壳模态振型图

2.2 油底壳中润滑油声学模态分析

润滑油作为一种流体，密度为886kg／m3，声音在润滑油中传播的速度为1 324m／s，对于润滑油有限元模型网格的划分满足最大单元边长小于计算频率最短波长的1／6［3］，由于本文所研究的噪声频率范围在40～1 000Hz所以划分网格的最大边长取0．02m，假设油底壳外部为刚性壁面，同时用Hypermesh对润滑油进行网格划分，将划分后的模型导入SYSNOISE中进行声学模态分析计算，算出前10阶模态，如表2所列，图3给出了油底壳润滑液部分声学模态的振型图．

表2 润滑油声学前10阶模态

图3 油底壳润滑油声学模态

本文所研究的噪声频率主要在40～1 000 Hz，所以只考虑前3阶模态对耦合的影响．1阶声学模态为频率为0Hz，即1阶油底壳润滑油声场声压处处相等，声场声压分布云图见图3．

由图3可见，声压较大的区域多集中在润滑油前后和左右两端，即靠近油底壳刚性壁面的区域，当润滑油的这些地方声学模态被激起的时候会在油底壳的内表面发生声学共振，声压相应增强，耦合后会让油底壳外部的噪声也随之增强．

2.3 油底壳空腔声学模态分析

油底壳内空腔部分为空气，空气的密度为1．21kg／m3，声速为344m／s．对于空气网格的划分根据分析频率而定，网格划分的大小同样满足最大单元的边长小于计算最短波长的1／6．根据本文所关心的噪声频率为40～1 000Hz声学网格的最大边长选取为0．02m，网格的类型为四面体单元．将划分后的油底壳空腔模型导入SYSNOISE中进行声学模态分析计算，计算油底壳空腔前20阶声学模态如表3所列．

表3 油底壳空腔前20阶声学模态

图4为油底壳空腔部分声学模态振型图．

由图4可见，频率较低时空腔内部振型较大，频率较高时振型相对较小．固有频率较低时主要振动区域集中在前段，油底壳前段区域的声压较大；固有频率相对较高时主要振动区域集中在油底壳的两端，油底壳两侧声压相对较大，并且油底壳内部空腔声压节线的分布具有一定的跳跃性．

2.4 声液振耦合模态分析

上文中建立的油底壳结构有限元模型为刚性的，但在实际情况下油底壳壁面是弹性的，边界的变化会造成润滑油和空腔声学模态频率的变化，这种声液固耦合作用带来的模态变化会对总体的噪声产生巨大的作用，为了更为准确的进行声学模态分析，要对声、液、振耦合的模型进行模态分析．

图4 油底壳内部空腔声学模态

本文所研究的对象为油底壳的声－液－振三者耦合模态，耦合变量多，且耦合矩阵非对称．若用方程式（4）直接计算，计算过于复杂，因此采用模态法，可以简化计算，节省计算时间［4］．利用模态叠加法计算油底壳耦合系统模态，变换如下［5］．

式中：Φs为没有耦合情况下的结构模态；Φf1为没有耦合的情况下空腔与刚性壁面接触的声学模态；Φf2为没有耦合情况下润滑油与刚性壁面接触处声学模态．ξs，ξf1，ξf2为对应模态参与因子，将式（6）～（8）代入方程（4）得到模态耦合方程

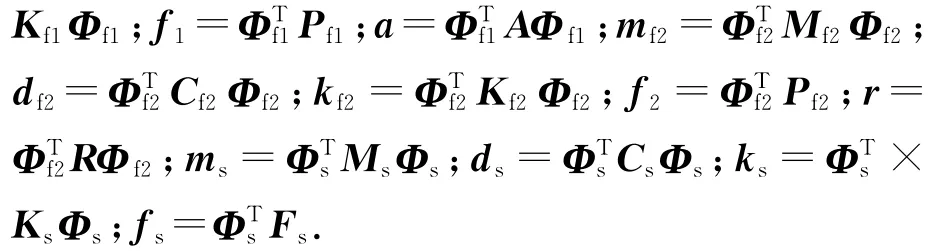
将油底壳空腔声学有限元模型、润滑油声学有限元模型、油底壳结构有限元模型导入SYSNOISE中进行流－固耦合模态分析，在耦合面上所有的结构单元节点与声学有限元节点相对应，通过方程（9）的理论推导及声学有限元软件的分析计算，得到耦合系统前28阶模态固有频率，见表4所列．

表4 油底壳声学耦合模态结果

通过表4、表3、表2、表1对比可知，声、液、固耦合系统模态频率比空腔声学模态频率略微偏小．与润滑油声学模态相比，耦合情况下的模态频率基本上没什么变化．与油底壳自由模态相比，耦合情况下模态频率变大．

从模态频率振型图5可以清楚地看出，耦合系统与油底壳模态、润滑油的模态、空腔的模态有比较强的关联性．耦合系统的模态有部分是因为油底壳振动引起声压变化而产生的，还有一部分是因为油底壳空腔声压的变化引起了油底壳振动而产生的．在耦合系统模态频率中，前半部分的模态频率接近油底壳空腔声学模态频率，后半部分接近油底壳结构模态频率．在118．26Hz附近耦合系统模态振型见图5．

图5 固有频率118．26Hz声学耦合模态振型

在低频范围内，润滑油对耦合系统模态影响相对较小．油底壳结构模态和空腔声学模态在一些频率上是接近，这种情况可以认为是强耦合模态［6］．当激励的频率与这些耦合频率相重合，由于强耦合的效应，油底壳壁板的振动以及内部润滑油、空腔的声压波动幅值会加大，进而出现共振现象，这时油底壳外部会出现强烈的辐射噪声．如果外部激励频率偏离耦合系统固有频率，这时油底壳共振难以被激起，进而向外的噪声辐射也会相对较弱［7－11］．

3 G12V190柴油机油底壳耦合系统声学特性验证分析

对G12V190柴油机油底壳进行振动的测量频谱分析见图6所示．

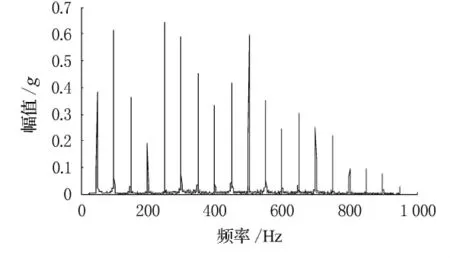
图6 油底壳振动加速度频谱图

从频谱图中可以看出在118Hz附近油底壳的振动加速度值仅次于300Hz左右的加速度值，说明在118Hz耦合模态强振型被激起，油底壳壁板的振动以及内部润滑油、空腔的声压波动的幅值相应的也加大了，此时油底壳的振动以及向外辐射的噪声也相应的变大．当外部的激励频率偏离了耦合系统的频率时，振动比较弱，相应的向外辐射噪声值也比较的小．

4 结 论

1）柴油机油底壳固有频率较低时的振动幅度比高频振动幅度大，并且振动较大的区域随着频率的增加由油底壳的边缘向底部扩散．

2）柴油机油底壳中的润滑液声压较大的区域多集中在润滑油前后和左右两端，即靠近油底壳刚性壁面的区域，当润滑油的这些地方声学模态被激起的时候会在油底壳的内表面发生声学共振．

3）油底壳声液振耦合系统强耦合模态固有频率在118．26Hz左右，耦合模态强振型被激起，油底壳壁板的振动以及内部润滑油、空腔的声压波动的幅值最大．

4）在频率较低时，由于润滑油声学固有频率相对较高，所以油底壳润滑油声学模态对耦合系统模态影响相对较小，而油底壳和内部空腔的模态频率和振型展现出了对声液振耦合系统有很强的相关性．油底壳耦合系统特性在频率较低时主要是由空腔声压变化来决定的，频率较高时是由润滑油、空腔、油底壳结构模态频率和振型共同决定耦合系统模态．

［1］马大猷．噪声控制学［M］．北京：科学出版社，1984．

［2］陈福忠，项昌乐，刘 辉．车辆变速箱声振耦合系统的声学特性研究［J］．噪声与振动控制，2011（1）：25－20．

［3］左言言，方玉莹．拖拉机驾驶室模型的声学灵敏度分析［J］．农业工程学报，2005（3）：126－128．

［4］KIM S K，LEE J M，SUNG M H．Structure－acoustic coupled analysis and application to noise reduction in a vehicle passenger compartment［J］．Journal of Sound and Vibration．1999，225（5）：989－999．

［5］章宗鹏，张 艺，曾革委．舱段结构流固耦合声振特性的模态叠加法研究［J］．振动工程学报，2004，8（17）：806－808．

［6］ABBES S M，BOUAZIZ S，CHAARI F，et al．An acoustic－structural interaction modeling for the evaluation of a gearbox－radiated noise［J］．International journal of Mechanical Scinces，2008（50）：569－577．

［7］郭 磊，郝志勇，贾维新．预测与降低柴油机油底壳辐射噪声方法研究［J］．汽车工程，2006（7）：285－287．

［8］袁兆成．降低车用柴油机振动噪声的设计方法［J］．农业机械学报，2004，6（3）：48－52．

［9］张林仙，樊文欣，张保成．含油量对油底壳固有频率的影响研究［J］．车用发动机，2006，8（4）：66－68．

［10］冯 威，袁兆成，刘伟哲．机油参数对液固耦合油底壳辐射声场的影响［J］．振动与冲击，2006，1（1）：151－153．

［11］金广文，缪旭弘，匡贡献，等．基于工作模态参数辨识的水下复杂结构模态分析方法［J］．武汉理工大学学报：交通科学工程版，2011，35（2）：285－288．