基于混沌云粒子群算法的交叉口信号智能配时优化＊

（大连理工大学建设工程学部 大连 116024）

0 引 言

目前，国内外有关学者对信号配时方法进行了深入研究，王海起［1］等利用遗传算法、粒子群等智能算法，建立了以车辆延误最小为控制目标的交通信号配时模型，配时效果优于传统的定时控制和交通感应控制［2］．但此类方法大多以 Webster［3］的车辆延误作为控制目标，而高峰时段实际车辆延误时间比Webster计算延误时间要长，因此，仅以延误时间作为唯一的控制目标是远远不够的，Bullock［4］、徐勋倩［5］、瞿高峰［6］等以交叉口延误、停车次数最小和通行能力最大为控制目标，配时效果优于单一车辆延误或停车次数为优化目标的配时模型，但上述方法控制优化函数在一天内保持不变，并不能反映变化的交通流对控制函数的影响．李晓娜［7］等建立了基于不同优化目标的控制模型，不能反映高峰时段车流激增对车辆延误和停车次数计算的影响，依此进行交叉口信号配时优化，不能保证交叉口信号配时方案的综合最优．

本文基于猫Cat映射和云模型，针对PSO算法的不足，对PSO算法进行改进，提出了混沌云粒子群算法（chaos cloud particle swarm optimization，CCPSO），建立了基于CCPSO算法进行求解的交叉口信号配时模型，最后，结合实测交通流数据进行数值实验，通过模型对比验证提出算法及模型的有效性和先进性．

1 交通信号配时模型

1.1 交叉口交通信号控制问题的描述

1）交叉口第i相位车辆平均延误

4）加权系数的设计 设第i相位车辆延误、停车率和有效通行能力的加权系数分别为，和，按文献［5］得到和计算公式为

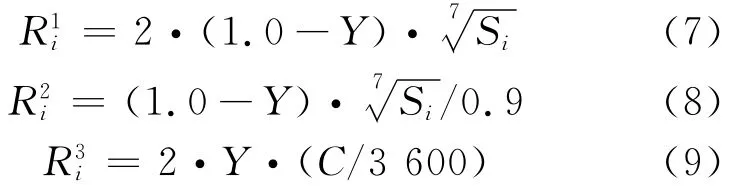
式中：Si为第i相位饱和流量，pcu／h；Y 为交叉口的流率比．

1.2 交叉口交通信号智能动态配时模型

考虑信号控制的损失和效益，以车辆延误和停车次数最小和通行能力最大作为目标函数，利用可随交通量实时变化的加权系数R1i，R2i和R3i把这3个目标统一为单目标函数，建立交叉口交通信号实时动态配时模型如下．

式中：gmin和gmax为交叉口第i相位的最小有效绿灯时间和最大有效绿灯时间，一般取值为15s和90s；Cmin和Cmax为交叉口最小周期和最大周期，一般取值为80s和300s；li为第i相位损失时间，一般取值为3～5s；n为交叉口相位数，本文中n取4；k1和k2为交叉口交通流状态智能选择参数；智能选择参数k1和k2的引入，使得提出的信号配时方案优化模型具备了自主根据交通流状态选择相应车辆延误和停车率计算公式的能力，提高了模型的智能性和泛化性能．

2 混沌云粒子群算法

本文针对粒子群算法的不足，基于Cat映射理论和云模型对标准粒子群算法进行改进．首先利用Cat映射初始化父代群体，当群体适应度方差小于in时，利用正态云模型对全局最优位置进行小生境局部细微搜索，当达到一定次数小生境局部细微搜索［8］，而全局最优位置仍不能满足终止准则时，利用Cat映射对全局最优位置进行全局混沌搜索．

基于CCPSO算法求解交叉口交通信号配时模型的步骤如下．

步骤1 参数初始化．设定粒子群规模N，Cat映射的迭代次数M，加速常数c1和c2，最大进化代数Gmax，最优个体适应度值变化率E，适应度方差最小值Q2min，全局最大搜索次数Goverall－max，局部最大搜索次数Gpart－max，令当前进化代数为G＝1，全局搜索识别参数NEEDoverall＝0．

步骤2 Cat映射群体初始化．根据Cat映射初始化父代粒子的位置，并随机初始化速度．

步骤3 适应度评价．将每个粒子的各维向量作为信号配时模型的参数，结合具体交通流量，按式（10）计算综合优化目标，作为相应粒子的适应度值fi，计算第i个粒子历史最优位置Pki和全局最优位置Pkg．

步骤4 搜索终止判断．判断当前全局最优个体Pki是否满足终止准则，若满足转入步骤9，否则转入步骤5，进化代数G＝G＋1．终止准则采用最大进化代数Gmax与相邻进化代数最优个体适应度值变化率E相结合．

步骤5 自适应惯性权重．根据文献［9］策略计算动态自适应惯性权重因子ω．

步骤6 更新粒子速度和位置．更新粒子群每个粒子的速度和位置，计算所有粒子的适应度值，更新第i个粒子历史最优位置和全局最优位置．

步骤7 云模型小生境局部搜索．按式（11）［10］计算当前群体的适应度方差δ2，若δ2＜，根据云模型［13］对全局最优个体进行小生境局部搜索，判断是否满足搜索终止准则，若满足转入步骤9，否则令NEEDoverall＝1（NEEDoverall为全局搜索识别参数，用于判断是否进行全局搜索）转入步骤8．

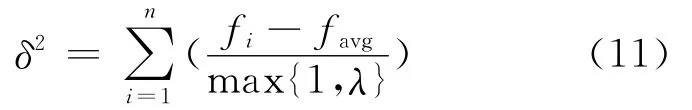
式中：λ＝max（｜fi－favg｜）；f为归一化定标因子，N粒子群总数；fi为第i个粒子的适应度值；favg为粒子群目前的平均适应度值．

步骤8 Cat映射全局混沌搜索．若NEEDoverall＝1，则根据Cat映射完成全局混沌搜索，令NEEDoverall＝0，判断当前全局最优个体Pkg是否满足终止准则，若满足转入步骤9，否则转入步骤6．

步骤9 输出全局最优值Pkg作为优化后的最优配时方案．

3 实例验证与分析

3.1 实验设计

本文基于大连市联合路和长江路交叉口的实测数据进行数值试验，采用四周内路口感应线圈在平峰时段I（09：30～11：00）、平峰时段II（14：00～16：00）、高峰时段I（07：00～09：00）和高峰时段II（17：30～19：00）的实测车流量的均值作为状态的驶入流量，每一相位的交通信号配时由各个相位关键车道的交通流量作为该相位的控制流量，各相位控制流量比及各相位的饱和流量如表1所列．交叉口各相位的最小有效绿灯时间gmin和最大有效绿灯时间gmax分别取为15s和90s，最小周期Cmin和最大周期Cmax取值为80s和300s，各相位损失时间li均取为5s．

表1 各相位控制流量比及相位饱和流量

3.2 算法性能分析

为验证本文提出的CCPSO算法的有效性，以高峰时段I的交通流量数据为例，采用本文CCPSO算法与文献［6］中的粒子群算法（PSO）、文献［11］中的基于Logistic映射的混沌粒子群算法（CPSO）和文献［12］中的基于云模型的云变异粒子群算法（CHPSO）4种算法，分别对高峰时段I的交通信号的配时方案进行求解，计算机数值计算利用 Matlab 7．1编制程序，运行环境为：Core（TM）2CPU，1．81MHz，2GB内存的微机，操作系统WindowsXP．

考虑到算法参数的设置不同也会影响算法性能，因此4种算法除需要特殊设置的参数外，其他参数均采用相同标准，算法种群规模N＝50；最大进化代数Gmax＝200；最优个体适应度值变化率E＝0．000 1；C1＝C2＝2．0；Cat映射的迭代次数M＝200；适应度方差最小值δ2min＝1．5；全局最大搜索 次 数 Goverall＿max＝10；局 部 最 大 搜 索 次 数Gpart＿max＝10；4种算法各运行50次，得到200代内平均最大适应度值变化曲线如图1所示．

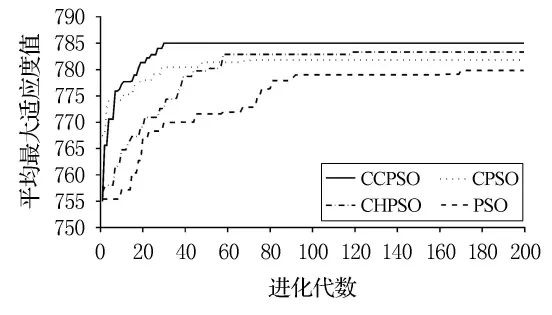
图1 4种算法进化曲线

由图1分析得出，在200代进化过程中，采用Cat映射初始化父代群体的CCPSO算法和CPSO算法，在迭代初期搜索到的粒子的平均最大适应度值明显高于PSO算法和CHPSO；而基于Cat映射初始化和全局混沌搜索以及利用正态云模型进行小生境局部搜索的CCPSO算法，即克服了PSO易陷入局部最优解的不足，又增加了对最优解小生境进行细粒度搜索，加速了最优解的搜索速度，提高了解的精度，从而使CCPSO算法取得了更好的优化效果．

3.3 控制效果分析

为验证本文建立的交叉口交通信号动态配时模型的控制效果，同时选用文献［2］中的经典Webster算法的配时模型、文献［6］中基于PSO的交通信号配时模型和本文提出的模型，对平峰时段和高峰时段的交通信号的配时方案分别进行优化，3种模型优化得到的配时方案及性能指标对比结果统计如表2所列．

表2 Webster算法、PSO和CCPSO算法的性能指标比较

通过以上对比分析得出：基于PSO和CCPSO算法进行优化的配时模型在平峰时段和高峰时段的配时方案与传统的Webster模型相比，取得了更好的优化效果；在平峰时段，基于PSO和CCPSO算法的配时模型在保证停车次数和交叉口的通行能力小范围变化的前提下，降低了车辆延误，提高了通过交叉口时的舒适度；在高峰时段，基于PSO和CCPSO算法的配时模型在降低车辆延误和停车次数的同时，有效提高了交叉口的通行能力，增强了交叉口的使用效率，说明基于PSO和CCPSO算法的配时模型用于高峰时段的信号配时可取得更好的配时效果；而在基于PSO和CCPSO不同算法的配时模型的对比方面，基于本文提出的CCPSO算法的配时模型取得了更优的效果．

4 结束语

本文对交叉口交通信号的配时方法进行了研究，新的交叉口交通信号配时方法中，车辆延误和停车次数的计算公式可随交叉口状态的变化而变化，提高了配时模型中车辆延误和停车次数计算的准确度，完善了现有配时模型在计算车辆延误和停车次数过程中采用单一计算公式的不足；提出了CCPSO算法；建立了基于CCPSO进行优化的交叉口信号配时模型．实例计算结果表明：在算法性能方面，提出的CCPSO算法，提高了粒子种群的多样性，增强了算法的全局和局部搜索能力，改善了PSO算法易陷入局部极小的不足，应用于配时模型的优化，提高了配时模型的泛化性和鲁棒性．在控制效果方面，新的配时模型能够根据交叉口的状态智能调节各性能指标权重，对各个指标进行选择性优化，有效减少了车连延误和停车次数，提高了交叉口的通行能力，实现了管理效益和使用效率综合最优．今后可将本模型拓展应用于多交叉口和整个交通网络信号的智能控制中．

［1］王海起，王劲峰．一种基于粒子群的交通信号离线配时优化方法［J］．计算机工程与应，2008，44（11）：13－17．

［2］全永燊．城市交通控制［M］．北京：人民交通出版社，1989．

［3］HALIM C，MIEHAEL G H．Tarffic signal timing optimization based on genetic algorithm proach inluding drivers routing［J］．Tnarsportation Research PartB，2004，38（2）：329－342

［4］BULLOCK D，URBANIK T．Traffic signal systems addressing diverse technologies and complex user needs，A3A18［R］．Washington D C：Committee on Traffic Signal Systems，1999．

［5］徐勋倩，黄 卫．单路口交通信号多相位实时控制模型及其算法［J］．控制理论与应用，2005，22（3）：413－416．

［6］瞿高峰，陈淑燕．粒子群优化算法在交通信号配时中的应用［J］．控制理论与应用，2006，24（4）：256－258．

［7］李晓娜．单交叉口自适应控制方法的研究［D］．大连：大连理工大学，2006．

［8］LI Dey，MENG Haijun，SHI Xueme．Membership clouds and membership cloud generators［J］．Journal of Computer Research and Development，1995，32（6）：15－20．

［9］沈 锡，胡江强，尹建川．一种搜索空间自适应变化的自适应粒子群算法［J］．大连海事大学学报，2011，37（1）：104－107．

［10］吕振肃，侯志荣．自适应变异的粒子群优化算法［J］．电子学报，2004，32（3）：416－420．

［11］孙 湘，周大为，张希望．一种混沌粒子群算法［J］．计算机工程与科学，2010，32（12）：85－89．

［12］张英杰，邵岁锋．一种基于云模型的云变异粒子群算法［J］．模式识别与人工智能，2010，24（1）：91－95．