一种基于邻域空间的混合粒子群优化算法

曾 毅，朱旭生，廖国勇

（华东交通大学基础科学学院，江西南昌 330013）

粒子群优化算法（particle swarm optimization，PSO）是Eberhart和Kennidy1995年开发的一种新的群体智能计算技术［1-2］，源于对鸟群捕食的行为研究。由于PSO算法概念简单，容易实现，只有少数参数需要调整，所以自其被提出以来受到学术界的重视和研究，并广泛地应用于函数优化、神经网络训练、模糊系统控制等领域。

PSO算法是属于有导向的随机性启发式算法。尽管在求解大多数优化问题时表现出色，但在求解高维复杂函数优化问题时，极易陷入局部最优解，进化后期收敛速度及解的精度也不够理想。为此许多学者提出了不少改进算法，Shi和Eberhart提出了惯性权重方法［3-4］，用惯性权重ω来控制前面的速度对当前速度的影响，较大的ω可以加强PSO算法的全局搜索能力，而较小的ω能加强PSO算法的局部搜索能力。该方法加快了收敛速度，提高了PSO算法的性能。但当待解问题很复杂时，在迭代后期全局搜索能力不足，导致不能找到要求的最优解。Clerc提出收缩因子概念［5］，通过引入收缩因子χ，可以有效地控制惯性权重ω和学习因子c1，c2，以确保算法收敛。Kennedy等［6-7］提出几种基本的邻域结构及邻域的动态选择策略，结果表明邻域结构影响算法的性能。Ratnaweera等［8］为改善算法的性能，提出了学习因子c1，c2随时间动态线性调整的策略。文献［9-10］将求解无约束最优化问题的直接法嵌入粒子群优化算法中，加快了算法的收敛速度，提高了解的质量。本文引入邻域空间概念，提出一种基于邻域空间的混合粒子群优化算法（hy⁃brid particle swarm optimization），该算法提出新的粒子速度更新方程，给出学习因子c1，c2非线性调整策略及局部搜索算法嵌入粒子群优化算法的新方法。数值模拟表明新的算法很好地平衡了算法的全局“探索”与局部“开发”，在避免早熟现象的发生、改善迭代后期的收敛速度和解的精度效果明显。

1 标准粒子群优化算法

式（1）（2）为标准粒子群优化算法的在第d(d=1，2，…，n)维上的速度和位置更新方程。

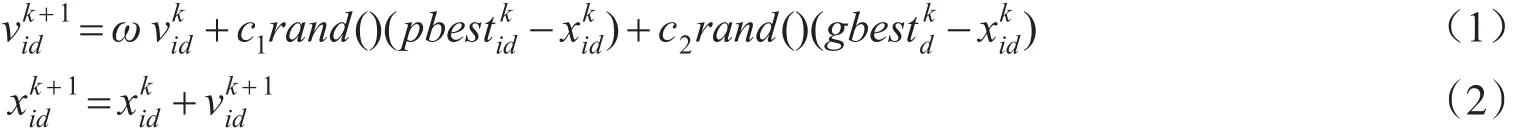
其中：k为进化代数,表示粒子xi在第k代d维上的速度；表示粒子xi在第k代d维上的位置；pbesti表示粒子xi所经历的最好位置；gbest表示群体中所有粒子所经历的最好位置；c1，c2为学习因子，且取非负常数；rand( )是均匀分布于[0，1]之间的随机数；ω为惯性权重，它决定了粒子先前速度对当前速度的影响程度，从而起到平衡算法全局和局部搜索能力的作用。

2 基于邻域空间的混合粒子群优化算法

2.1 算法思想

粒子间的信息共享是PSO算法的基础，而利用哪些信息，如何利用信息则是信息共享机制的核心问题。在标准粒子群优化算法中，所有粒子进化过程中仅共享当前种群中最优粒子的信息，而忽略了其它次运行获得的最优信息。这种信息共享策略使算法在进化后期局部开发能力较强，而全局探索的能力却较弱。一旦粒子赶上种群最优，粒子会聚集到相同位置并停止移动，种群的多样性会逐渐丧失，从而导致“早熟”现象的发生。粒子在寻求共同认识的过程中，粒子会保留自己的最佳信息，也应考虑同伴的信息，当粒子获得优于自己的同伴信息时，就会参考同伴信息，更新自己的最佳信息。这表明粒子的同伴信息的共享可提供了进化的优势。基于以上分析，我们先给出邻域空间概念，然后提出新的更能反映信息共享机制的粒子速度更新方程以及局部优化算法嵌入粒子群优化算法的新方法。

定义1在第k代粒子群中，与粒子xi欧氏距离最近的num个粒子的集合称为粒子xi的邻域空间［12］。

定义2在第k代粒子群中，随机选择的num个粒子的集合称为粒子xi的邻域空间［12］。

本文将粒子xi速度更新方程修改：

岭南建筑在色彩选择上往往喜爱用比较明朗的浅色淡色，同时又喜用青、蓝、绿等纯色作为色彩基调，这些都能使建筑物减少重量感，从而造成建筑外貌的轻巧。同时从岭南传统建筑的装饰、装修、纹样、图案中，提取符号，再将其抽象化，运用到建筑设计中。

其中：plbesti为粒子xi迄今为止所搜索到的最好的邻域极值；c1，c2仍称为学习因子，且学习因子c1，c2随着进化代数k变化。学习因子c1，c2的取值如下

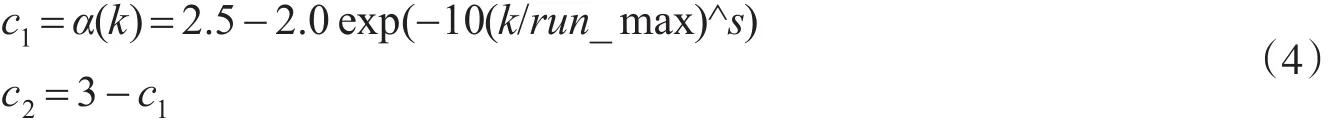
其中：run_max为算法迭代的总次数，s可取大于1的整数，本文取s=5。在整个迭代过程中，学习因子c1从2.5非线性逐渐递减至0.5，而学习因子c2从0.5非线性逐渐递增至2.5。迭代初期，学习因子c1取值较大，学习因子c2取值较小，算法强调粒子共享邻域空间的局部信息，体现局部优化的特性；而在进化的后期，学习因子c1取值较小，学习因子c2取值较大，算法强调粒子共享种群中最优粒子的信息，体现全局优化的特性。

2.2 模式搜索算法

在智能优化算法研究中，人们发现单靠一种算法往往无法保持探测（exploration）和开发（exploitation）的平衡，从而影响了算法的性能，所以人们想到了将两种算法或者多种算法混合在一个模型当中，使混合的算法能充分发挥各种算法的优点，起到提升算法的性能的目的。

模式搜索算法由Hooke和Jeeves于1961年提出的，一种不需要计算导数的无约束最优化的直接算法［13］。算法主要由探测移动和模式移动过程组成，探测移动是沿坐标轴方向的移动，模式移动则是沿相邻两个探索点连线方向上移动，两种移动交替进行，顺着函数值下降的最佳方向搜索到函数的最小值。模式搜索算法的步骤［14］：

Step1：给定初始点x(1)∈Rn，n个坐标方向e1，e2，…，en，初始步长δ，加速因子α≥1，缩减率β∈(0，1)，允许误差ε＞0 ，置y(1)=x(1)，k=1，j=1；

Step2：如果f(y(j)+δej)＜f(y(j))，则令y(j+1)=y(j)+δej，进行Step4；否则，进行Step3；

Step3：如果f(y(j)-δej)＜f(y(j))，则令y(j+1)=y(j)-δej，进行Step4；否则，令y(j+1)=y(j)+δej，Step4；

Step4：如果j＜n，则置j:=j+1，转Step2；否则，进行Step5；

Step5：如果f(y(n+1))＜f(x(k))，则进行Step6；否则，进行Step7；

Step6：置x(k+1)=y(n+1)，令y(1)=x(k+1)+α(x(k+1)-x(k))，置k:=k+1，j=1，转Step2；

Step7：如果δ≤ε，则停止迭代，得点x(k)；否则，置δ:=βδ，y(1)=x(k)；

x(k+1)=x(k)，置k:=k+1，j=1，转Step2。

如何使混合优化算法能充分发挥模式搜索算法强大的局部“开发”能力，又有效地克服模式搜索算法对初始值敏感、易陷入局部最优的缺点。目前，通用的一个做法是以最优粒子为初值进行模式搜索，并将搜索到的新位置替代粒子原来位置，但这种算法对高维多峰函数优化问题的全局寻优能力并不理想。考虑到粒子群优化算法粒子的“聚集”特性，若粒子xkj的位置是第k代粒子群中m个粒子的邻域极值，则m越大，表明xkj所在的位置附近存在最优解可能性越大。以这样的粒子为初值进行局部搜索就应该比较容易找到问题的最优解。为此，在粒子群优化算法中嵌入模式搜索算法的条件是，若K为某一给定正整数，粒子xkj的位置是m个粒子的邻域极值，且m≥K，则以粒子xkj为模式搜索算法的初值进行深度开发。

2.3 混合粒子群优化算法步骤

算法具体步骤：

Step1：设置模式搜索算法和粒子群优化算法的参数，初始化种群中各粒子的位置和速度；

Step2：评价初始种群中粒子，确定每个粒子邻域极值lbest，并将每个粒子邻域极值lbest作为每个粒子的plbest，初始种群中的最佳位置设置为gbest；

Step3：判定粒子是否满足嵌入模式搜索算法的条件，若条件满足，则以该粒子为初值，采用模式搜索算法进行深度开发，并将搜索到的位置和相应的适应值替代粒子开发前的位置和适应值；

Step4：按式（2）（3）更新粒子的速度和位置，评价种群的所有粒子，并更新plbest和gbest；

Step5：若满足算法的终止条件，则输出gbest及其适应值；否则，转step3。

3 实验结果及其分析

为了测试本文提出的混合粒子群优化算法的性能，选取如表1所示的4个全局最优值为0的最小化函数进行仿真实验。混合粒子群优化算法的参数设置见表2，最大速度限制Vmax取为各函数初始范围的上限，惯性权重设置为从0.9到0.4的线性变化。为方便表述，本文的算法1为标准粒子群优化算法，粒子按式（1）（2）更新速度和位置，学习因子c1，c2均取值为2；算法2为基于邻域空间的粒子群算法，粒子按式（2）（3）更新速度和位置，粒子的邻域空间按定义1产生，学习因子c1，c2按式（4）取值；算法3为算法1+模式搜索算法，每代仅对最优粒子进行模式搜索；算法4为算法2+模式搜索算法，每代仅对满足局部搜索条件的粒子进行模式搜索。本文采用Matlab7.1实验平台进行仿真实验。实验结果如表3所示，其中MEAN，BEST、WORST、SD分别表示算法独立运行20次的平均值、最佳适应值、最差适应值和适应值方差，SR表示达到优化目标的寻优次数占实验次数的比例。所谓达到优化目标，是指算法搜索到的测试问题解与问题的最优解之差的绝对值小于1.0×10-4。为了直观地反映算法的寻优效果，图1给出了不同算法对相关测试函数的收敛曲线。

表1 测试函数Tab.1 Test functions

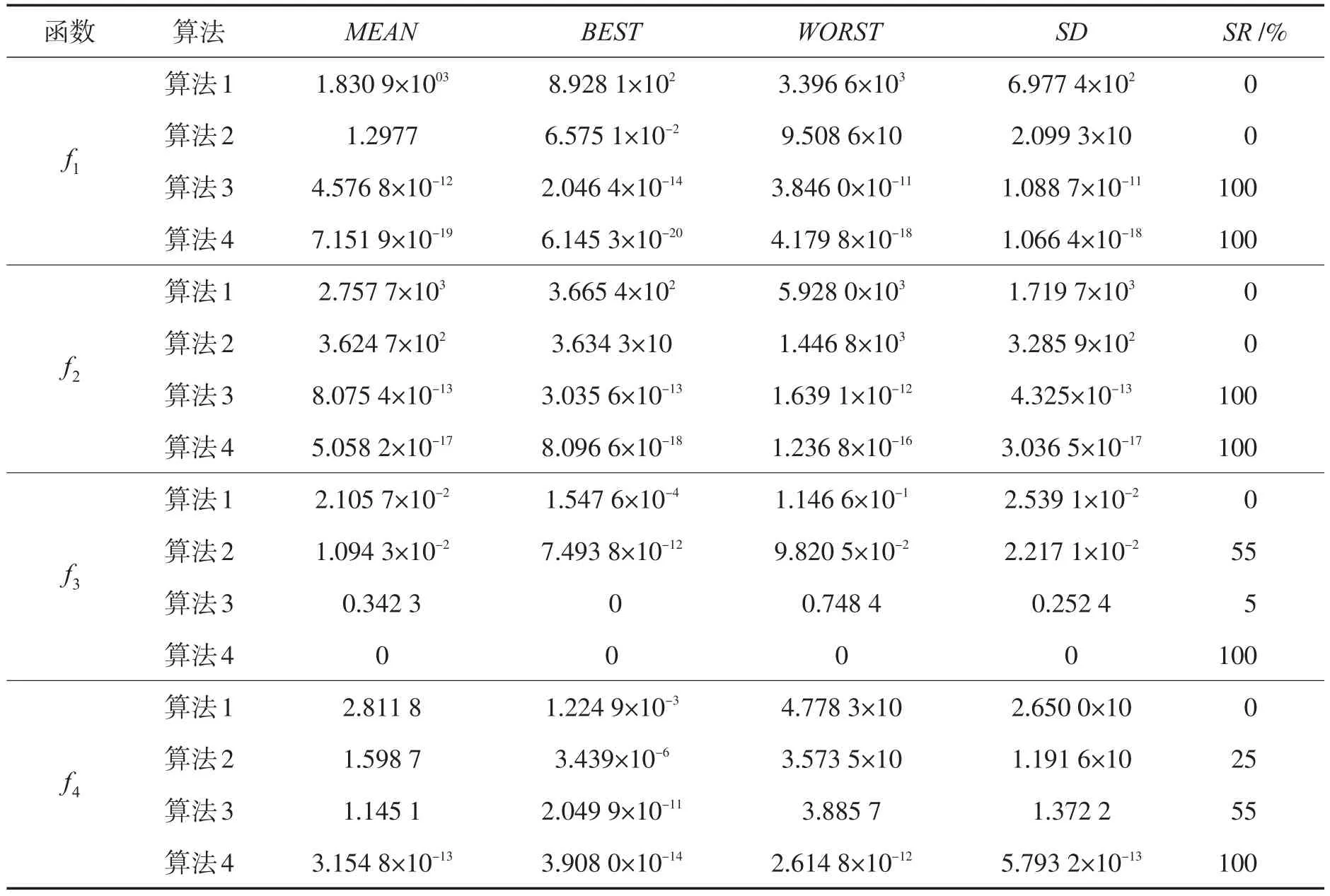
表3 4种算法仿真实验结果Tab.3 Four kindsof algorithm simulation results

图1 测试函数收敛曲线Fig.1 Test function convergence curve

比较表3的数据和图1测试函数收敛曲线，我们得到以下结论：

1）对单峰优化函数而言，算法1和算法2搜索到的最优解的精度都不高，算法2的精度略好于算法1；对多峰优化函数而言，算法2表现出良好全局寻优能力，优化率明显地高于算法1。这主要是算法2在算法初期，学习因子c1取值较大，递减的速度较慢，而学习因子c2取值较小，递增速度较慢，算法更强调粒子共享邻域空间的局部信息，使算法在初期能够在局部范围内进行比较细致的搜索，进而保证算法2搜索到多峰优化函数的全局最优解。算法2在算法后期，学习因子c1取值较小，递减的速度较慢，而学习因子c2取值较大，递增速度较慢，算法强调种群中最优粒子信息的共享，加快算法收敛的速度，提高最优解的精度。但从实际搜索到的最优解来看要真正提高解的精度有必要通过局部优化算法来提升解的精度。

2）对单峰优化函数而言，算法3和算法4搜索到的最优解的精度得到明显的提高，优化达标率均为100%，这表明模式搜索算法提高解的精度的作用是明显的；但对多峰优化函数而言，算法4的全局寻优能力要比算法3强很多。这主要是因为标准粒子群优化算法易于收敛到局部最优解，且跳出局部最优解的能力较弱，对每一代的最优粒子进行模式搜索往往起到提高局部最优解的精度作用，这必然导致算法3的寻优能力不理想；算法4搜索到的最优解的平均值、最佳适应值、适应值方差和达标率都明显地好于算法2搜索到的。这表明每代对满足局部搜索条件的粒子进行模式搜索，使得算法4既能发挥算法2全局寻优能力，又能充分发挥模式搜索算法强大的局部开发能力，并较好地保持这两种能力的平衡。

4 结语

本文提出的基于邻域空间的混合粒子群优化算法较好地解决了粒子群优化算法在求解高维复杂函数优化问题时易陷入局部最优解的问题。新的算法既能充分发挥基于邻域空间的粒子群算法的全局“探测”能力，又能充分发挥模式搜索算法的局部“开发”能力。通过4个典型测试函数的实验研究表明提出算法具有优化精度高、收敛速度快、鲁棒性好，特别适合高维多峰函数的优化问题的求解。在仿真测试的过程中，发现参数num、参数K及两种邻域空间的定义方式都会对算法的性能产生一定的影响，我们继续对这些问题作进一步的研究，并将提出的算法应用于实际问题进一步检测算法的性能。

［1］EBERHARTR C，KENNEDY J.A new optim izer using particle swarm theory［C］//The 6thInt Symp on Micro Machine and Human Science，Nagoya，1995：39-43.

［2］ KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Proc of the IEEE Int Conf on Neural Networks.Piscataway，1995：1942-1948.

［3］SHIY，EBERHARTRC.Amodified particle swarm optimizer［R］.IEEE Internatio-nal Conference of Evolutionary Computation，Anchorage，Alaska，1998.

［4］SHIY，EBERHARTRC.Empiricalstudy of particle swarm optim ization［C］//Proceeding of Congress on Evolutionary Computation.Piscataway，NJ：IEEEService Center，1999：1945-1949.

［5］ CLER CM.The swarm and the queen：towards a determ inistic and adaptive particle swarm optim ization［C］//Proceedings of the Congresson Evolutionary Computation.Piscataway，NJ：IEEEService Center，1999：1951-1957.

［6］ KENNEDY J.Stereotyping：Improving particle swarm performance w ith cluster analysis［C］//Proceedings o f the Congress on Evolut ionary Computing.Piscataway ，NJ：IEEEService Center，2000：1507-1512.

［7］ KENNEDY J，MENDESR.Population structure and particle swarm performance［C］//Proceedings of the 2002Congress on Evolutionary Computation，Piscataway，NJ，USA，2002：1671-1676.

［8］ RATNAWEERA A，HALGAMUGE S K.WATSON H C.Self-organizing hierarchical particle swarm optim izer w ith time-varying acceleration coefficients［J］.IEEETransactionson Evolutionary Computation，2004，8（3）：240-255.

［9］李炳宇，萧蕴诗，汪镭.一种求解高维复杂函数优化问题的混合粒子群优化算法.信息与控制，2004，33（1）：27-30.

［10］贾树晋，杜斌.Rosenbrock搜索与动态惯性权重粒子群混合优化算法［J］.控制与决策，2011，26（7）：1060-1064.

［11］杨维，李歧强.粒子群算优化算法综述［J］.中国工程科学，2004，6（5）：87-93.

［12］巩敦卫，张勇，张建化，等.新型粒子群优化算法［J］.控制理论与应用，2008，25（1）：112-119.

［13］ HOOKE R，JEEVES T A.Direct Search solution of numerical and statistical problems［J］Journal of the Association for Computing Machinery（ACM），1961，8（2）：212-229.

［14］陈宝林.最优化理论与算法［M］.2版.北京：清华大学出版社，2005：333-334.