利用多面函数拟合法解算连续化的深度基准面模型

孙翠羽，马飞虎，陈艳华，崔 迹，李佩华

（1.华东交通大学土木建筑学院，江西南昌 330013；2.国家测绘局海岛（礁）测量重点实验室，山东青岛 266590；3.广岛技术（南京）汽车部件有限公司，江苏南京 211102）

在海洋测绘中，由于平均海面不具有等位的特性，以平均海面为参考的深度基准体系或框架就更加具有复杂性［1-2］。在具体的工程实践中，深度基准面都是以一个或几个验潮站等离散点观测的潮汐数据来确定的。而由于各地的潮汐性质有差异、验潮站潮汐资料获取的时间历元长短不一、各站计算深度基准面时采用的算法不一致等原因，造成各验潮站的深度基准面值不一致［1，3-4］。几十年来，我国虽然已对周边海域进行了广泛勘查和测量，但由于长期缺乏统一高精度的海洋测量基准，一直难以实现各个部门之间及不同时段获得的数据之间的交换和相关图件的拼接，不仅是陆地高程和海洋深度数据不能有效拼接，不同海域不同时期的海图数据也难以融合。两幅相邻的海图在水位归算时按照就近原则采用了不同验潮站的理论深度基准值作为测深数据的起算基准，会造成相同位置的等深线不完全重合等问题。这对沿海测绘、海岸带调查、海岸工程建设以及沿海防潮洪警戒水位的确定等，都会带来不利的影响［5-7］。海图深度基准在实现上的离散性和跳变性，已越来越不能满足实际应用的需求。

海图深度基准面呈点状分布在各地沿岸的长期验潮站处，也就是说按照某种算法求得的海图深度基准面数值仅是对真正曲面形态基准面在特定点的采样。随着验潮技术和测深技术的发展，沿海地区可以获取更多的验潮数据。因此，可考虑采取曲面拟合的方法建立一个渐进性变化的连续的海图深度基准面模型。

曲面拟合是一种常用的技术，在工程、计算机图形、图像以及地球科学等方面有着广泛的应用。目前主要的拟合方法有：多项式曲面拟合法、多面函数拟合法、曲面样条拟合法、移动曲面法以及Kriging拟合法等，本文对多面函数法在实现连续的海图深度基准面模型中的应用作了研究，通过实例分析来探讨其可行性。

1 多面函数拟合法

美国Hardy教授在1971年提出多面函数拟合法，其基本思想是：任何一个规则或不规则的连续曲面均可以用n个规则曲面的叠加来拟合或逼近。该方法是从几何观点出发的一种曲面逼近法，解决根据数据点形成一个平差的数学曲面问题。该方法在大地水准面差距、重力异常、垂线偏差以及地壳变形等方面都取得了较好的拟合效果［8］。

在某一观测区域，每个观测点都可以同该区域中各个已知点分别建立函数关系，该函数称为核函数，它的图形是一个规则数学曲面，将这些规则数学曲面按一定比例叠加起来，就可拟合出任何不规则的曲面，且能达到较好的拟合效果［9］。多面函数在笛卡尔坐标系中的一般形式为

式中：βi为待定参数；F(x，y，xi，yi)为核函数；(x，y)为待求点坐标，其中心在 (xi，yi)处，为已知点坐标，核函数可以有多种表现形式，常用简单的核函数有以下几种：

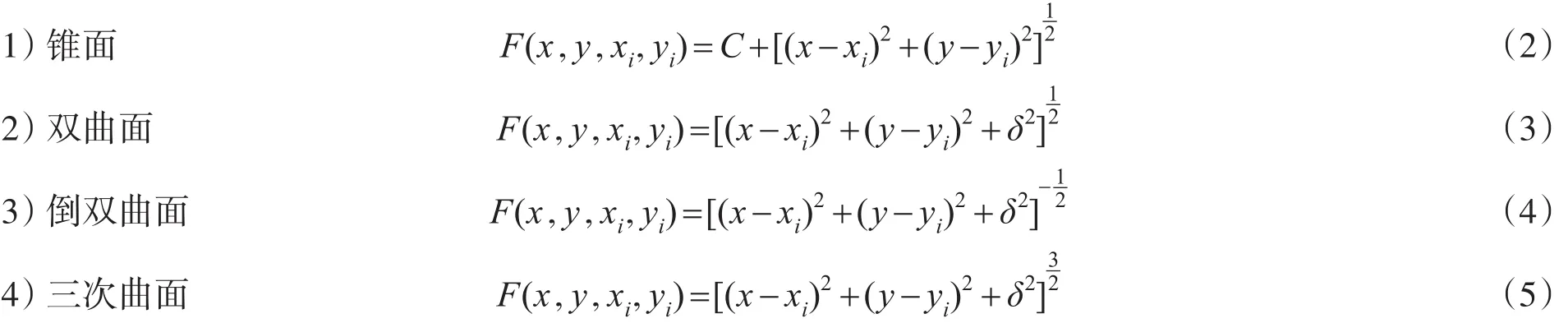
上述各式中，[(x-xi)2+(y-yi)2]为内插点到参考点之间的水平距离；C，δ是光滑系数，或称为平滑因子。

设已知海图深度基准面值有m个点，其m×1向量记为l，选取其中n个结点为j=1，2，3，…，n(n≤m)，β=(β1，β2，β3，…，βn)为n×1向量，当m＞n时，多面函数拟合法算法对应的误差方程式为V=Fβ-l，式中

在选择已知点时，最好选择测区中变化显著的点，这些点能很好描述该区域内各点的分布特征，一般位于最高、最低处以及坡度变化处。多面函数拟合法主要是确定核函数和平滑因子δ的选取，需要不断试验和改进［10］，以切合曲面局部的变化趋势，取得最佳的拟合效果。

2 拟合模型实例分析

为了探讨曲面拟合方法建立网格海图深度基准面模型的可行性，选择渤海湾作为实验区进行分析。实验区位于渤海西部，以大清河口至山东旧黄河口一线为界，面积约1.75 km2。深度基准采用国际海道测量组织推荐的最低天文潮面［11］，试验区共有1 369个深度基准数据点，周边地区158个数据点。该地区深度基准值范围在0.787～2.614m之间。分别采用4种核函数锥面、正双曲面、倒双曲面和三次曲面对模型进行计算，结果精度如表1～表4所示。

表1 锥面核函数拟合精度Tab.1 Fitting precision of cone surface kernel function

表2 正双曲面核函数拟合精度Tab.2 Fitting precision of right two curved-surface kernel function

表3 倒双曲面核函数拟合精度Tab.3 Fitting precision of reverse two curved-surface kernel function

表4 三次曲面核函数拟合精度Tab.4 Fitting precision of cubic surface kernel function

从表1～4的比较分析可知，在采用多面函数拟合深度基准面模型的过程中，核函数对平滑因子δ的依赖性不同，结果精度也有区别。其中，倒双曲面多面函数对平滑因子δ最敏感。在使用多面函数拟合法进行曲面拟合时，平滑因子δ的取值非常重要，一般规律是随着结点间平均距离的增加，δ值的选取也要增加，具体变化取值需要对已知数据点进行反复试算来确定。选取各个核函数取得最佳可调参数值状态进行比较，核函数为倒双曲面时拟合精度最佳，4种核函数的最佳拟合残差分布如图1所示。

通过对拟合计算过程的分析，可以得到如下结论：

1）不同的核函数对平滑因子δ显示出不同的依赖性，对拟合结果的精度也有相应的影响。其中倒双曲面多面函数对平滑因子δ最为敏感，参数选取稍有偏离就可能产生较大误差；而三次曲面多面函数对平滑因子δ的依赖性很弱，可以在比较大的范围内保持一定的拟合精度；对于正双曲面多面函数，当可调参数在一定范围内时，拟合精度随参数的变化而逐渐变化。在各自都取得最佳参数值时，倒双曲面多面函数的拟合精度高于其它3种。

2）使用多面函数拟合法进行曲面拟合时，平滑因子δ的取值非常重要，在选取时有一定的规律可循。一般若结点间的平均距离增加，则选取的δ值相应也要提高；反之亦然。δ可以取已知数据点间距平均值的倍数，具体要对已知数据点进行反复试算来确定。

采用拟合精度最好的倒双曲面多面函数拟合方法解算连续的渤海湾最低天文潮面模型如图2所示。

图1 多面函数拟合残差分布Fig.1 Residualdistribution of polyhedral function fitting

3 结语

图2 渤海湾连续最低天文潮面模型Fig.2 Depth datum model for BohaiBay

利用多面函数拟合法对渤海湾的最低天文潮面进行了拟合研究，分别采用锥面、正双曲面、倒双曲面和三次曲面为核函数对模型进行实例计算，拟合精度高，其中倒双曲面的综合精度最好，由此建立的连续最低天文潮面模型的残差值不超过15 cm，可以满足100m以浅海道测量30 cm的精度要求。需要注意的是，采用多面函数拟合深度基准面模型，节点位置的选择需要遵循点位分布均匀的原则，平滑因子也需要通过多次试算来择优而选，比较适合于已知采样点的单点精度比较高的情况。此外，与拟合结果精度类似的Kriging方法相比［13］，由于在计算核函数矩阵时计算量非常大，而对计算的速度能力要求更高。

插值法曲面拟合的方法很多，在陆地高程拟合中应用的方法也很多，后继研究中将选择其他拟合方法应用于深度基准面的连续化，以进行比对研究。

［1］暴景阳，刘雁春，晁定波，等.中国沿岸主要验潮站海图深度基准面的计算与分析［J］.武汉大学学报：信息科学版，2006，31（3）：224-228.

［2］ZHOU XINGHUA，SUN CUIYU，LENING，etal.The application of satellite altimetry in establishing regionalmean sea level［C］//The InternationalConference on Remote Sensing，Environmentand Transportation Engineering，Nanjing：IEEE，2010：3636-3639.

［3］GB12327—1998.海道测量规范［S］.北京：中国标准出版社，1999.

［4］ RUTH ADAMS.Seam less data and vertical datums reconciling chart datum w ith a global reference frame［J］.The Hydrographic Journal，2004（113）：9-14.

［5］许军.卫星测高技术在海洋动态垂直基准中的应用研究［D］.大连：海军大连舰艇学院，2005.

［6］ VAN NORDEN MAXIM F，LADNER RWADE，ARRORYOSUAREZ ELLIOT N.Developing a concept of operations for m ilitary surverys to IHO standardsw ithout shore-based stations［C］//Proceedings of the Canadian Hydrographic Conference and National SurveyorsConference2008，Toronto：Canadian Hydrographic Association，2008：243-254.

［7］WELLSDAVID，KLEUSBERG ALFRED，VANICEK PETR.A seam less vertical-reference surface for acquisition，managementand display（ecdis）of hydrographic data［R］.New Brunsw ick：Departmentof Geodesy and Geomatics Engineering University of New Brunsw ick，1996.

［8］于红波，刘惠明.GPS水准拟合的若干问题研究［J］.矿山测量，2009（1）：63-66，76.

［9］刘念，胡荣明.拟合推估在GPS高程解算中的应用［J］，测绘通报，2000（7）：29-31.

［10］南亲江，卜建阳.GPS高程曲面拟合算法的精度分析［J］.现代测绘，2008，31（4）：17-19.

［11］张力，孙新轩，刘雁春，等.最低天文潮面的精度研究［J］.海洋测绘，2009，29（4）：5-8.

［12］姬付全，经绯，刘志彬，等.利用3次样条插值确定室内压缩试验先期固结压力［J］.华东交通大学学报，2011，28（6）：96-100.

［13］陈艳华，孙翠羽，张化疑.基于Kriging方法建立连续深度基准面模型［C］//江苏省测绘学会2012学术年会，南京：江苏省测绘学会，2012：26-28.

［14］柯灏.海洋无缝垂直基准构建理论和方法研究［D］.武汉：武汉大学，2012.