对称振子阻抗特性分析

刘建厂 张秀强

（海司信息化部，北京100841）

引 言

天线在舰艇无线通信中起着重要作用，舰艇由于空间狭小，使用尺寸合适的线天线具有实际意义，研究对称振子是研究线天线的基础.天线参数有很多，输入阻抗是天线的重要参数，只有知道了天线的输入阻抗，才可以选取合适的馈电传输线与其连接［1-2］.

用解析方法严格求解天线的输入阻抗是很困难的，因为首先必须准确计算天线上的电流分布.在工程应用中，对于对称振子天线，经常使用一些近似方法，如坡印廷矢量法、等效传输线法和感应电动势法等，但这些近似方法比较适用于细振子天线，对于直径较大的振子，误差较大，此时，比较准确计算对称振子的输入阻抗只能使用数值计算方法，如矩量法、时域有限差分法和有限元法［3］等.矩量法在天线数值计算领域应用非常广泛，求解过程简单，步骤统一，一般情况下，可以给出在实验误差精度内的结果.

分析了前面提到的3种近似方法，重点是等效传输线法［3-6］.对解析方法——海伦积分法［1，5，7-8］求解对称振子输入阻抗的计算过程进行了研究，并与矩量法的数值计算结果进行了比较，最后计算了边靠边不等长平行对称振子的互阻抗.

1 对称振子的辐射阻抗

计算对称振子的输入阻抗，首先必须计算它的辐射阻抗，而计算辐射阻抗又必须确定对称振子的电流分布.如图1所示的细对称振子，振子半径为

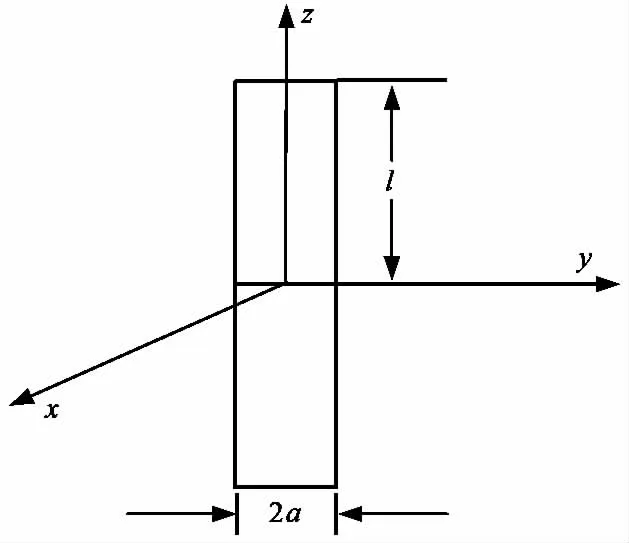
图1 对称振子示意图

a，一臂长为l，总长度为L＝2l，总是假定其上电流近似于正弦分布，可以写作

式中：Ⅰm为电流波腹点的复振幅；k＝2π／λ为自由空间相移常数.随着振子半径增大，电流分布与正弦分布出现偏差.对称振子辐射场的计算，可以参考相关教材，这里直接给出归算于波腹电流的辐射电阻Rr和辐射电抗

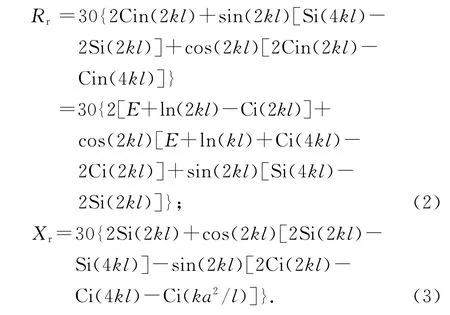
2 对称振子的输入阻抗

天线的阻抗特性包括辐射电阻和输入阻抗，如果不考虑天线的自身损耗，输入电阻等于归算于馈电点电流的辐射电阻［3］.

解析求解对称振子的输入阻抗是一个边值型问题，就是根据天线表面的边界条件和激励条件求解麦克斯韦方程组，常用的三种方法是长旋转椭球天线法、对顶双锥天线法和圆柱天线法［1，5］.长旋转椭球天线法尤其适用于分析粗振子天线；对顶双锥天线法适用于分析细振子天线，但这两种方法不能用来分析多根振子组成的天线；而圆柱天线法能用来分析多根振子组成的复杂天线［1］.

工程上计算对称振子的输入阻抗，一般使用前文所述的坡印廷矢量法、感应电动势法和等效传输线法等近似方法.

坡印廷矢量法是在天线的远场区对坡印廷矢量进行积分，将天线的辐射功率等效为一个电阻吸收的功率，这个等效电阻就是天线的辐射电阻，该方法只能得到辐射电阻，无法求得辐射电抗，得出的辐射电阻形式如式（2）所示.

感应电动势法是在天线表面对坡印廷矢量进行积分，因而可以得到辐射电抗，在振子较细的情况下，所得辐射电阻结果与式（2）相同，辐射电抗结果如式（3）所示，对称振子辐射电阻和辐射电抗随长度的变化曲线如图2所示.

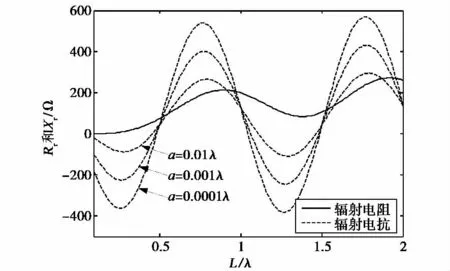
图2 对称振子辐射电阻和辐射电抗随长度变化曲线

结合坡印廷矢量法和感应电动势法得到的输入阻抗为［9］：

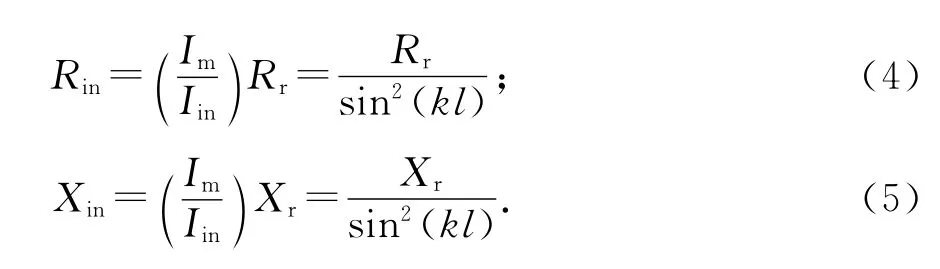
因为在工程上使用等效传输线法计算对称振子的输入阻抗比较简便，下面重点分析此方法.

2.1 等效传输线法

等效传输线法是将长度为2l、半径为a的对称振子天线看作距双线传输线终端l长的一段向相反方向张开90°形成的，因而可以等效为具有一定平均特性阻抗且终端开路的有耗传输线［2-3，5-6］.

如图1所示对称振子的平均特性阻抗

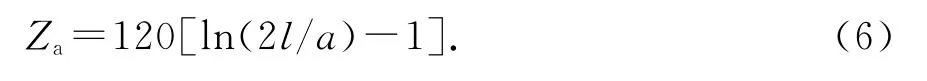
有耗传输线的传播常数

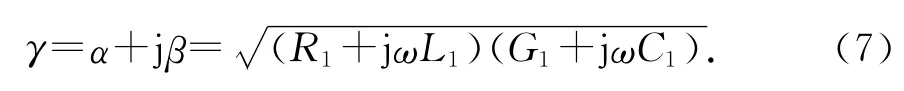
式中：α为衰减常数；β为相位常数；R1为单位长度电阻.忽略介质的漏电损耗和导线的热损耗，即G1＝0，且R1／ωL1≪1时，式（7）可表示为

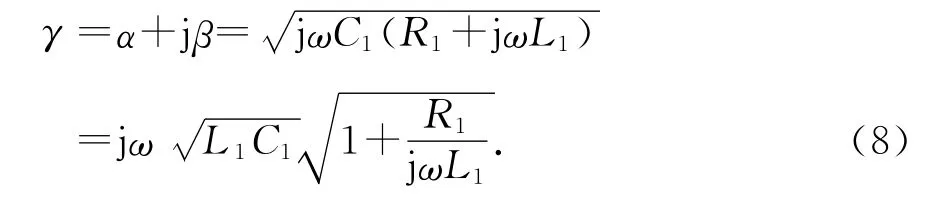
此时

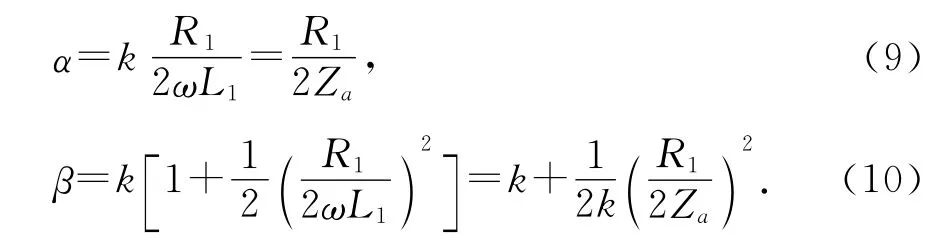
另外一种推导方式，求解方程组

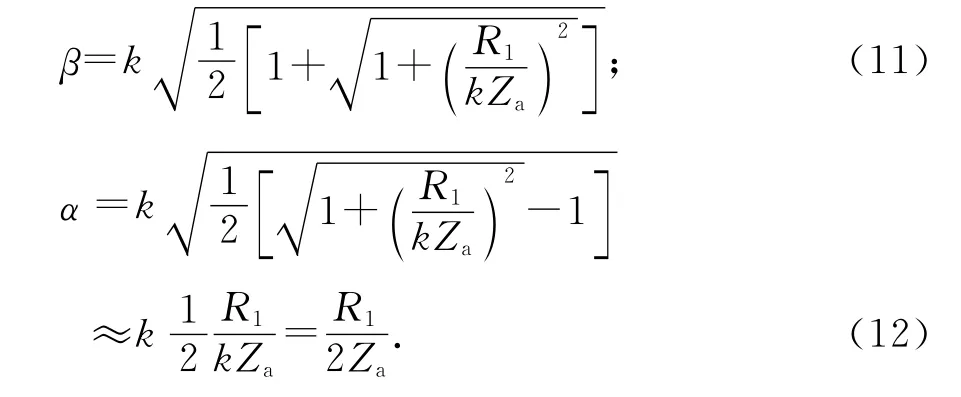
可以看出，两种方式所得的衰减常数是一致的，而相位常数的形式有所不同.实际上，式（11）通过两次级数展开，也能得出如式（10）形式的β值，此处采用式（11）形式的β值.

将对称振子的辐射功率等效为传输线分布电阻，即单位长度电阻R1的损耗功率，根据对称振子的损耗功率等于天线的辐射功率这一条件，即

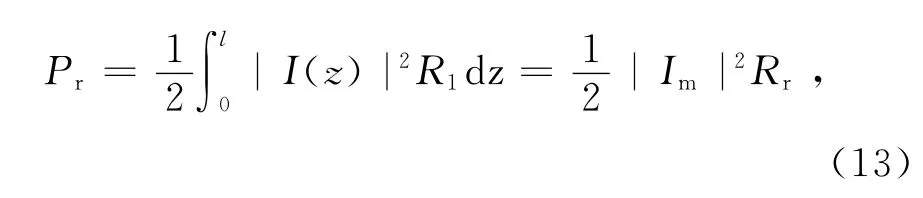
将式（1）带入式（13）可得

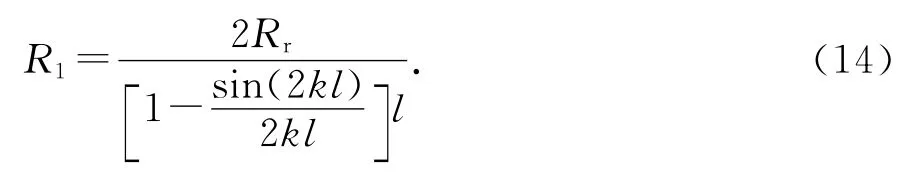
进一步得到衰减常数

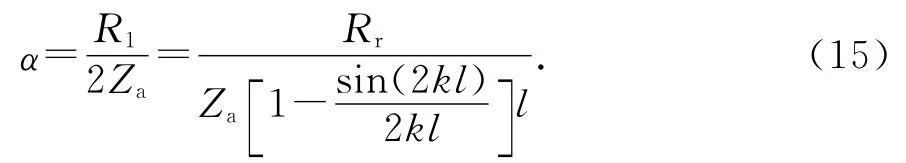
经过推导，得到输入阻抗为

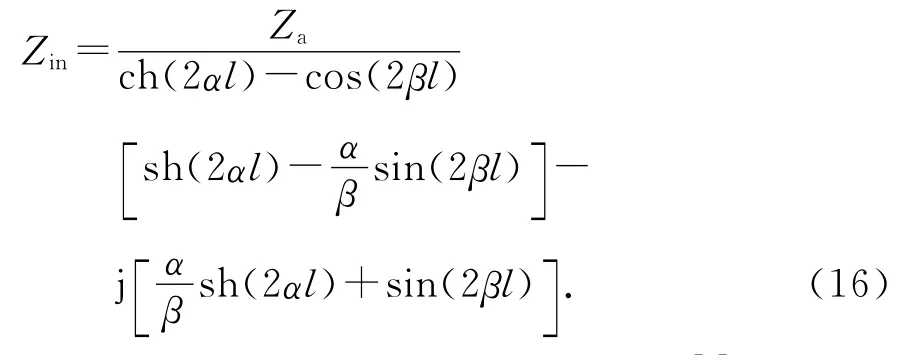
当0＜l／λ≤0.35和0.65≤l／λ≤0.85时［5］，式（16）可以化简为

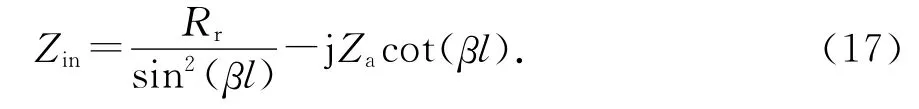
式（17）的实部与式（4）形式相同，只是相位常数不同.

2.1.1 分析比较

由式（11）可以看出：β＞k，这代表着天线上波长缩短了，产生这一现象的原因，一方面是由于对称振子的辐射引起了电流衰减，使得电流相速减小，线上相移常数大于自由空间相移常数；另一方面，对于有一定线径的对称振子，因为末端效应的存在，等效于振子长度增加了，也会造成波长缩短［2-6］.本文前面求得的相位常数实际上只考虑了第一个因素.波长缩短因子的计算非常复杂，一般靠实验数据得到［2-3，5］.

图3是根据式（16）计算所得的输入阻抗随振子长度的变化关系，对于半径a＝0.001λ的半波振子，通过计算得到的输入阻抗为（73-j2.7）Ω，可以看出输入阻抗是容性的，而实际上细半波振子的输入阻抗是感性的.这说明只考虑第一个因素，得到的结果误差比较大，有必要对第二个因素，即天线末端效应引起的误差进行修正，此处直接引用文献［6］的结果，对误差进行修正.

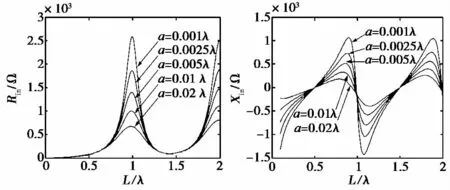
图3 对称振子输入阻抗随振子长度变化的关系

2.1.2 等效传输线法的修正

考虑到对称振子的末端效应，振子末端电流值实际并不为零，这相当于振子变长了，振子一臂增加的长度［6］为

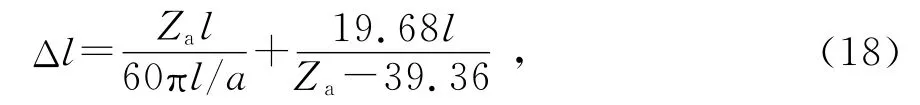
振子一臂长度变为

将式（16）重写如下

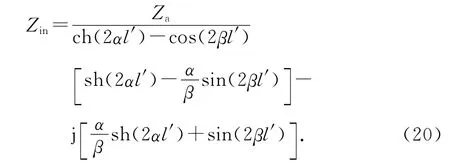
使用式（16）和式（20）分别对半径a＝0.01λ和a＝0.001λ的对称振子计算其输入阻抗，得到的数据如图4所示，图中实线是使用式（16）得到计算结果，虚线是使用式（20）得到的计算结果.可以看出，使用式（20）所得数据画出的曲线向左移动了，阻抗特性得到了改善，对于线径较大的半波振子，电抗值变为感性了.

作为比较，下面使用海伦积分法和矩量法来求解对称振子的输入阻抗.

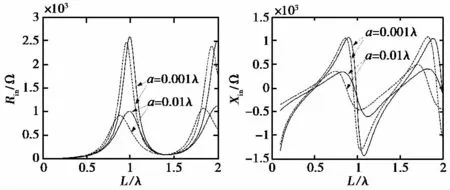
图4 修正前后对称振子输入阻抗与振子长度的关系

2.2 海伦积分法

对于图1所示的细对称振子，根据海伦积分方程［1，3，5，7-8］

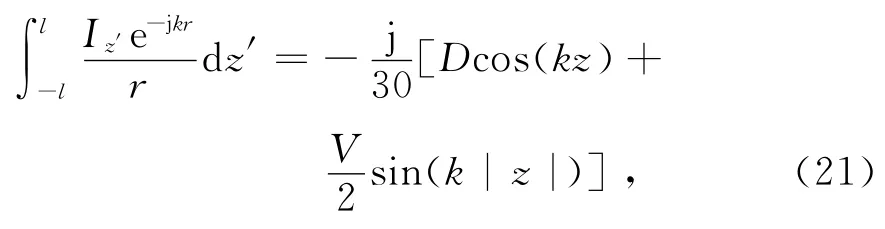
经过推导，可以得到电流分布的级数解为［1，5，7-8，10］

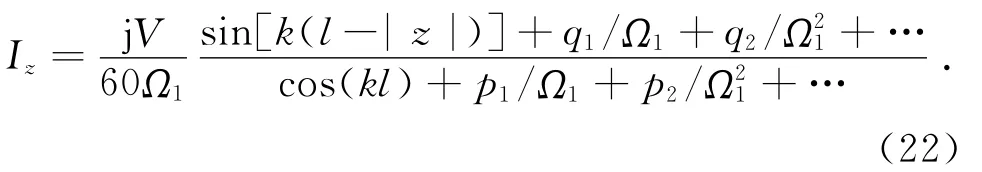
式中，V是输入端的电压.当z＝0时，得到输入阻抗二阶解为

式中：Ω1＝2ln（2l／a）；p1＝F1（l）；p2＝F2（l）；

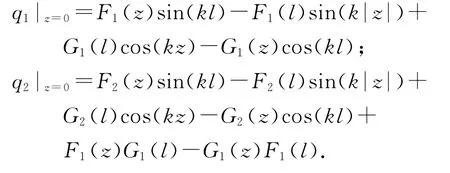
令

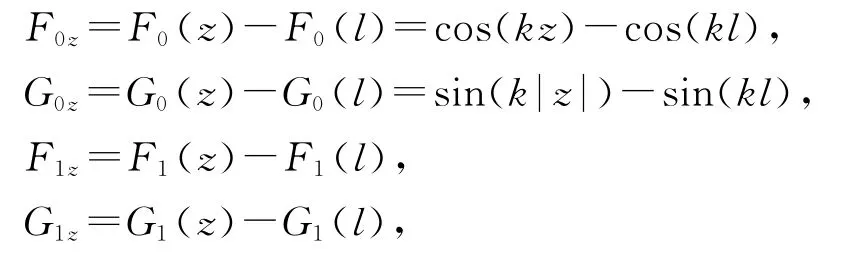
进而得到：

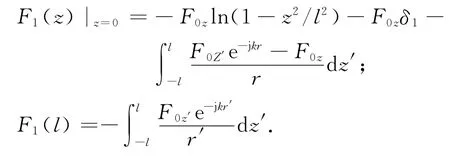
G1（z）和G1（l）形式与F1（z）和F1（l）分别相同.

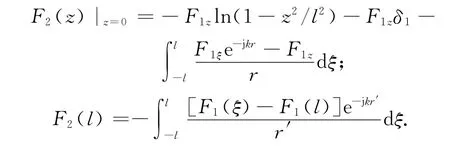
式中：

G2（z）和G2（l）形式与F2（z）和F2（l）分别相同.

在a≪l，ka≪1时，可以将r写作r＝｜z′-z｜，对于具有一定线径的天线，这样处理会使得电流分布在天线两端附近产生很大误差［7］，但在离开天线两个端点距离为天线半径的3～4倍后，误差就变得很小了.在这种情况下可以得出F1（l）、G1（l）、F1（z）和G1（z）的解析表达式［7，10］：

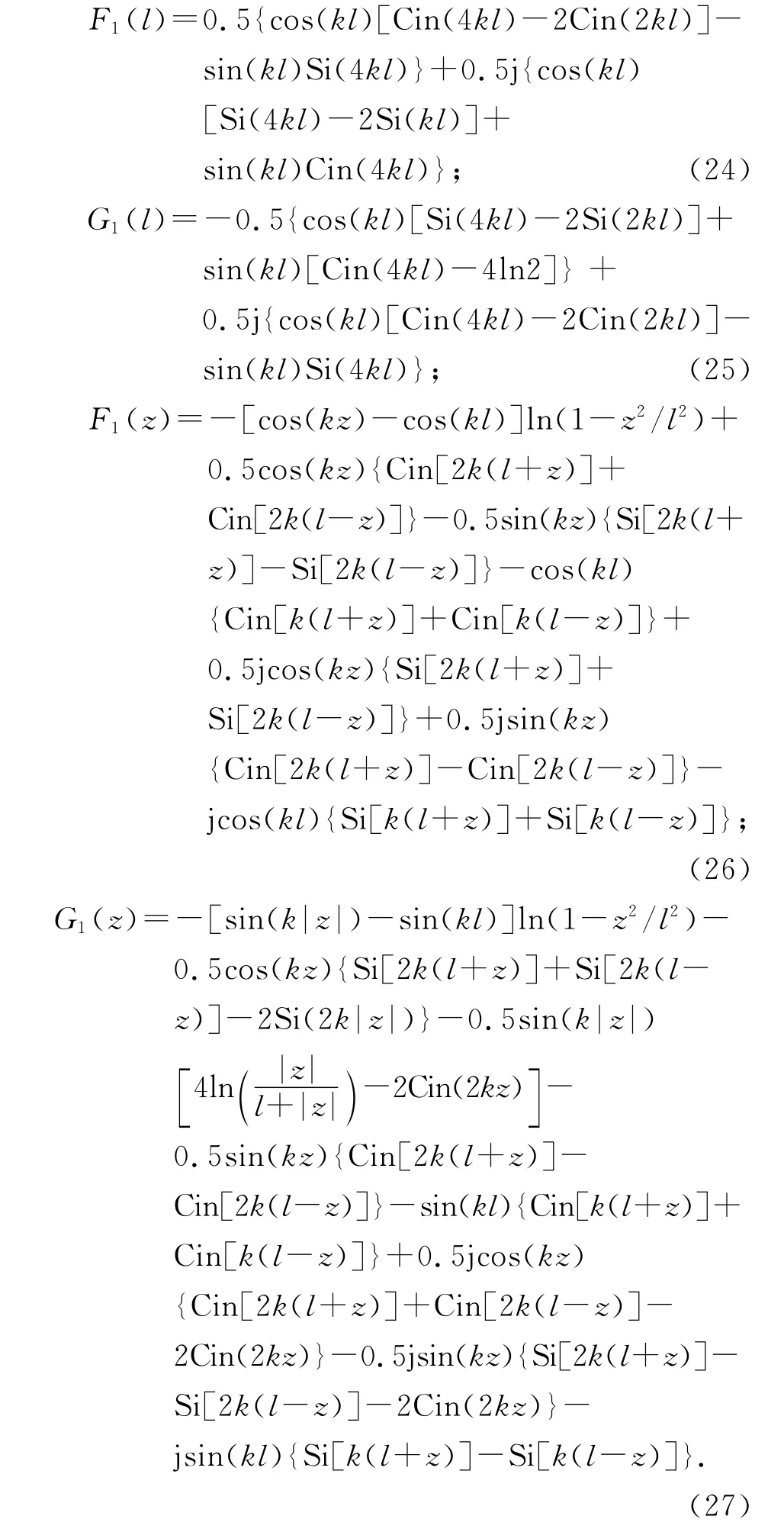
进一步得到

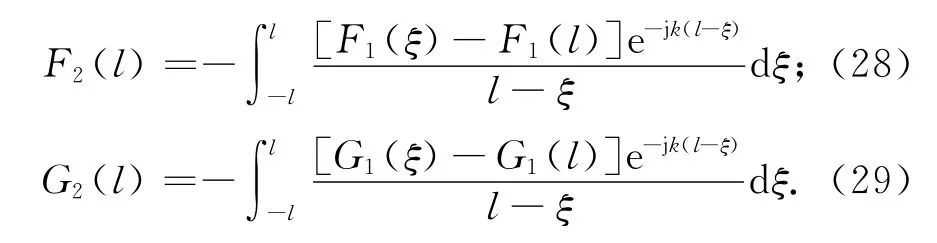
经过这样处理，可以得到输入阻抗一阶解析解，但在求解二阶解时，积分过程非常容易产生奇异值，使输入阻抗二阶解很不稳定，故文章中取r＝（a2＋（z-，采用原始积分法求解输入阻抗.

2.3 矩量法

在使用矩量法［3，5，11-14］过程中，选用反应积分方程，采用分段正弦基函数，应用伽略金法.

对如图1所示半径a＝0.001λ的对称振子使用三种方法计算输入阻抗所得结果如图5所示，图中实线是按照公式（20）计算所得结果；虚线是使用海伦积分法所得结果；星形线是矩量法的计算结果.可以看出，应用公式（20）所得结果与使用海伦积分法求得的二阶解差别不大，但与文献［15］中矩量法的计算结果还是存在一定差距，特别是在振子长度为0.8～1.3个波长时.相信随着阶数的增加，矩量法与海伦积分法求得数据的一致性应该很好.

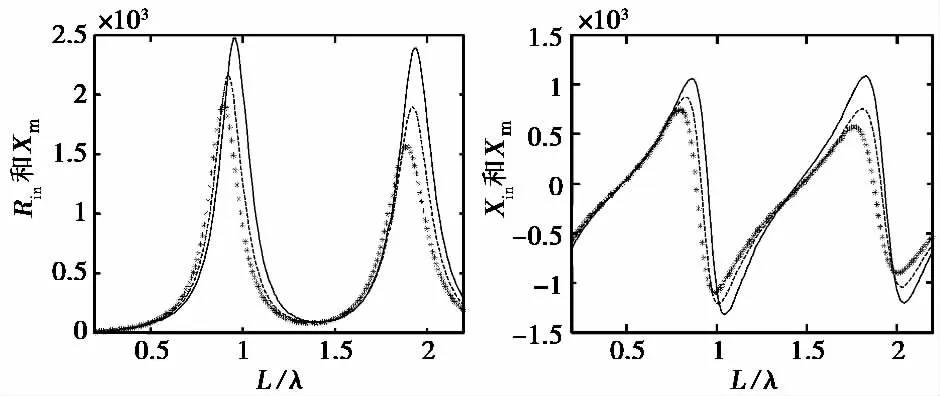
图5 三种方法计算的对称振子输入阻抗随长度变化关系

对于半波振子，公式（20）给出的输入阻抗值为（73.4＋j43.1）Ω，海伦积分法给出的输入阻抗二阶解为（79.4＋j40.3）Ω，矩量法给出的数值解为（83.9＋j43.3）Ω，由此可见，对于半径不是很大的半波长左右的对称振子，使用公式（20）可以得出比较准确的结果.

3 对称振子的互阻抗

文章只分析了如图6所示的两边靠边不等长平行对称振子的互阻抗.以振子2波腹电流为参考，振子1在振子2的输入端感应的开路电压［9，16］

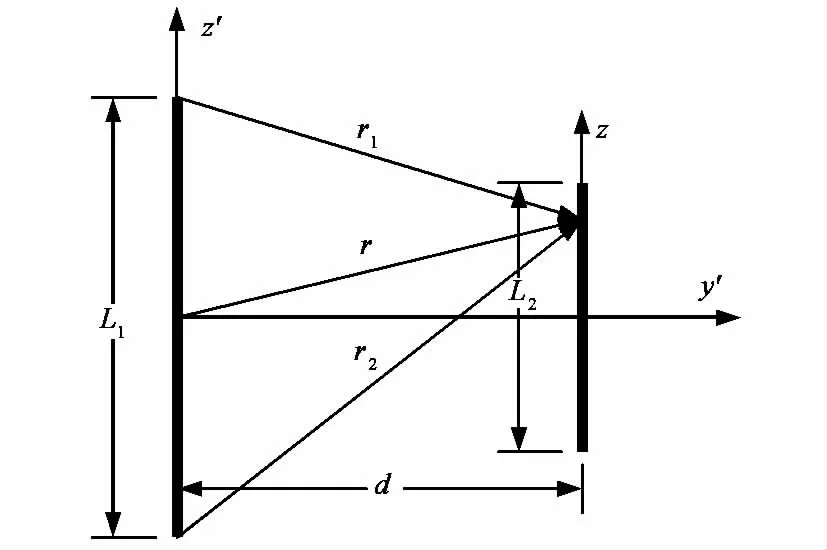
图6 边靠边不等长平行对称振子示意图

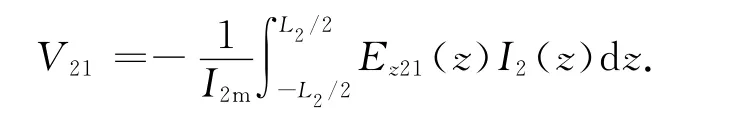
归算于振子1和振子2波腹电流的互阻抗为

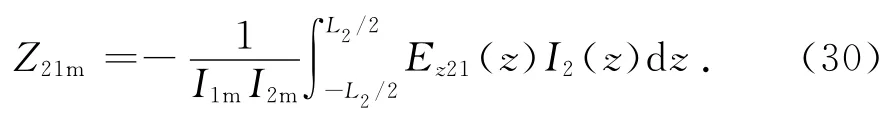
根据文献［9］的结果

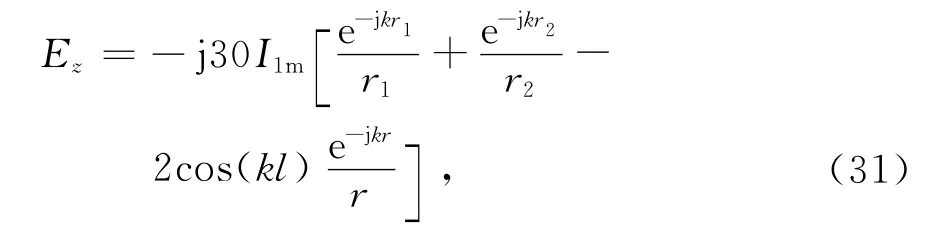
r1、r2和r分别是振子1的两个端点和中点到观察点的距离，对于如图6所示的两平行对称振子来说，可以看作是分别到振子2上某点的距离，即可以写作

将式（1）和（31）代入式（30），得到归算于振子1和振子2波腹电流的互阻抗

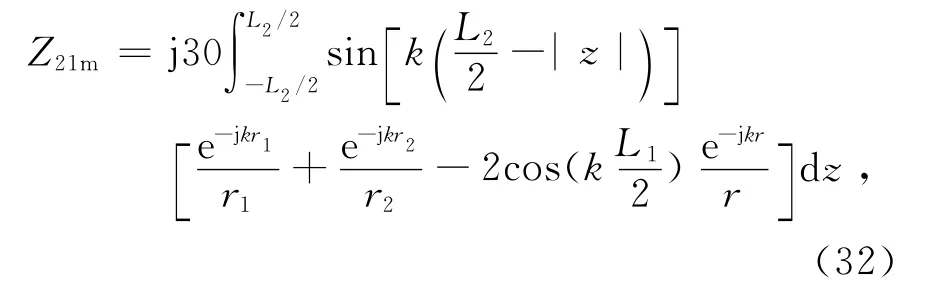
而归算于输入电流的互阻抗

L1＝0.5λ、L2＝0.45λ和L1＝0.6λ、L2＝0.4λ的两组边靠边不等长平行对称振子归于输入电流的互阻抗随间距变化的曲线如图7所示.

由图7可以看出：对称振子的互阻抗与振子半径无关，随着间距的增加，逐渐变得很小；且互阻抗对振子长度的变化不是很敏感，在对精度要求不是很高时，两半波长左右边靠边不等长平行对称振子的互阻抗可以用两边靠边平行半波振子的互阻抗来代替.

4 结 论

图7 边靠边不等长平行对称振子互阻抗随间距变化曲线

输入阻抗是一个重要的天线参数，振子粗细对输入阻抗的影响较大.文章详细分析了求解对称振子输入阻抗的各种理论和方法，包括近似方法（坡印廷矢量法、等效传输线法和感应电动势法）、解析方法（海伦积分法）和数值方法（矩量法），并着重对等效传输线法和海伦积分法进行了研究.

对等效传输线法的不足提出了实用的修正方法，分析了海伦积分法求解对称振子输入阻抗的过程，并推导了求解过程中各个重要参数.

通过将修正方法的计算结果与海伦积分法和矩量法的计算结果进行比较，证明了除去谐振点附近的点，对于一般对称振子，修正后的方法能得到比较准确的计算结果.下一步的研究重点是继续对复杂天线的输入阻抗求解理论和方法进行研究.

［1］任 朗.天线理论基础［M］.北京：人民邮电出版社，1980.

［2］宋 铮，张建华，黄 冶.天线与电波传播［M］.西安：西安电子科技大学出版社，2011.

［3］卢万铮.天线理论与技术［M］.西安：西安电子科技大学出版社，2004.

［4］褚国祯.中波天线输入阻抗计算机分析［J］.电波科学学报，2002，17（2）：197-203.CHU Guozhen.Analysis of input impedance of medium wave antenna with computer［J］.Chinese Journal of Radio Science，2002，17（2）：197-203.（in Chinese）

［5］钟顺时.天线理论与技术［M］.北京：电子工业出版社，2011.

［6］阮颖铮.用静电学和传输线理论计算圆柱形振子天线的输入阻抗—等效传输线法的修正［J］.通信学报，1981，1：96-106.RUAN Yingzheng.Calculation of the input impedances of cylindrical doublet antennae by the application of the static electricity and transmission line theoriesan amendment to the equivalent transmission line method［J］.J ournal of China Institute of Communications.1981，1：96-106.（in Chinese）

［7］KING R，HARRISON C W.The distribution of current along a symmetrical center-driven antenna［J］.Proc IRE，1943，31：548-567.

［8］MEI K K.On the integral equations of thin wire antennas［J］.IEEE Trans on AP，1965，13：374-378.

［9］康行健.天线原理与设计［M］.北京：北京理工大学出版社，1993.

［10］UDA S，MUSHIAKE Y.八木天线［M］.北京：人民邮电出版社，1961.

［11］HARRINGTON R F.计算电磁场的矩量法［M］.北京：国防工业出版社，1981.

［12］KRAUS J D，MARHEFKA R J.天线［M］.北京：电子工业出版社，2008.

［13］梁志伟，赵国伟，徐 杰，等.柱形等离子体天线辐射特性的矩量法分析［J］.电波科学学报，2008，23（4）：749-753.LIANG Zhiwei，ZHAO Guowei，XU Jie，et al.Analysis of plasma-column antenna using moment method.Chinese Journal of Radio Science.2008，23（4）：749-753.（in Chinese）

［14］NERI R.Input impedance of thin dipoles by moment me thod［J］.Electronics Letters，1979，15（14）：418-420.

［15］宋 铮，张建华，黄 冶.天线与电波传播学习指导［M］.2版，西安：西安电子科技大学出版社，2011.

［16］COX C R.Matual impedance between vertical antennas of unequal heights［J］.Proc IRE，1947，35：1367-1370.