光学遥感器进光口模拟外热流的均匀性分析

徐冰 马龙 王昭鑫

(北京空间机电研究所，北京100076)

1 引言

高真空、空间外热流和冷黑背景是太空中最主要的空间环境因素[1]。当卫星在轨运行时，所受到的空间外热流主要包括3部分能量: 太阳的直射能、地球及其大气反射的太阳能和地球的辐射能。遥感卫星相机对工作温度水平要求较高，为保证相机的成像品质和稳定性，相机透镜径向及轴向温度梯度应尽量小。空间外热流是影响其温度均匀性的主要因素。

为了验证相机热控方案的合理性以及相机在太空环境能否正常工作，必须对相机进行充分的空间热环境模拟试验。遮光罩进光口处投入的是均匀的太阳、地球红外以及反照热流，在空间热环境模拟试验中广泛地采用红外笼模拟遮光罩进光口的投入热流。红外笼投射热流的大小以及均匀性将影响模拟外热流的真实性和可靠性，从而对验证相机热控设计合理性产生至关重要的影响。

相机在试验中需要进行成像工作，热流均匀性非常好的平板式红外笼会遮挡相机的光路。若相机成像过程中移开红外笼，相机遮光罩进光口处的热流将发生突变，为了避免红外笼对相机成像的影响，试验中多使用筒式结构的红外笼。相机遮光罩的进光口多是圆形开口，本文针对适用于圆形进光口的筒式红外笼，通过合理的建模并运用ANSYS仿真计算，深入分析了红外笼结构对遮光罩进光口模拟外热流的均匀性影响。

2 红外笼结构设计

相机在轨运行时，轨道面、太阳与地球之间的相对位置不断变化，导致辐照的角系数也不断变化，而且轨道日照区和阴影区的热环境有很大差别; 不同的相机所在的轨道也差别很大[2]。遮光罩进光口的外热流密度一般在100～500W/m2之间。在空间热环境模拟试验中，模拟遮光罩进光口外热流入射面的外热流是一项重要的试验指标。根据相机热控设计以及结构特点，通常使用筒式红外加热笼模拟遮光罩进光口外热流入射面的外热流，在100～500W/m2的范围内连续可调，并且入射面的热流不均匀度小于5%。为了满足不均匀度以及试验安装要求，对试验所使用的红外笼结构进行优化是必不可少的工作。

文中采用入射面不同点的热流波动度的均方根值来分析不均匀度，其中波动度η的定义为:

式中 Δqavg为各检测点热流密度的均方根值;qavg为热流密度算术平均值。

根据以上公式计算的η值表示热流在平均值上下的波动范围，因此，根据以上公式得出的η值应小于2.5%才能满足热流不均匀度小于5%的要求。下文都采用波动度来进行热流均匀性分析。

本文分析了适用于圆形进光口的筒式红外笼的结构与进光口模拟外热流均匀性之间的关系。其最小口径必须不小于遮光罩的进光口径，可分为圆柱形和锥形两种:

1)圆柱形红外笼安装方式如图1(a)所示，其结构简单，文中定义其半径为RY，长度为LY;

2)锥形红外笼的上下开口半径大小不同，文中定义半径较小的开口面为顶面，反之为底面; 其顶面半径为RZ，长度为LZ，锥角为α。为了保证光路以及遮光罩连接处外热流入射面的均匀性，底面与遮光罩端面进行连接，如图1(b)。

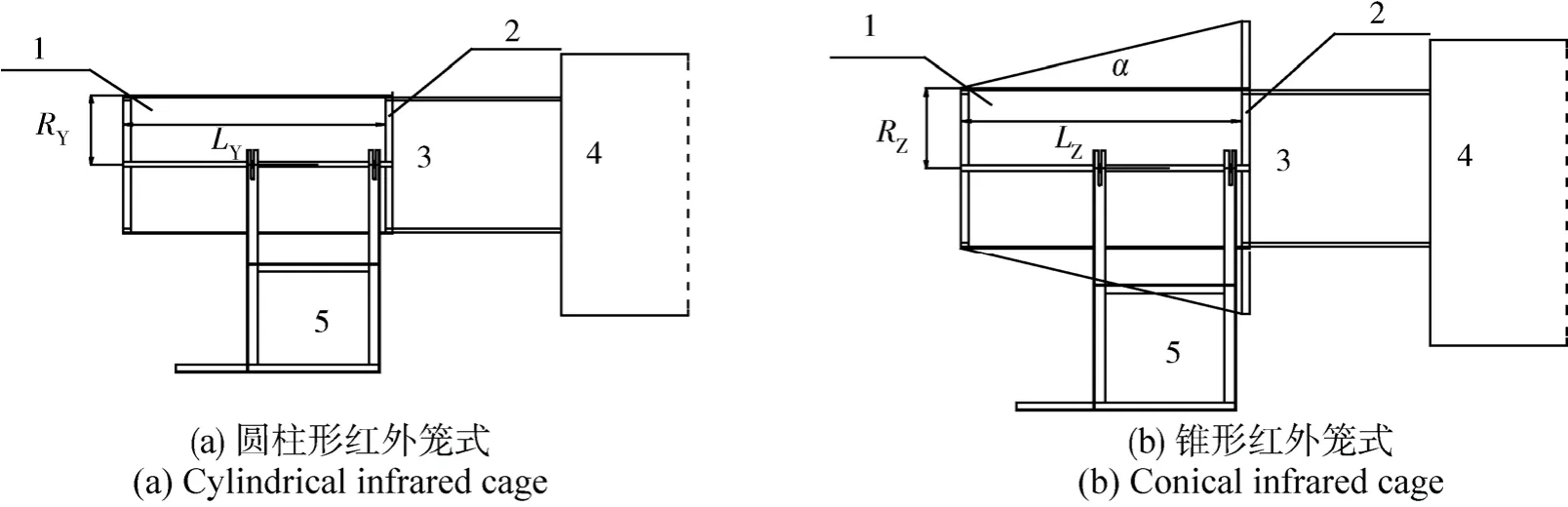
图1 加热笼与遮光罩位置结构Fig.1 Location map of the heating cage and hood

3 模拟仿真计算

本文利用ANSYS对红外笼所投入外热流进行模拟计算。ANSYS能够自行建立和读取三维CAD模型，并能够提供为计算模型全面的数学模型、网格划分处理以及高精度的求解计算。

3.1 模型及边界条

筒状红外加热笼的辐射带条即可以呈直线状沿外热流入射面边缘轴向分布，也可以呈圆环状轴向分布; 但是圆环状带条加工难度大，若自身结构不均匀，将导致模拟外热流的均匀性受到影响。因此，试验中都采用直线状的辐射带条。遮光罩进光口外热流入射面的热流密度均匀性的主要影响因素包括: 红外笼加热带的密度、加热带本身的温度均匀性以及红外笼的自身结构。当加热带条越密，且足够长时，进光口入射面的热流就越均匀; 但试验过程中需要通过热沉冷背景调整热流值的大小，通常加热带的覆盖率在30%～50%之间。

本文建模分析时假定加热带宽度和厚度分别为10mm和0.2mm，红外笼带条覆盖率为40%。由于红外笼、遮光罩、液氮热层之间的换热过程是三方辐射换热互相耦合的结果，因此在建模分析过程作了一定的简化处理:

1)环境是温度为100K、吸收率为1的冷黑空间;

2)加热带材料的导热系数是 40W/(K·m)(不随温度改变)，红外笼总加热功率按加热带的面积均匀分布，并忽略了红外笼边框的影响;

3)加热带内侧表面是发射率为0.92的刷黑表面，而外侧表面作为绝热面。

图2 红外笼分析模型Fig.2 Model of infrared heating cage

分析计算模型见图2，模型中每条加热带按照长度划分节点，每个节点的加热带长度0.05m; 以遮光罩进光口的外热流入射面为分析对象，若在该平面上均布若干个微圆面，每个微圆面对红外笼一侧是发射率为 1的黑体表面，面对遮光罩一侧的发射率为 0; 对加热带上施加适当功率实现外热流的模拟，功率载荷的改变会引起模拟热流的变化。

当微圆面处于热平衡状态时，热流控制方程为:

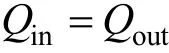
其中输入热流Qin为红外笼投入的辐射热流，输出热流为:

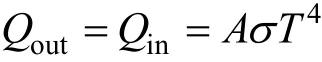
式中A为有效辐射面积;σ为斯忒藩-玻耳兹曼常数;T为热力学温度。

当微圆面的温度已知时，即可计算得到该微圆面的输入辐射热流，从而可得到红外笼对遮光罩进光口的外热流入射面的热流分布情况。入射面中各微圆面的温差越小，其热流密度就均匀。微圆面上的热量来源于红外笼加热带的辐射面，属于多个平面之间的辐射传热。多个辐射面之间传热用 AUX12辐射矩阵单元[4]建立辐射模型进行计算，其基本控制方程如下:

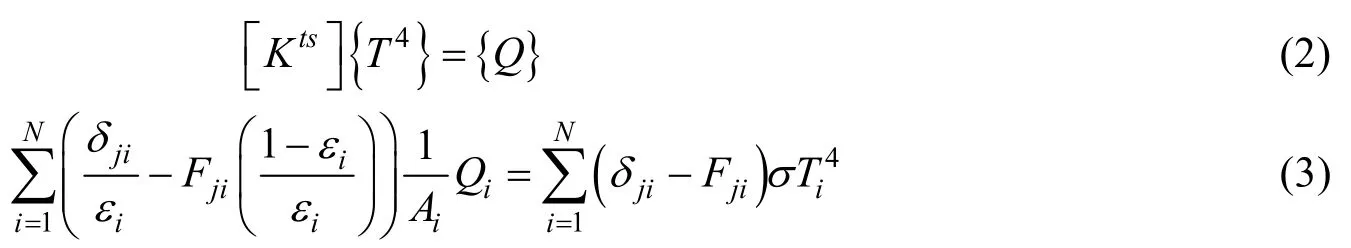
其中 [Kts]为多平面辐射效果;δ为科氏符号;Q为表面热流密度;ε为辐射率;F为角系数。

分析计算时取420 W/m2作为进光口外热流入射面的模拟目标值，在模型计算中存在一定简化和假设条件，并要求计算结果对 100～500 W/m2的目标值仍然有效。根据计算经验，筒式红外笼的模拟外热流的波动度小于2.5%作为合格判断标准更为合适。

3.2 圆柱形红外笼模拟计算分析

3.2.1 计算结果

当圆柱形红外笼的带条覆盖率和半径一定时，外热流入射面的热流均匀性只受到长度影响。将外热流入射面分为若干个微圆面进行热分析，获得其整体的温度场分布。本节分别对LY=0.4～1.6m、RY=0.3m的13种圆柱形红外笼，通过改变加热带的功率载荷并以420 W/m2作为目标热流值进行分析计算。

由于圆柱形红外笼带条相对外热流入射面的圆心成对称均匀分布，因此，入射面上与圆心距离相同的各微圆面温度差别不大，等温区域以同心圆形式分布。在外热流入射面上取与X轴重合的半径，该半径上微圆面的温度映射曲线就能反映出整体的温度分布情况; 径向温度曲线越平稳，则温度越均匀，外热流均匀性越好。图3～5为LY分别等于0.5m和0.9m时的温度场分布和径向温度曲线，遮光罩进光口外热流入射面的热流密度均匀性与红外笼长度密切相关。

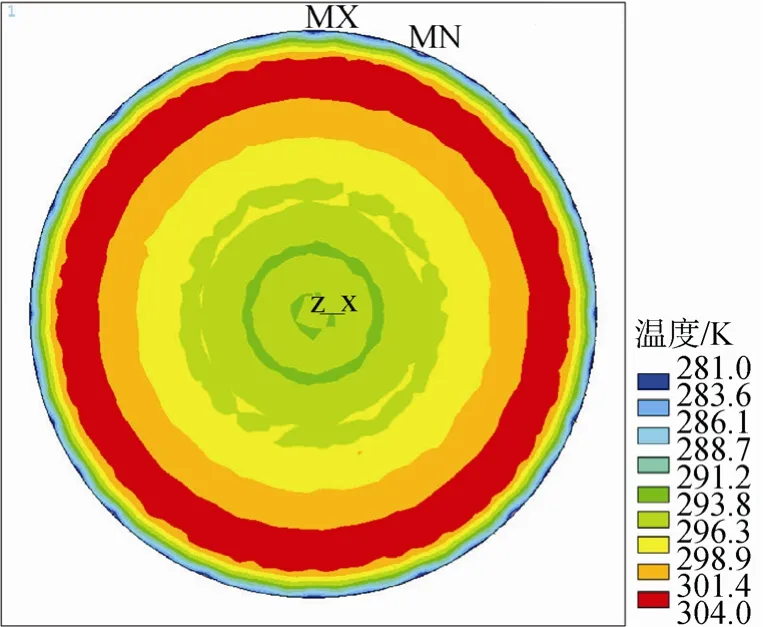
图3 LY=0.5m时外热流入射面温度场分布Fig.3 Temperature distribution of the external heat flux incident surface at LY=0.5m

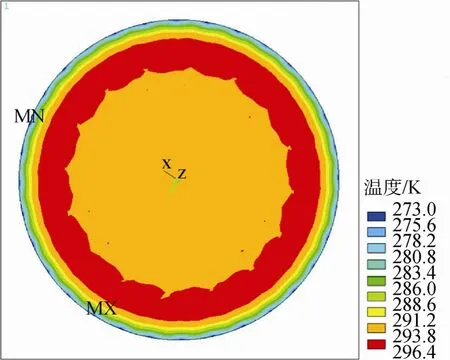
图4 LY=0.9m时外热流入射面温度场分布Fig.4 Temperature distribution of the external heat flux incident surface at LY=0.9m

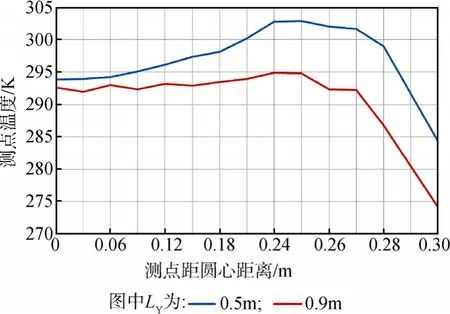
图5 LY=0.5m，0.9m时外热流入射面的径向温度曲线Fig.5 Temperature distribution of the external heat flux incident surface at LY=0.5m, 0.9m

3.2.2 结果分析

从整体的计算结果来看: 圆柱形红外笼长度越长，温度分布越均匀。以所取半径为路径，从圆心沿半径方向依次取距圆心距离为0.03、0.06、0.09、0.12、0.15、0.18、0.21、0.24、0.25、0.26、0.27、0.28、0.29以及0.30m的14个参考点与圆心的热流值作为参考进行详细计算分析。长度不同的圆柱形红外笼，各参考点的热流密度波动度情况参见图 6。从计算结果可以得知，离圆心越近的区域，外热流均匀性越好; 随着红外笼长度的增加，波动度小于2.5%的区域越大，中心区域的均匀性也越好。因此，增加圆柱形红外笼长度是提高进光口外热流均匀性的有效手段。

从图6的结果来看，若以2.5%的波动度为判定标准，对于RY=0.3m、带条覆盖率在40%以上的圆柱形红外笼，当LY≥1.1m时，能够提供有效的均匀外热流入射面的半径为0.28m; 即使再增加红外笼的长度，也难以扩大满足波动度小于2.5%的外热流入射面区域。因此，对于这种规格的圆柱形红外笼只适用于进光口半径不大于0.28m的遮光罩。

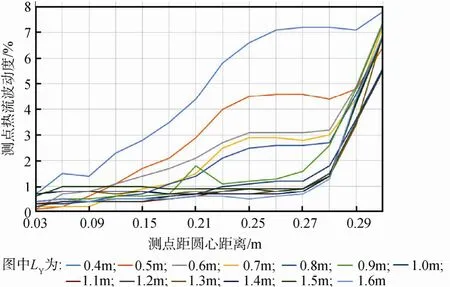
图6 圆柱形红外笼的外热流入射面参考点热流波动度Fig. 6 Heat uniformity of the reference points on the external heat flux incident surface of cylindrical infrared cage

3.3 锥形红外笼模拟计算结果

3.3.1 计算结果

锥形红外笼的结构比圆柱形要复杂，结构的变化对外热流均匀性影响较大，当带条覆盖率和顶面半径一定时，除了红外笼的整体长度以外，还受锥角大小的影响。本节分别对LZ=0.6～1.0m、RZ=0.3m以及α大小不同的15种规格的锥形红外笼，以420 W/m2作为目标热流值进行仿真计算。与上节圆柱形红外笼的计算处理方法相同，其整体的温度场分布与圆柱形相似，入射面上的等温区域以同心圆形式分布，均匀性要更好。例如: 当LZ=0.9m，α=10°时的温度场分布和径向温度曲线如图7和图8所示。

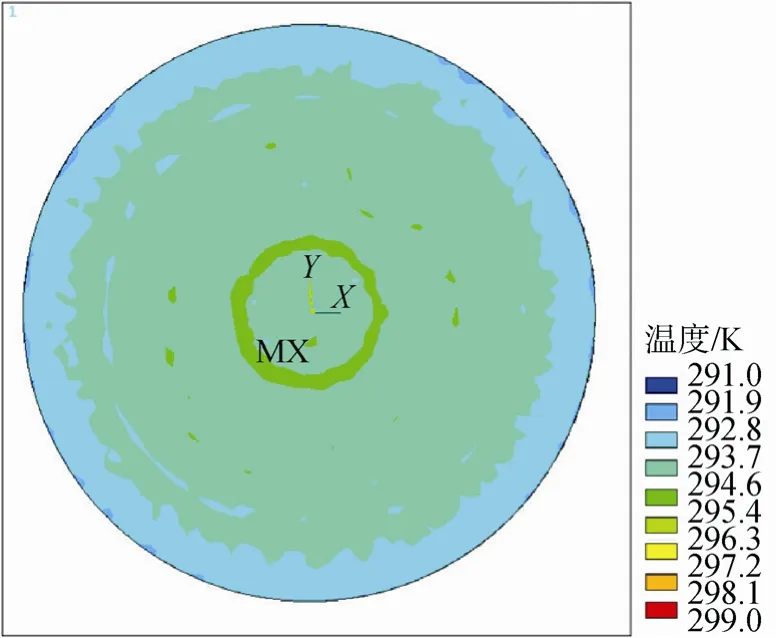
图7 LZ=0.9m、α=10°时外热流入射面温度场分布Fig.7 Temperature distribution of the external heat flux incident surface at LZ=0.9m、α=10°

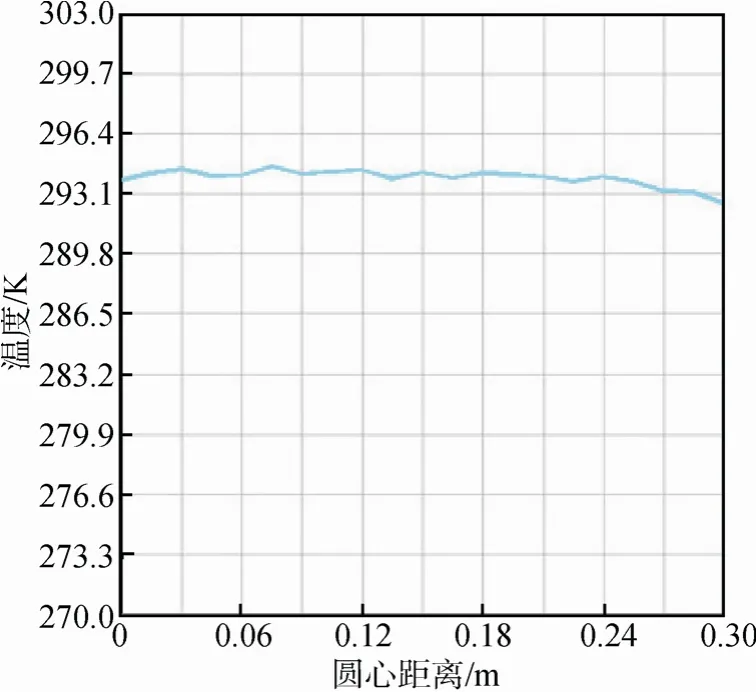
图8 LZ=0.9m、α=10°时外热流入射面的径向温度曲线Fig.8 Temperature distribution of the external heat flux incident surface at LZ=0.9m、α=10°

3.3.2 结果分析

按圆柱形红外笼的参考点分析方法，取同样位置的14个参考点进行计算分析。结构不同的锥形红外笼，各参考点的热流密度波动度关系如图9所示。其外热流均匀性和圆柱形红外笼的分布规律类似，离圆心越近的区域，外热流均匀性越好; 随着锥角和长度的变化，外热流入射面的热流均匀性也随之改变。总体来说，均匀性随着长度和锥角的增加而提高。

若以2.5%的波动度为判定标准，对于顶面半径RZ=0.3m、带条覆盖率在40%、LZ≥0.7m、5°≤α≤15°的锥形红外笼，与同等长度圆柱形红外笼相比有着更好的均匀性，能够为进光口半径在 0.3m以下的遮光罩提供非常均匀的外热流。

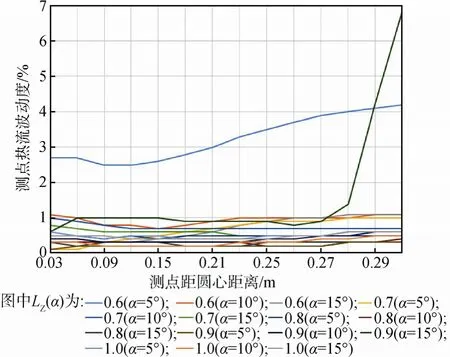
图9 锥形红外笼的外热流入射面参考点热流波动度Fig.9 Heat uniformity of the reference points on the external heat flux incident surface of conical infrared cage

4 红外笼结构与均匀性分析

从上节的计算结果发现: 满足均匀性要求的入射区域面积随红外笼结构的变化而变化，距离红外笼边界越近的地方，热流均匀性越差。由于外热流入射面仅获得红外笼的辐射热流，与加热带条的传热属于多个面之间的辐射传热。根据两平面之间的辐射互相作用法则和斯蒂芬-波尔茨曼法则[7]，平面i与平面j之间的传热公式为:

式中F为角系数;Qi–j为两个平面间的辐射传热量;A为有效辐射面积;ε为发射率。

那么当辐射面积和发射率一定时，热流密度仅与角系数相关。本次计算中，各微圆面的大小和带条面积是固定的，最终计算结果为热流密度，所以参考微圆面所获得的热流密度只与各加热带条辐射面的角系数相关。外热流入射面上各参考微圆面与带条辐射面的相对位置是决定角系数的唯一变量。筒式结构形红外笼的结构对称，且带条均匀排布，在加热带条宽度一定的情况下，红外笼的结构比例成为影响角系数的唯一因素。如果将遮光罩进光口的外热流入射面的半径定义为rY，那么红外笼的长度和半径、外热流入射面的半径RY以及外热流波动度之间存在一定的比例关系。根据RY=0.3m、LY=0.4～1.6m的圆柱形红外笼与遮光罩进光口的外热流入射面中 14个参考点的计算结果，列举出了半径与长度的比值在3/4～3/16之间的圆柱形红外笼，其结构与进光口外热流入射面半径以及热流波动度之间的关系，具体比例分布关系如图10所示。同样的方法，推导出了长度与顶面半径的比值在3/6～3/10之间的锥形红外笼，其结构与进光口外热流入射面半径以及热流波动度之间的比例关系(如图11)。

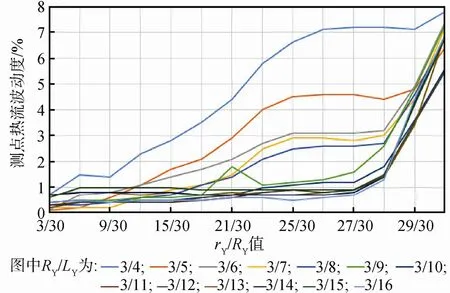
图10 圆柱形红外笼结构与进光口外热流入射面半径以及热流波动度的关系Fig.10 The relationship between structure of infrared cylindrical cage, radius of external heat flux incident surface and heat uniformity

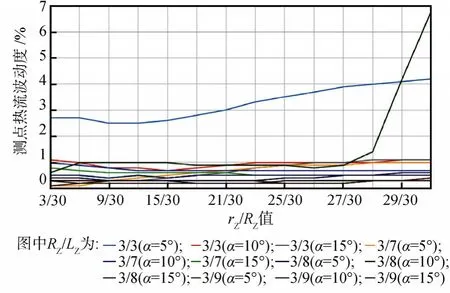
图11 锥形红外笼结构与进光口外热流入射面半径以及热流波动度的关系Fig.11 The relationship between structure of conical infrared cage, radius of external heat flux incident surface and heat uniformity

5 结束语

本文通过仿真计算，分析了筒式红外笼结构对其进光口热流均匀性的影响，并找到了外热流入射面半径与筒式红外笼结构之间的比例关系，为相机的空间热环境模拟试验的红外笼设计提供了理论依据。

文中所涉及到的两种红外笼各有特点，需要根据试验要求和环境选择更为合适的结构。当试验要求提供的均匀外热流入射面面积一定时，就能方便设计出满足试验要求的红外笼结构，但需要注意如下几点:

1)圆柱形红外笼相对于锥形筒状红外笼来说，结构简单、易于加工，而且结构高度对称、带条覆盖率更为均匀;

2)锥形红外笼能够提供更为均匀的外热流入射面，并能够有效的节省试验空间，但是结构复杂、加工难度大，难以做到均匀对称，从而严重影响其外热流入射面的热流均匀性;

3)红外笼口径尺寸应与遮光罩进光口尺寸保持合理比值，不宜差别过大，红外笼与遮光罩进光口之间的间隙需要填充防辐材料，减少漏热影响。

References)

[1] 闵桂荣, 郭舜. 航天器热控制[M]. 北京: 科学出版社, 1998.MING Guirong, GUO Shun. Spacecraft Thermal Control[M]. Beijing: Science Press, 1998.(in Chinese)

[2] 闵桂荣, 张正纲, 何知朱. 卫星热控制技术[M]. 北京: 中国宇航出版社, 2009.MING Guirong, ZHANG Zhenggang, HE Zhizhu. Satelite Thermal Control Technology[M]. Beijing: China Aerospace Press,2009. (in Chinese)

[3] 孙玉玮, 杨晓宁. 红外加热笼边缘效应对卫星表面热流均匀性的影响研究[J]. 航天器环境工程, 2006, 23(4): 222–226.SUN Yuwei, YANG Xiaoning. Simulation Study for the Optimal Design of Conical Infrared Heating Cage[M]. Spacecraft Environment Engineering, 2006, 23(4): 222–226. (in Chinese)

[4] 王泽鹏, 张秀辉. ANSYS12.0热力学有限元分析[M]. 北京: 机械工业出版社, 2010.WANG Zepeng, ZHANG Xiuhui. ANSYS12.0 Thermodynamics of Finite Element Analysis[M]. Beijing: China Machine Press,2010. (in Chinese)

[5] 何受全, 黄本成, 何传大, 等. 卫星环境工程和模拟试验[M]. 北京: 中国宇航出版社, 2009.HE Shouquan, HUANG Bencheng, HE Chuanda, et al. Satellite Enviroment Engineering and Simulation Testing[M]. Beijing:China Aerospace Press, 2009. (in Chinese)

[6] ANSYS Inc. ANSYS Modeling and Meshing Guide[M]. Twelfth Edition. Canonsburg: SAS IP Inc, 2001.

[7] 杨世铭, 陶文铨. 传热学(第四版)[M]. 北京:高等教育出版社, 2006.YANG Shiming, TAO Wenquan. Heat Transfer[M]. Beijing: Higher Education Press, 2006. (in Chinese)

[8] 赵立新, 邵英. 空间望远镜的热设计和热光学分析综述[J]. 航天返回与遥感, 2001, 22(2): 13–19.ZHAO Lixin, SHAO Ying. Summary of Thermal Control and Thermal-optical Analysis for Space Optical System[J]. Spacecraft Recovery & Remote Sensing, 2001, 22(2): 13–19. (in Chinese)