火星探测中进入弹道与大气模型重建

王文强

(北京空间机电研究所，北京 100094)

1 引言

作为深空探测的主要内容之一，火星探测是一个国家航天科技实力的集中体现[1]。从美国和俄罗斯/苏联几十年的火星探测任务中可以发现，实现软着陆探测是获取火星相关资料的主要的探测方式和目标。而要开展火星表面软着陆探测，首先需要获取任务设计所必须的大气密度、风速随高度的变化曲线，建立初步的火星表面大气模型[2]。

目前，我国对火星大气的了解几乎完全基于国外公开发表的相关文献资料。考虑到文献来源的可靠性以及火星大气参数的不稳定性，通过火星探测获取数据建立火星大气模型是我国开展进一步火星探测的必要步骤。

另一方面，由于火星着陆任务中探测器飞行时间较长，同时再考虑到火星大气的不确定性等因素，实际着陆弹道将严重偏离标准弹道。因此记录着陆过程的气动参数并重建进入弹道是对火星探测器进行任务分析和性能评估的重要措施，同时也为后续探测器任务设计提供参考依据。

本文以“火星科学实验室”(Mars Science Laboratory, MSL)为研究对象，讨论了火星探测中大气模型以及进入弹道的重建方法，为我国未来将要开展的火星探测以及建立火星大气模型提供依据。

2 MSL数据获取系统介绍

为了测量进入舱在进入火星大气时的大气环境和热环境，MSL进入舱安装了1套火星进入减速着陆仪器系统(Mars Entry, Descent, and Landing Instrumentation, MEDLI)[3-4]，如图1所示，图中不同颜色代表预估的防热罩表面压力大小，红色处压力最大，绿色最小。

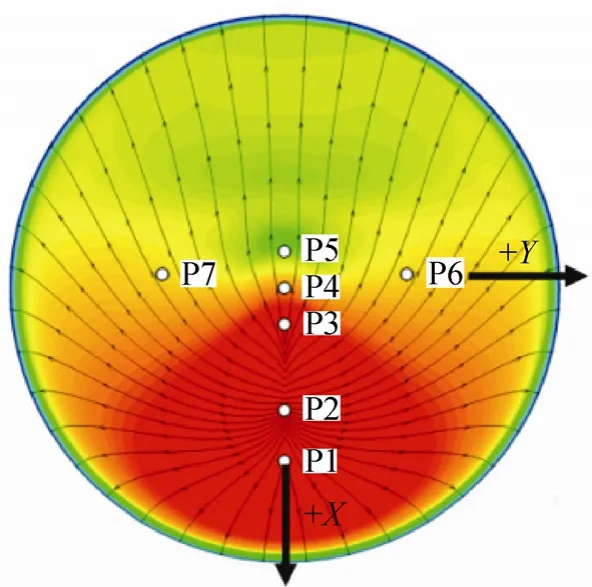
图1 MEADS测量单元安装位置Fig.1 MEADS port geometry

MEDLI由安装在MSL防热罩上的1组传感器组成，依据传感器类型和主要功能可以分为3个部分，分别为传感器集成插头(Mars Integrated Sensor Plug, MISP)，数据采集系统(Mars Entry Atmospheric Data System, MEADS)以及传感器电子支持设备 (Sensor Support Electronics, SSE)。MISP系统由7个安装在防热罩里的集成感应塞组成，每个感应塞包括1个衰退传感器和4个热电偶传感器，用于测量进入大气时的热环境，得到防热罩表面温度分布情况。MEADS由 7个安装在防热罩上的压力测量单元组成(图 1中P1～P7)，测量飞行时防热罩表面的压力分布，在测得进入舱速度的情况下，MEADS的测量数据还可以用于估计当地的大气密度以及风速。MEADS的工作频率为 8Hz，相应的采样周期为 0.125s，从进入大气时开始启动，持续工作至防热罩分离。SSE的任务是为MISP和MEADS提供输入信号，并保存记录相应的测量数据。本文主要介绍MEADS的组成以及相应的估计模型和算法。

根据MSL任务介绍，MEADS的主要任务是单独利用压力的测量值估计进入弹道的气动参数，并要求对攻角和侧滑角的估计偏差不超过 0.5°(3σ)，动压估计偏差不超过 2%(3σ)，马赫数估计偏差不超过0.1(3σ)[5-6]。另一方面，利用机载惯性测量单元(Inertial Measurement Unit, IMU)测量得到舱体角速度和加速度数据后，还可以结合估计得到的气动参数实现对来流密度以及风速的估计，从而建立火星大气模型。

3 数学模型

3.1 表面压力模型

传统的大气参数重建都是基于速管大气数据系统模型(Flush Atmospheric Data System，FADS)进行参数估计，一般采用牛顿流体近似理论建立表面压力分布模型。其中表面压力是测量单元位置、攻角、侧滑角、马赫数等参数的函数。图2即为某个测量单元处速度关于测压管轴线的入射角示意图。

图中，θ为入射角;v为航天器速度。测压管测得的压力包括当地的静压以及沿着测压管轴线方向的动压，即

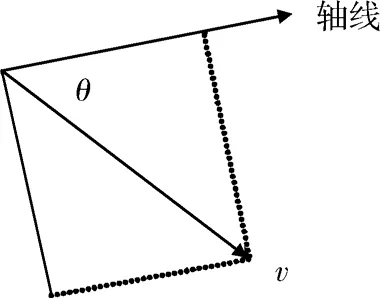
图2 入射角示意图Fig.2 Incidence angle

式中p为某个测量单元的测量值;p∞为当地静压;ρ为当地大气密度;q∞为动压。整理后可得

式中pt为当地的总压;R为静压与总压之比，是马赫数的函数，具体表达式为:

式中γ为比热比;Ma为马赫数。

对于火星大气，取γ=1.335，马赫数与R的函数关系如图3所示:

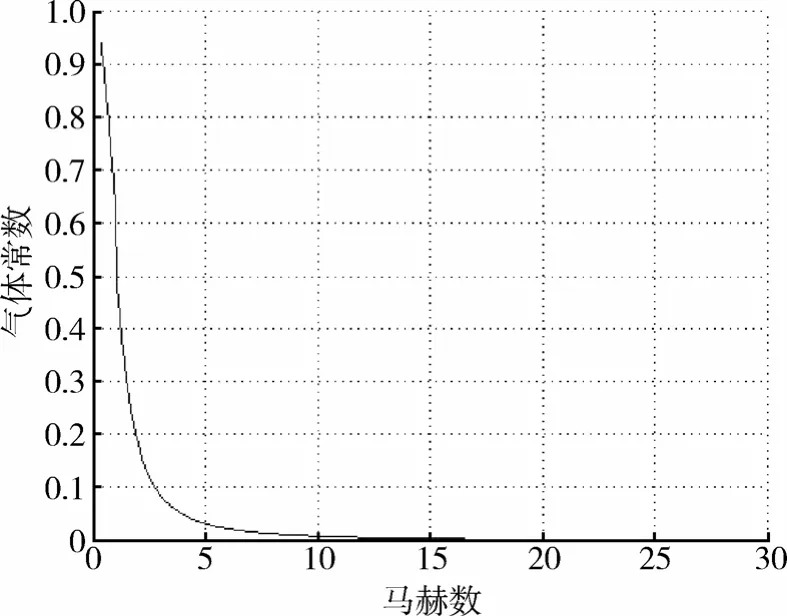
图3 γ=1.335时马赫数与R的函数关系Fig.3 Mach vs pressure ratio R forγ=1.335

入射角θ是压力测量单元位置以及攻角和侧滑角的函数。图4为探测器轴向和侧向视图，显示了其中1个测量单元在防热罩上的安装位置:

图4 测压管安装位置Fig.4 Pressure port geometry

图中，压力测量单元的安装位置由安装锥角λ和指针角φ确定。对于每个测量单元，锥角和指针角均为确定的常数。当进入舱的攻角为α，侧滑角为β时，对图4中的测压单元进行分析，如图5所示:

图5中O-XYZ为进入舱本体坐标系，X轴沿着进入舱纵轴指向前，Z轴在纵向对称面内，垂直于X轴指向上，Y轴由右手坐标系确定。OA为某个压力测量单元的轴线方向，与进入舱的夹角即为锥角λ，OD为进入舱的速度v，OC为速度在OXZ平面的投影，α和β分别为攻角和侧滑角，速度与压力测量单元的轴线夹角θ即为入射角，面AOB与面BOC之间的夹角即为上文定义的指针角φ。

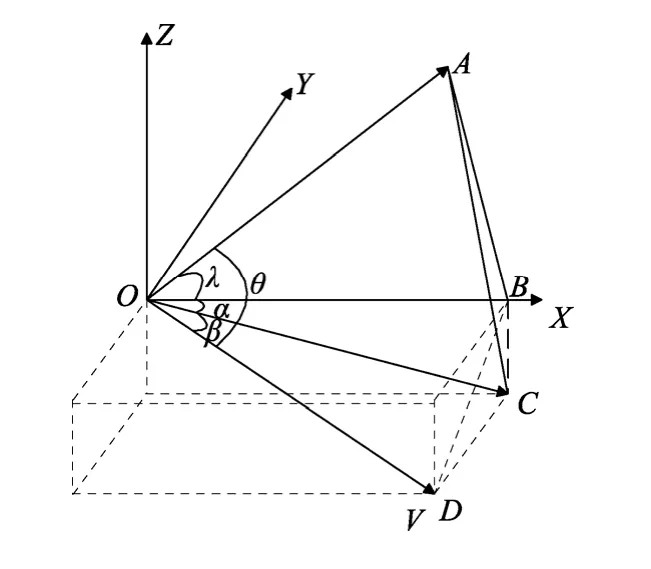
图5 α,β,λ和θ之间的角度关系Fig.5 Relationship betweenα,β,λandθ

在四面角O-ACD、O-ACB中分别利用四面角的余弦和正弦定理可以得到入射角与测量单元位置、攻角以及侧滑角的函数关系为:

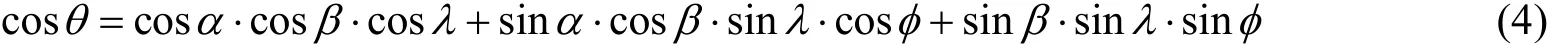
同理，对于其他测量单元，也可以得到与上式类似的关系式(只是安装锥角λ和指针角φ数值不同)。

将公式(3)和公式(4)代入公式(2)就可以得到某个测量单元测得的压力值关于测量点位置、总压、马赫数、攻角以及侧滑角的函数关系，将7个测量单元的关系式组成1个函数方程组，即为表面压力分布模型。

综上，基于传统的速管大气数据系统模型，通过推导测压单元测量值与安装位置之间的函数关系，建立了MSL防热罩表面的压力分布模型，用于下文的状态估计。

3.2 卡尔曼滤波

上文已经建立了表面压力分布模型，在此基础上利用卡尔曼滤波估计气动参数和大气参数。卡尔曼滤波器可以将MEADS和IMU测量结果通过一种紧耦合的方式直接融合，从而利用MEADS测量的压力值和IMU测量得到的加速度及角速度值直接估计大气数据和气动参数，其优越性主要体现在可以通过反复迭代基本消除测量噪声的影响，从而利用有限的量测值估计得到精度较高的状态量。实现的方法是将压力模型改写为来流气动特性(压力、密度、风速)和空速的函数，构建量测方程，计算得到这些中间变量之后，攻角、侧滑角、马赫数以及动压也可以进一步计算得到[7]。

基于这种思路，滤波器选择的状态变量x为:

式中r为进入舱质心到火星质心距离;φ是赤维;ei为水平坐标系到本体坐标系的变换四元数[8];u,v,w分别为进入舱地速在当地水平坐标系中的投影;uw,vw,ww为风速在当地水平坐标系中的投影。

将图5中进入舱空速投影到本体坐标系上，沿3个轴的投影值分别为ub,vb,wb。则气动参数(攻角、侧滑角)可以表示为:

ub,vb,wb同时也是风速和进入轨道的函数:

式中Ψ,,ΘΦ分别为本体坐标系相对于当地水平坐标系(北东下坐标系)的偏航角、俯仰角、滚转角;G为相应的转移矩阵。

联立公式(1)和公式(4)可得:

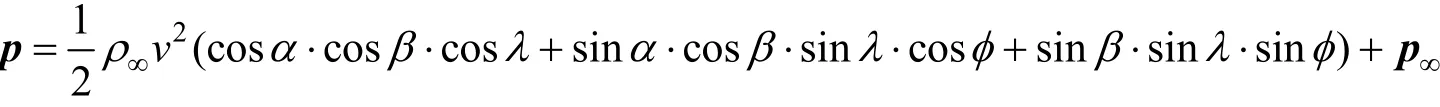
上式中再利用式(5)和式(6)中攻角、侧滑角与当地水平坐标系中u,v,w,uw,vw,ww以及欧拉角之间的关系就可以得到一个测量点量测方程，将所有测量点的量测方程联立为量测方程组，将该量测方程组离散化，即将k=1,2,3,…时刻的量测值表示为每个时刻状态向量和量测噪声的函数hk:

式中pk为k时刻的所有测量点测量值矩阵;xk为k时刻状态向量;vk为k时刻的量测噪声。

滤波器动力学方程(状态方程)如下所述:

式中μ为火星的引力常量;φ为赤纬; 矩阵G为当地水平坐标系到本体坐标系的转移矩阵;xω，yω和ωz为IMU测量得到的本体坐标系中3个坐标轴方向的转动角速度;au，av和aw是进入舱质心加速度在本体系中的投影，与IMU测量的IMU单元安装支架处的加速度之间的关系为:

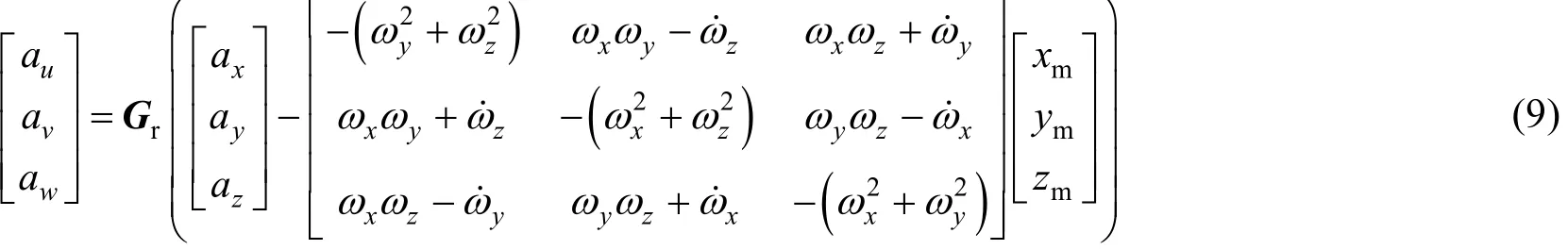
式中ax，ay和az为IMU测量得到的加速度分量;xm，ym和zm为IMU在本体坐标系中的安装位置;Gr为IMU坐标系到本体坐标系的转移矩阵。

于是滤波器状态方程和量测方程分别可以表示为:

式中w是分别是系统过程噪声;Rk为量测噪声协方差;Q为过程噪声协方差;f为状态量微分关系。

由状态方程可以看出，系统过程噪声主要指的是IMU的测量噪声，由IMU性能决定，属于零均值高斯白噪声[9]。量测方程中，量测噪声主要来自于测量单元的安装误差和测量时间误差。其中测量单元的安装误差为15mm(3σ)，可以换算成安装锥角λ和指针角φ的偏差，均为零均值高斯白噪声; 测量时间误差指的是不同测量单元测量得到同一组压力值时的时间差，包括系统固有误差以及随机偏差。其中，固有误差可以通过地面试验进行矫正，随机误差约为±0.025s(3σ)，同样为零均值白噪声，符合卡尔曼滤波器的要求[10]。

滤波器初值设定为:

式中为零时刻状态量的后验估计，等于状态量初值的均值E(x0)。

式中为零时刻状态量估计误差协方差;表示对x0的估计。

对于每个k，执行如下递推计算:

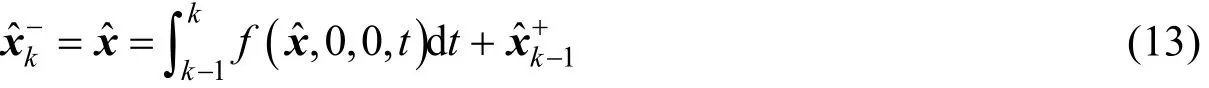
式中为k时刻状态量的先验估计;为k时刻状态量的后验估计。

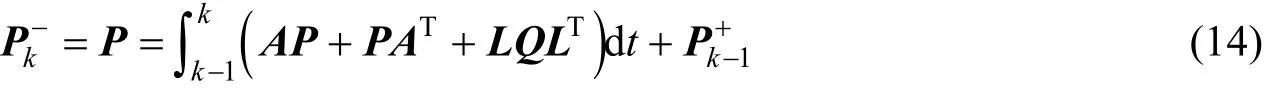
式中=P为k时刻先验状态估计协方差;为k时刻后验状态估计协方差;为状态转移矩阵;为噪声转移矩阵。

式中Hk,i为k时刻第i次迭代测量值关于状态量的偏微分矩阵。

式中Mk,i为k时刻第i次迭代的测量噪声转移矩阵。

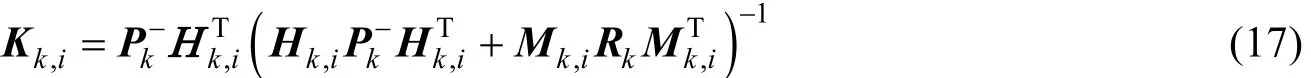
式中Κk,i为k时刻第i次迭代的增益矩阵。

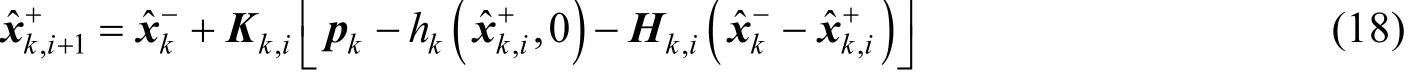
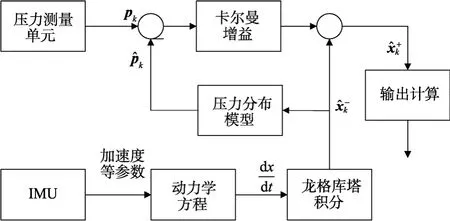
图6 卡尔曼滤波流程Fig. 6 Rocess of the Kalman Filter

4 精度分析

上文中，基于卡尔曼滤波建立了用于估计气动参数和大气参数的拓展卡尔曼滤波器。由于目前无法获得量测值以及部分由IMU测得的状态量，为了研究卡尔曼滤波器的估计精度，选择部分状态量(X、Y、Z位置矢量)，利用上述滤波器对进入舱进行轨道位置估计，与弹道仿真的轨道信息对比计算位置误差，并与最小二乘的估计误差进行比较，其结果如图7所示:

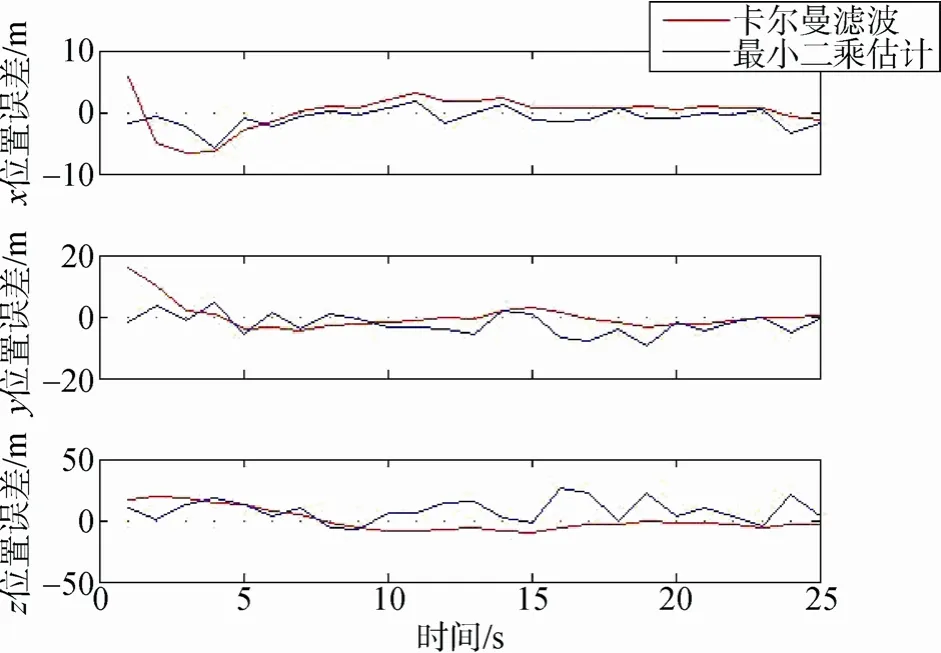
图7 卡尔曼滤波误差Fig. 7 Errors of the Kalman Filter

由上图可以看出，相比于普通的最小二乘法状态估计，卡尔曼滤波器的估计误差更小，经过约 10s时间误差基本收敛为零，最大误差不超过10m，具有一定的优越性。因此，可以将卡尔曼滤波方法应用于火星探测中进入弹道和大气模型重建。

5 结束语

本文首先对“火星科学实验室”的MEADS系统的组成以进行了介绍，以此为基础详讨论了表面压力分布模型的建立过程。通过在防热罩上安装的7个压力测量单元，可以测得进入火星大气过程中进入舱表面的压力分布情况。若探测器安装了用于姿态轨道控制的机载IMU设备，就可以利用表面压力分布模型和IMU测量值，通过迭代卡尔曼滤波比较精确的计算每个时刻火星探测器的气动参数和周围大气的密度和静压。这一方面可以重建较精确的进入弹道用于任务分析，也可以估计得到进入段的大气密度以及静压随高度的变化情况，建立火星大气模型。本文的研究可以为将来我国开展火星探测以及建立火星大气模型提供一定的参考依据。

References)

[1] 欧阳自远, 李春来. 深空探测的进展与我国深空探测的发展战略[C]. 2002年国际深空探测技术和应用会议论文集，2002.OU Yangziyuan, LI Chunlai. Progress of Deep Space Exploration and Development Strategy in China[C]. The Deep Space Exploration Technology and Application Conference Proceedings, 2002.(in Chinese)

[2] 荣伟, 陈旭, 陈国良. 火星探测着陆系统开伞控制方法研究[J]. 航天返回与遥感, 2007, 28(4): 6–11.RONG Wei, CHEN Xu, CHEN Guoliang. The Control Method Study on the Parachute Deployment for the Mars Exploration Landing System[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 6–11. (in Chinese)

[3] Christopher D K, Roger E B. Mars Entry Atmospheric Data System Modeling and Algorithm Development[R].NASA-0025419, 2009.

[4] Gazarik M J, Wright M J. Overview of the MEDLI Project[C]. IEEE 2008 Aerospace Conference, 2008.

[5] Pruett C D, Wolf H, Heck M L. Innovative Air Data System for the Space Shuttle Orbiter[J]. Journal of Spacecraft and Rockets,1983, 20(1): 61–69.

[6] Siemers P M, Henry M W, Eades J B. Shuttle Entry Air Data System(SEADS)-advanced Air Data System Results: Air Data Across the Entry Speed Range[R]. NASA CP-3248, 1995.

[7] Kasich D C, Cheng P Y. Flush Port/Inertially Blended Air Data Estimator[C]. AIAA-910670, 1991.

[8] John A C, Amanda M V, Robert D B. Tatistical Reconstruction of Mars Entry, Descent, and Landing Trajectories of Atmospheric Profiles[C]. AIAA-6192, 2007.

[9] Karlgaard C D, Tartabini P V, Blanchard R C. Hyper-X Post-flight Trajectory Reconstruction[J]. Journal of Spacecraft and Rockets, 2006, 43(1): 105–115.

[10] Dan S. Optimal State Estimation[M]. Cleveland State University: John Wiley & Sons, Inc, 2006.