变压器谐波模型的研究与评价

方少麟，李建华，黄 莹，邱 伟，桑天松

（1.西安交通大学电气工程学院，西安710049；2.南方电网科学研究院，广州510080）

变压器是电力系统中的重要元件之一，谐波下其数学模型的准确程度直接影响到电力系统谐波分析与计算的准确性。虽然工频下已有公认的变压器模型，但随着频率的升高，这些模型将不再适用，因此，寻求准确的变压器谐波模型对于谐波研究有着重要的意义。

在对电网进行谐波潮流计算或谐波阻抗计算时，往往只给出各变压器在基波下的电抗与电阻，如何利用基波下的阻抗值合理地表示谐波下变压器的特性，是谐波下变压器建模的关键。

工频下的变压器模型，一般不考虑励磁支路的影响，直接将变压器绕线电阻与漏抗串联来表示变压器模型。但随着频率的升高，铁心中的涡流损耗及其他附加损耗增加，励磁支路的影响将不能忽略[1]。谐波分析中，一般也采用绕线电阻与漏抗串联的变压器模型，但为了考虑导线集肤效应或铁心损耗的影响，模型中的串联电阻将是频率的函数[2～5]；也有学者提出采用电阻与漏抗并联来建立变压器的谐波模型[5，6]。这些模型在频率特性上差别很大，但目前用于系统谐波分析与计算方面的变压器谐波模型的理论性研究不够，相关文献中并没给出各模型的适用条件。

国内外许多学者对变压器谐波模型的建立提出了相应的方法。文献[7-9]分别论述了各自方法的优缺点，但可看出变压器谐波电阻随频率的升高显著升高，电感随频率的升高逐渐下降的特性。文献[10]采用指数与多项式的表达式来表述换流变压器谐波阻抗与基波阻抗的关系，有一定的指导意义，但由于其研究对象为换流变压器，未必适用于普通电力变压器，因此需对电力变压器进行进一步研究。文献[11]对于变压器在谐波下的有功损耗和漏磁场的磁效应进行了深入研究，并得到较为适用的损耗估算方法。在某频率下，变压器整体消耗的有功功率对应于在该频率下变压器的等效电阻。文献[12]采用该方法计算了变压器的涡流损耗，与测量结果基本相符，证实了该方法的准确性。本文在文献[11]的基础上，提出考虑谐波下变压器各部分铁耗和铜耗对应其谐波有效电阻的方法来建立变压器谐波模型，并以此作为变压器谐波模型的参考模型；对常用的六种变压器谐波模型进行理论分析，得到最合理的谐波模型；并对两类变压器实例进行计算，将常用模型与参考模型进行对比，验证目前常用变压器谐波模型的适用性。

1 变压器频率特性

在某特定频率下，变压器所消耗的有功功率，为其相应频率等效电阻上消耗的有功功率。因此，通过计算不同频率下变压器的有功功率损耗，即可求出变压器的谐波等效电阻。

变压器的谐波损耗主要由铁耗和铜耗两部分组成。铁耗与频率存在着较大关系，因此在建立谐波模型时，应充分考虑到铁耗的影响。铁耗主要由磁滞损耗、涡流损耗和铁心附加损耗三部分组成。其中，磁滞损耗与频率成正比，涡流损耗与频率平方成正比，这两部分是由硅钢片材料决定。铁心附加损耗由设计结构及加工等原因引起，可引进一个附加系数来考虑附加损耗。在基波工作条件下，频率相对较低，变压器铜耗占有功损耗的主要部分。但在谐波分析时，由于频率逐渐提高，导线内部电流的不均匀分布和去磁作用的影响越来越显著，在建立变压器模型时，也应予以考虑。

按什捷因麦茨公式[11]，可计算出磁滞损耗和涡流损耗，其表达式为

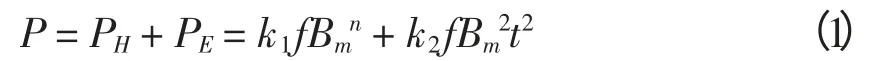
式中：PH为磁滞损耗；PE为涡流损耗；f 为电压的频率；Bm为磁通密度幅值；t 为矽钢片厚度；k1和k2取决于矽钢的特性。

当外施电源频率提高时，矽钢片中涡流的去磁效应会显现出来，即矽钢片中部的磁通被排挤到边缘，这种现象也称作磁通的排挤效应。涡流的去磁效应使得涡流损耗降低的数值是矽钢片厚度、频率、钢片磁导率和电导率的函数[11]，即

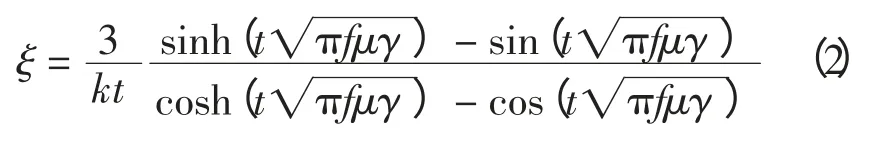
式中：f 为频率；μ 为磁导率；γ 为电导率。

漏磁通在变压器的油箱壁、压板、夹件和其它大质量的铁磁介质零件里产生涡流损耗和磁滞损耗，其中涡流损耗起决定性作用。对于变压器所有结构元件里的涡流损耗之和的计算，一直沿用公式[11]为

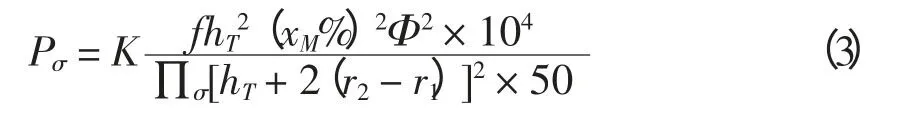
式中：hT为线圈高度；f 为电压的频率；xM%为变压器短路感抗的相对值；Φ 为每柱磁通；∏σ为油箱周长；K 为经验系数；r1为漏磁通主空道的平均半径；r2为油箱的平均半径。

由式（3）可以看出，漏磁场引起的有功损耗与频率成正比。

变压器的漏磁场在线圈导线里感应出电动势，在此电动势作用下将产生电流。即在线圈导线里除了存在负载电流之外，还存在着漏磁场所引起的电流，这个电流在各导线内部闭合，与负载电流不同，它并不流出线圈以外去。这就使得电流密度沿线圈导线横截面的分布以及各并联导线间的电流分布变得不均匀，这种现象也称作电流的排挤效应。这些电流建立自身的磁场，削弱变压器的漏磁场，即存在一定的去磁作用。

由于以上原因，随频率的增加，线圈的实际电阻比通过直流电流时的电阻大为增加，用系数kr表示实际电阻与直流电阻之比；这些电流产生的磁场能大大削弱线圈所在空间的漏磁场，使线圈感抗减小，用系数kx表示考虑去磁作用后的漏抗与不考虑去磁作用漏抗之比。电阻增大及电感减小的系数计算式[11]为

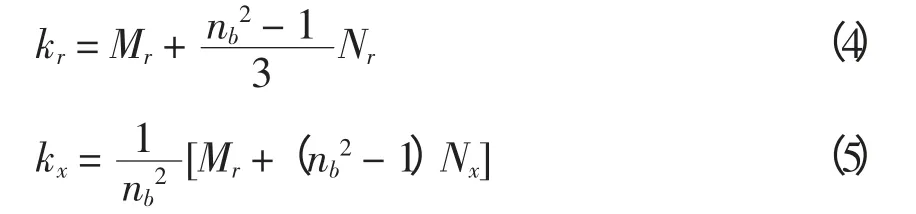
式中：nb为径向方向导线根数，kr>1，kx<1。

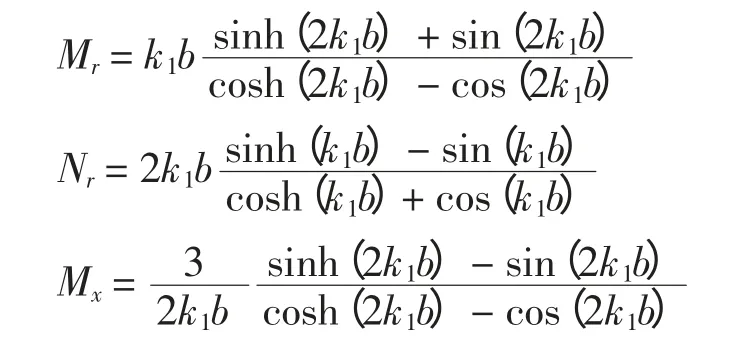
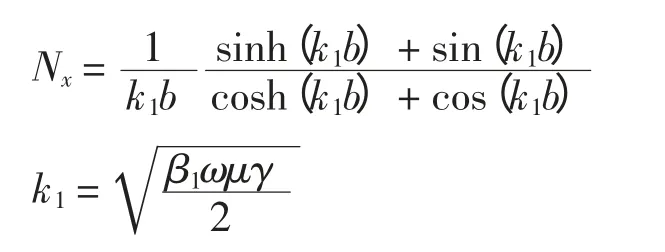
由于载流导体并没有占据线圈高度上的全部空间，以β1表示载流导体占据的实际高度与线圈高度之比；b 为导体的辐向尺寸。

综上所述，在谐波分析时，变压器模型的谐波电阻需要考虑以上各种变压器损耗的影响。包括铁心磁滞损耗、铁心涡流损耗、铁心附加损耗、绕组负载电流引起的损耗、漏磁场在导线内引起的涡流损耗以及在结构元件中引起的涡流损耗。谐波电抗需要考虑到导线中涡流的去磁作用。在以上分析的基础上，本文提出一种较为全面的变压器谐波模型，由电阻与电抗串联组成，电阻和电抗表达式分别为

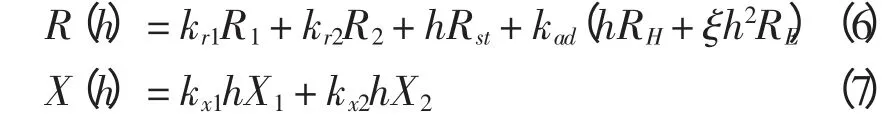
式中：h 为谐波次数；R1为一次侧绕组直流电阻；R2为二次侧绕组直流电阻；Rst为结构元件铁耗等效电阻，可根据式（3）工频下的有功损耗来计算；RH为磁滞损耗等效电阻，可根据式（1）工频下的磁滞损耗来计算；RE为涡流损耗等效电阻，可根据式（1）工频下的涡流损耗来计算；kad为附加损耗系数，表示铁心附加损耗，这里取1.25；X1为一次侧绕组漏抗；X2为二次侧绕组漏抗；kr1为一次侧绕组电阻排挤系数，kr2为二次侧绕组电阻排挤系数，kr1和kr2由式（4）来计算，表示绕组导线内电流不均匀分布而引起交流电阻增大的系数；kx1为一次侧绕组电抗排挤系数，kx2为二次侧绕组电抗排挤系数，kx1和kx2由式（5）来计算，表示漏磁场在绕组导线内感生的涡流存在去磁作用而引起漏感减小的系数；ξ 为铁心去磁系数，由式（2）来计算，表示铁心中涡流的去磁效应使得涡流损耗减小的系数。

上述分析可知，针对电力系统的谐波分析与计算，本文提出的变压器谐波模型，比其他常用变压器谐波模型包含了更全面的影响因素，考虑了多种与变压器谐波参数相对应的有功损耗以及铁心和绕组涡流的去磁效应，理论上更为准确。但该模型要求已知过多的变压器参数，而且其中的部分参数不易获得。因此该方法只适于理论分析及已获得大量信息的特定变压器的谐波建模，而不适用于对大量不同类型变压器的谐波建模。故这里将该变压器谐波模型作为理想的参考模型，以此检验目前常用变压器谐波模型的适用性。

2 常用变压器谐波模型分析

在进行电网谐波计算时，通常只了解各个变压器的部分信息，比如工频阻抗，难以通过上述方法进行变压器建模，为了进行谐波计算，通常只能根据基频下的部分参数（如电阻、电抗和功率）来进行建模。目前常用的变压器模型如下。

模型1 变压器电阻与频率的平方根成正比[3]

模型2 变压器电阻与频率成正比[4]

模型3 变压器谐波损耗的增量与频率的1.5次方成正比[1]

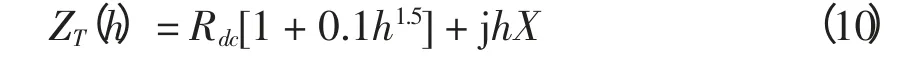
由于变压器损耗与频率存在着复杂的关系，以上三种表述均不够准确，并没有充分考虑到铁心损耗的影响。在低频下差别虽然很小，但随着频率的升高，差距会明显增大。

模型4 引入磁滞涡流系数J 来考虑铁耗影响[5]

其中J 为磁滞涡流损耗，对硅钢取3，k=1/（J+1）

前四种模型都没有考虑到随着频率增加，导线内感生涡流的去磁作用使得漏感减小的影响。

模型5 等值电路如图1 所示[5]。

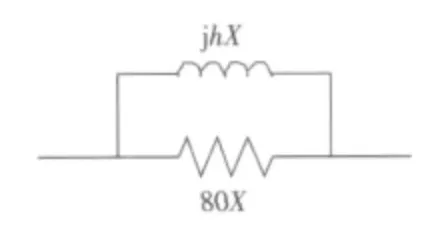
模型6 等值电路如图2 所示[6]。

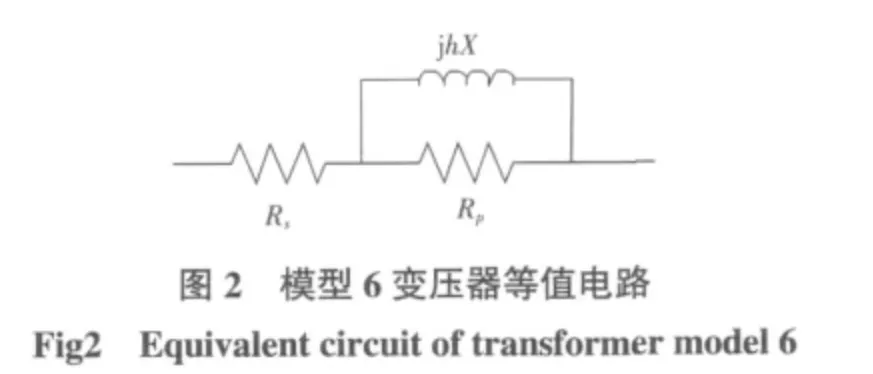
X 为50 Hz 时的变压器漏抗，Rp和Rs不随频率的变化而变化，其中：

模型5 和模型6 中，都含有电阻与电抗并联的部分。

对于模型5

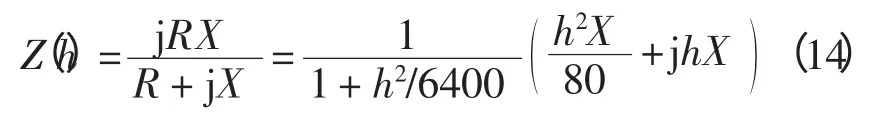
对于模型6

绕组导线中占主导作用的涡流损耗都近似与频率的平方成正比，因此可用模型5 中h2X/80 和模型6 中h2X/10tan φ 表示这部分损耗。电抗与频率成正比，因此用jhX 表示电抗，但随着频率的升高，绕组导线和铁心中涡流都会起到去磁效应，使得导线中的涡流损耗、铁心中的涡流损耗和漏感出现一定程度的减小，模型5 和模型6 采用（1 +h2/6400）-1和（1+（h/10tan φ）2）-1来考虑去磁效应，在频率较低时，去磁效应较弱，这两项影响可忽略，但随着频率的升高，去磁效应逐渐加强，这两项才会体现出去磁的作用。在低频下，绕组导线的欧姆损耗仍是总损耗的主导部分，模型5 中只计及了导线和铁心的涡流损耗，没考虑欧姆损耗，因此在低频时，模型5 的电阻值应呈现出偏小的趋势。而模型6 中则通过串联一个电阻来表示导线绕组的欧姆电阻，而且根据不同容量的变压器，其采用不同阻抗角来计算导线阻抗，更为合理。

3 模型验证

推荐模型的计算需负载损耗、空载损耗、结构件损耗和绕组导线规格等参数，在电力系统谐波分析及计算时，常采用电网潮流计算数据，因此上述参数难以获得。因此采用推荐模型作为参考模型，以此来研究六种常用模型的适用性。本文以SF9-25000/110 型变压器和SZ9-3150/35 型变压器为例，来验证以上六种常用变压器谐波模型的适用性，两种变压器的技术参数如表1[13]所示。以式（6）和（7）为参考模型，将六种模型共同绘制出其频率特性曲线，并与参考模型的频率特性进行对比，计算频率为电网谐波分析常关注的频率区间50 Hz～2500 Hz，计算结果如图3～图8 所示。

从图3～图8 中的实线为本文提出的变压器谐波参考模型的计算结果，该模型由于考虑了变压器各部分的铁耗和铜耗，同时考虑了绕组导线内涡流的去磁效应，因此更为接近于变压器在谐波下运行的实际情况。这里将该参考模型作为基准，其它六种常用模型与该参考模型进行对比，以检验其适用性。由参考模型的计算结果可知，随着频率的升高，由于铁耗和铜耗的存在，会使得变压器谐波等效电阻显著增加，由于绕组导线中涡流的去磁作用，漏感也会显著地减小，因此在建立变压器谐波模型时，有必要考虑这两个因素。

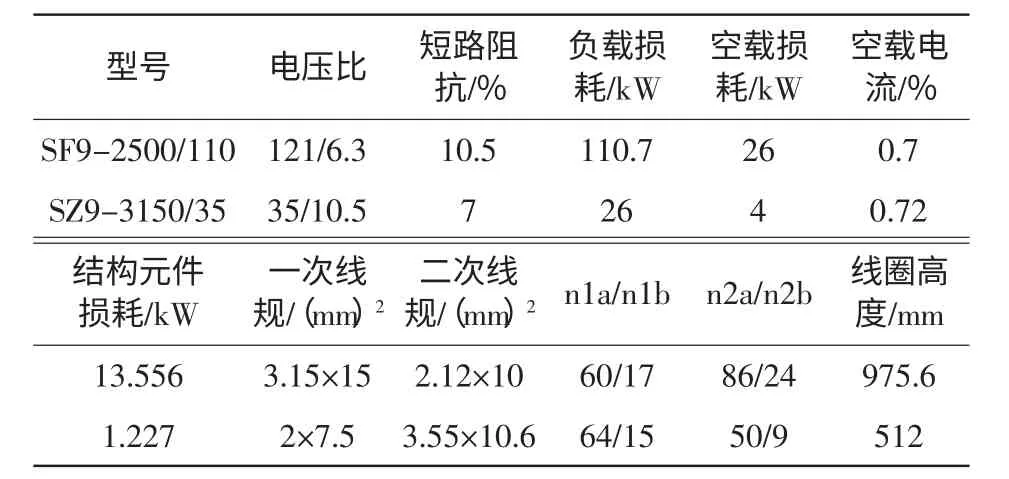
表1 变压器技术数据Tab.1 Technique data of transformer

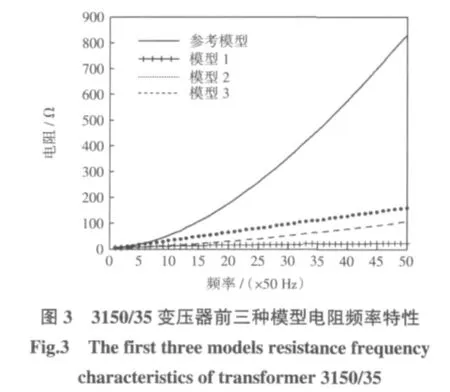
由图3 和图6 可知，模型1、模型2 和模型3，其电阻的频率特性曲线远小于参考模型电阻的频率特性曲线，由前面分析可知，变压器谐波模型1和模型3 只在工频附近与参考模型比较接近；模型2 在300 Hz 以下时与参考模型比较接近。随着频率的升高，前三种模型的计算结果与参考模型之间的偏差越来越显著，这是由于没有充分考虑铁芯和绕组导线中涡流损耗影响所致，不够准确。

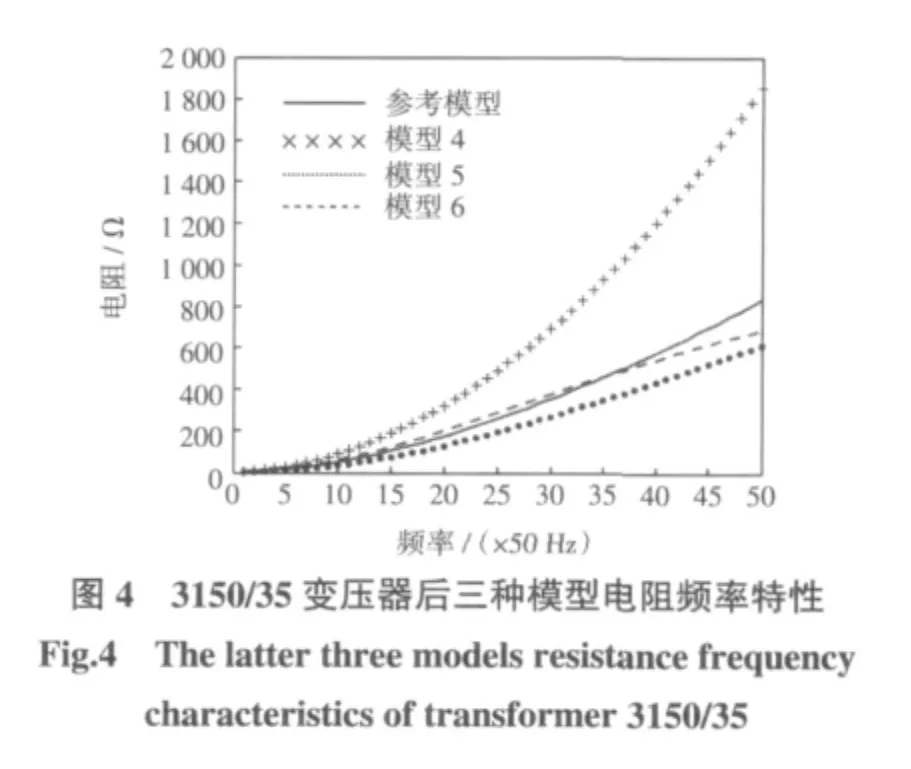
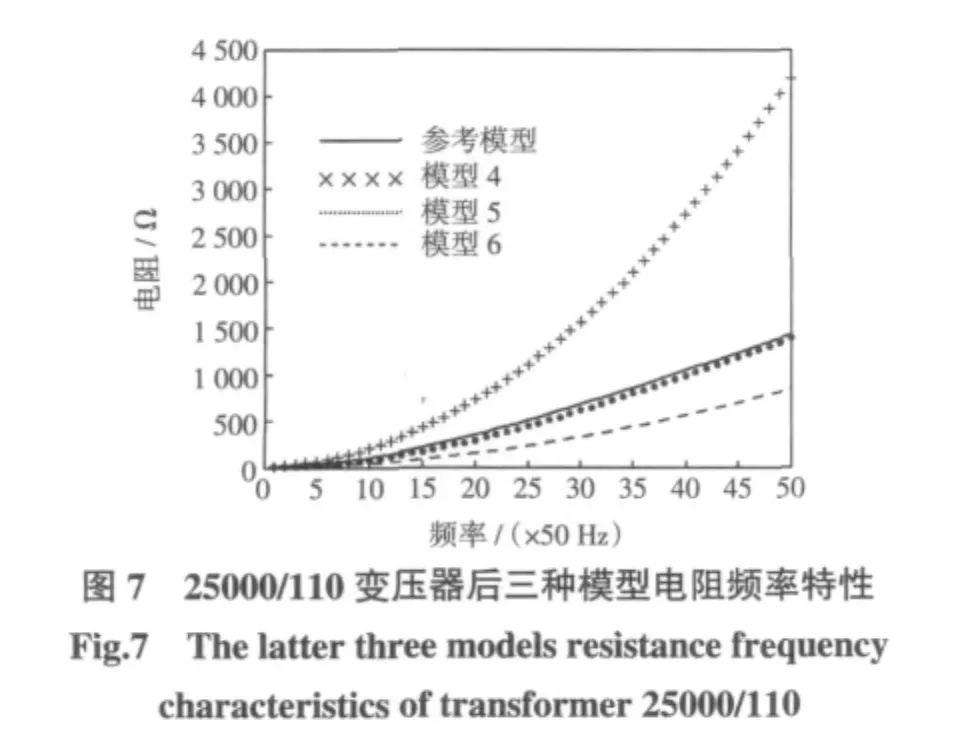
由图4 和图7 可知，模型4 虽然考虑铁耗的影响，但其并没有区分铁耗中涡流损耗和磁滞损耗与频率呈不同的函数关系，将铁芯磁滞损耗和涡流损耗一起当作与频率的平方成正比进行处理，而且对于涡流损耗，也没考虑去磁作用。在300 Hz 以下，由于涡流损耗的作用还不明显，因此模型4 与参考模型较接近。随频率的升高，其电阻值增长较快，在2500 Hz 时，为参考模型阻值的2～3 倍。模型5 与模型6，与前文理论分析的结果相同，由于考虑了变压器绕组导线和铁芯中占主导作用的涡流损耗，同时还考虑到了涡流去磁效应的作用，其阻值与参考模型得到的阻值比较接近。

对于SF9-25000/110 和SZ9-3150/35 两种型号的变压器，低频时，模型5 没有考虑绕组导线的直流电阻，存在一定误差，工频时其电阻仅为参考模型电阻的0.09～0.2 倍；模型6 的计算结果，更接近于参考模型，其电阻为参考模型的1.1～1.6 倍，这与前面的分析完全吻合，即模型6 中串联电阻在低频时能够有效地模拟导线绕组的欧姆电阻，并且这部分电阻在低频时占到了变压器全部电阻的主要部分。在中、高频时，模型5 的计算结果更接近于参考模型。

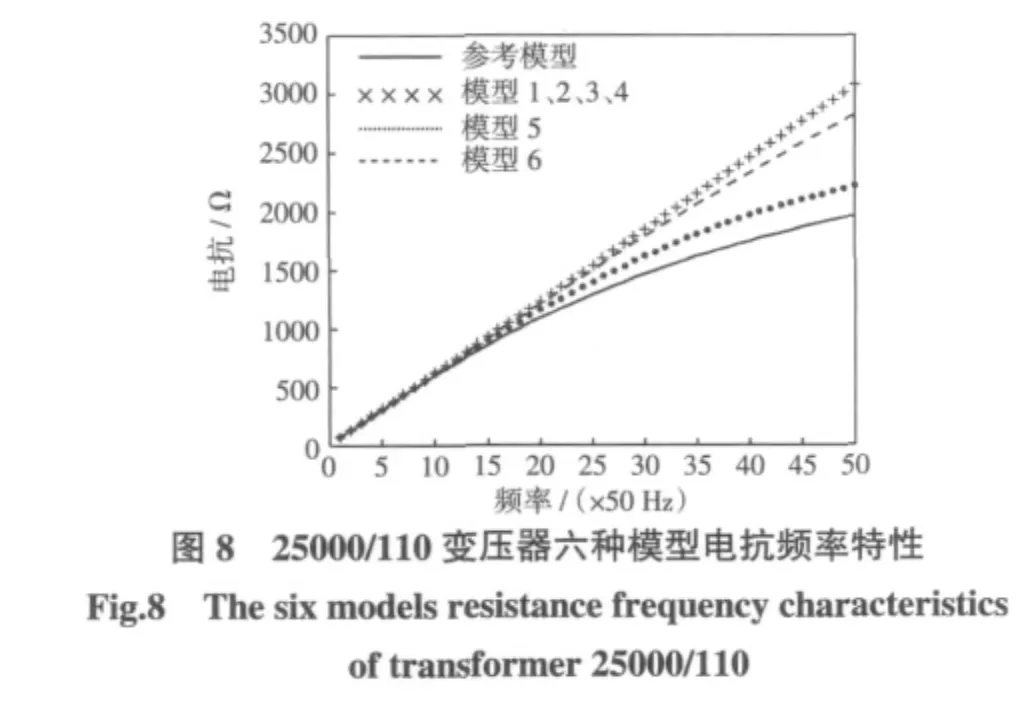
由图5 和图8 可知，由于参考模型考虑了绕组导线中涡流的去磁作用，因此在高频时，会呈现漏感显著下降的趋势。在500 Hz 以下，绕组导线内涡流的去磁作用非常小，可以忽略不计；在500 Hz～1 000 Hz 之间，去磁作用逐渐显现，使得漏感略微减小；在1 000 Hz 以上时，去磁作用愈发显著，必须要考虑去磁的作用。模型1、模型2、模型3 和模型4，其电抗与频率呈现严格的线性关系，并没有考虑到频率升高时，导线中涡流的去磁作用。而模型5 和模型6 中，考虑导线中涡流的去磁效应，因此其漏电感随着频率的升高，出现逐渐下降的趋势，在一定程度上反映了涡流的去磁效应。

由于本文提出的变压器谐波模型是基于功率与电阻等效关系的理论公式，其计算结果与变压器实际情况可能存在一定误差，但随着频率升高，变压器等效电阻显著增加，等效电抗逐渐减小的趋势与实际情况应是相符的。模型5 和模型6 在50 Hz～2 500 Hz 频率区间内，其反映出电阻增大与电抗减小的趋势与参考模型相一致，因此模型5与模型6 都可较为准确地模拟变压器的谐波特性。相比，模型6 在低频时更准确，而模型5 在本文所采用的两个变压器算例中，在高频时更准确。在300 Hz 以下时，由于铁耗的作用和导线内涡流的去磁效应还不够明显，也可用模型2 和模型4来模拟变压器的谐波特性。而模型1 和模型3，只适用于100 Hz 以下的变压器谐波建模。但随着频率的升高，前四种变压器谐波模型不再适用。

4 结语

本文根据变压器在某特定频率下所消耗的有功功率来计算谐波等效电阻，根据漏磁场的去磁效应，计算谐波等效电抗，以此提出一种变压器谐波模型。该模型需较多变压器结构参数，不易获得，因此难以在工程上使用，但可作为参考模型检验其它变压器谐波模型的适用性。本文分析了六种常用变压器谐波模型的特点及合理性。指出模型5 和模型6 由于考虑了导线的涡流损耗、电流排挤效应、铁心损耗及涡流的去磁效应，因此更准确。二者相比，模型6 考虑了基波的铜耗，因此在低频时更准确。通过对两种类型变压器实例计算，进行了模型验证，计算频率区间为50 Hz～2 500 Hz，其计算结果与理论分析一致，模型5 和模型6 与参考模型更接近。因此，在电网谐波分析与计算中，可采用模型5 和模型6 来模拟变压器谐波模型。

[1]Mahmoud A A，Shultz R D. A method for analyzing harmonic distribution in AC power systems [J].IEEE Trans on Power Apparatus and Systems, 1982，l01（6）：1815-1824.

[2]Farncisco C，De La Rosa. Harmonics and Power Systems[M].北京：机械工业出版社,2009.

[3]Arrillaga J，Watson N R.Power System Harmonics[M]. 北京：中国电力出版社,2008.

[4]Wakileh G J. Power System Harmonics Fundamentals，Analysis and Filter Design [M].北京：机械工业出版社，2011.

[5]Densem T J，Bodger P S，Arrillaga J. Three phase transmission system modelling for harmonic penetration studies[J]. IEEE Trans on Power Apparatus and Systems，1984，l03（2）：310-317.

[6]Wu Xueguang，Sadullah S，Matthews B，et al. Nodal harmonic impedance derivation of AC network in PSS/E[C]//9th IET International Conference on AC and DC Power Transmission.London，UK：2010.

[7]王瑞珍，刘丰，于育民（Wang Ruizhen,Liu Feng，Yu Yumin）. 换流变压器谐波损耗频率特性测量方法研究（Research on measuring method of frequency characteristic of harmonic losses in convertor transformers）[J]. 变 压器（Transformer），2002,39（1）：24-27.

[8]Hwang M S，Grady W M，Sanders H W Jr. Distribution transformer winding losses due to nonsinusoidal currents[J]. IEEE Trans on Power Delivery，1987，PWRD-2（1）：140-146.

[9]Li Pei，Li Guodong，Xu Yonghai，et al. Methods comparation and simulation of transformer harmonic losses[C]//Asia-Pacific Power and Energy Engineering Conference.Chengdu，China：2010.

[10]兰丽霞，徐向军，罗隆福（Lan Lixia,Xu Xiangjun,Luo Longfu）.新型换流变压器谐波损耗的计算与分析（Calculation and analysis of new type converting transformer's harmonic loss）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（6）：36-40.

[11]瓦修京斯基C B.变压器的理论与计算[M].北京：机械工业出版社，1983.

[12]Crepaz S. Eddy-current losses in rectifier transformers[J].IEEE Trans on Power Apparatus and Systems，1970，89（7）：1651-1656.

[13]刘传彝.电力变压器设计计算方法与实践[M].沈阳：辽宁科学技术出版社，2005.