城市生态系统指标相互影响的定量研究

马寨璞，安秋丹，刘庆朝

（河北大学 生命科学学院，河北 保定 071002）

城市生态系统是一个复杂的系统，目前，对城市生态系统的研究主要集中在应用数学理论对城市指标体系进行等级划分，进而根据等级划分情况对城市的生态环境进行现状评价，并研究各个子系统在城市可持续发展方向对城市生态系统的贡献，这些理论方法包括BP神经网络［1］、层次分析法［2］、模糊数学理论［3－4］、基于属性理论［5］等.具体研究涉及很多方面，例如对环境质量的评价［1，3］、环境与经济协调发展的不确定性评价［6］、对生态系统的健康评价［5，7－8］，对城市生态系统现状的生命力指数的研究［9］.此外，还有人将地理信息系统应用在对城市宜居性的评价中［10］.

城市生态系统包含众多子系统及指标，如果将每一个系统子项看作一个节点，那么城市生态系统就构成了一个复杂网络.本文探讨应用网络理论对城市生态系统进行分析，建立了城市生态系统网络模型，归纳了城市生态网的定义，并通过网络模型探讨了城市生态系统中各因子之间的关系.

1 构建城市生态系统指标体系并建立城市生态网

1.1 城市生态系统指标体系构成

城市生态系统涉及自然、经济、社会3大子系统.各子系统由不同的组分构成，各组分由不同的指标加以评价.

本文选择了39个具有代表性的能够概述3大子系统的评价指标，其中自然系统包括空气污染指数等9个指标，经济系统包括研究与试验发展经费（R＆D经费）等11个指标，社会系统包括环保投资占GDP比例等19个指标.

1.2 建立城市生态网

1.2.1 节点指标选定与数据准备

城市发展水平不同，根据《中国中小城市发展报告（2010）：中国中小城市绿色发展之路》有关城市划分的标准［11］，将中国国内城市分为3类，即一线城市（特大型）、二线城市（大型）、三线城市（中小型）.其中一线城市包括北京、天津和上海等；二线城市包括南京、武汉和沈阳等；三线城市包括银川、吉林和大庆等.中国国内城市众多，本文选取了21个具有代表性的城市，其中一线城市5个，二线城市和三线城市各8个.各城市数据来源主要取自《2009年中国城市统计年鉴》［12］，人均可支配收入和恩格尔系数2个指标取自各城市2009年统计年鉴.居民人均年生活用水、人均年生活用电量、人均居住面积、万人拥有床位数、万人拥有影剧院数、万人拥有教师数、人均邮电业务总量、工业废水排放达标率和恩格尔系数等9个指标的数据通过计算获得.土地产出率和环保投资占GDP比例2个指标数据缺失，本文分别用相近的第一产业占GDP比例、三废综合利用产品产值来代替，并将三废综合利用产品产值归入经济系统.最终选定26个指标，如图1.

图1 城市生态网选定指标Fig.1 Selected indicators of urban ecological system

1.2.2 节点指标相关性计算

构建城市生态网，首先要确定各指标之间是否具有关系，以及具有何种关系.在确定各指标之间的关系时，本文采取3种手段加以确定：1）参考已有文献，对联系明确的指标直接连接；2）依据生态学基础知识连接各指标节点；3）对未定关系的指标采用数理统计的方法加以确定.

在讨论各节点（指标）之间关系时，需要计算相关节点（指标）间权重.数理统计中，在多元线性逐步回归分析得到的最优方程中，偏回归系数表达了自变量对因变量的具体效应，通过对偏回归系数进行标准化，可得到直接反映自变量相对重要性的权重值［13］.本文针对选定的26个指标，进行了多元线性逐步回归分析，得到了各指标之间关系及权重.由于一线城市太少，样本太小，故未进行回归.二、三线城市回归得到的权重标在图2，3上，各数据均进行了显著性检验.

1.2.3 建立城市生态网

将每一个系统指标看作一个节点，以带有方向的曲线连接相关的各节点，以自变量xi为曲线始点，箭头指向因变量xj，则城市生态系统构成一个复杂的网络.

依据回归结果所得各节点之间的关系建立城市生态网.图2是二线城市的生态网络图，图3是三线城市的生态网络图，在图2，3中，xi（i＝1，2，3，…，26）分别代表前述26个指标.

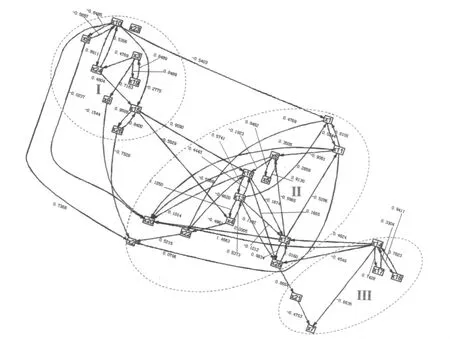
图2 二线城市生态网络Fig.2 Urban ecology network of large cities

图3 三线城市生态网络Fig.3 Urban ecology network of small and medium－sized cities

从图2，3可以看出，不同类型城市的生态网络图存在差异，相同指标之间在不同类型生态网中的关系不同.

图2显示，二线城市生态网有分割迹象，大致分为3部分，第Ⅰ部分包含9个指标.其中，指标x10，x15，x23，x24和x26突出了日常生活中的社会服务方面，指标x3，x8常识上可以判断为是对自然环境的服务，这一部分反映生态系统的服务水平，可用来描述城市服务系统.第Ⅱ部分包含12个指标，这部分包含指标最多，覆盖面广，可看作整个生态系统的缩影.第Ⅲ部分包含5个指标.这部分指标与居民生活直接相关，代表了居民生活的物质条件.

3部分指标中，Ⅰ，Ⅱ和Ⅲ内部，各指标之间多出现互为影响的现象，而Ⅰ，Ⅱ和Ⅲ各部分之间，则互为影响不显著，说明各部分独立性较强，每个部分内部的指标关系性强.第Ⅰ部分与第Ⅱ部分的关系表现为第Ⅰ部分对第Ⅱ部分只有单向的输出，而第Ⅱ部分没有反馈.如果将指标受到的影响分为2种情况：一种为受城市生态系统内相关指标影响；另一种为受外界系统的影响.则第Ⅰ部分的变动主要受外界系统影响，这一现象说明第Ⅰ部分具有服务的属性.

第Ⅱ，Ⅲ部分间彼此都有输出和输入.第Ⅰ部分与第Ⅲ部分彼此分开，由第Ⅱ部分相连，可以看出第Ⅱ部分所含的指标在二线城市的生态网中的地位更为重要.此外，第Ⅱ部分中，自然和社会2子系统的指标占到了83.33%，说明一个城市要想可持续发展应该将重点放在自然和社会子系统上.

图3给出了三线城市生态网，据图将指标分为2部分，即由14个指标构成的城市生态核心部分和12个指标构成的外围部分.核心部分的指标联系紧密，指标间普遍互为影响.该核心对剩余的12个外围指标多是输出状态，外围指标对核心部分的反馈很少.指标x4，x19，x24对系统内的指标有输出作用，但不受其他指标的影响，说明这3个指标受系统内部的影响很小，被忽略不计，它们的波动主要受外界系统的刺激.

观察以上2个城市生态网，可知部分指标只输入不输出.二线城市中具体表现指标是x2，x7，x20；三线城市中具体表现指标是x7，x25.这些指标都起到汇的作用，可以将它们作为反映指标，用来反映对它们有影响的其他指标的变化.其中需要指出的是，指标x7是第一产业占GDP比例，在2种类型城市中，所有对x7有影响的指标对其都是负作用，且这些指标都归属于社会系统，可以认为在一个城市中，人们的生活水平越高，第一产业在这个城市中所占比例越低.

2 应用与讨论

2.1 城市生态网的定义

城市生态系统是一个复杂的动态系统，各组分通过彼此间的相互联系构成一个复杂的网络.本文根据上述建立的网络图，借鉴食物网、代谢网络、蛋白质相互作用网路、遗传调整网络等一些网的定义及城市生态系统的特点，给出城市生态网定义：在城市生态系统中，根据能量流动、物质代谢、信息流通和人的活动之间的关系，将城市各组分作为节点，用带权重的有向边表示节点之间的联系，最终形成的相互交错，互相联系的网状结构，称为城市生态网.

和众多网络一样，城市生态网也具有复杂网络的特点：结构复杂、网络进化、连接的多样性、动力学复杂性、节点多样性、多重复杂性融合［14］.上述二三线城市生态网又表明它有自身的特点：1）同一时期不同类型城市的城市生态网不同；2）城市生态网是一个含有负权值的复杂网络；3）生态网中2节点间的最优化问题根据实际需要的不同而不同.

2.2 城市生态网的Bacon数

Bacon数是描述复杂网络的一个参数，它描述了网络中任意一个节点到某一特定节点的最短路径［15］.根据中国国内城市现状，依据前图，计算了二、三线城市中每个节点对应的平均Bacon数（AVEB）和最大Bacon数（MAXB），见表1和表2.其中二线城市中的指标x23和三线城市中的指标x16是孤立节点，三线城市中的指标x4，x19，x24不受其他指标影响，这些指标不存在平均Bacon数和最大Bacon数.

表1 二线城市各节点的平均Bacon数和最大Bacon数Tab.1 AVEB and the MAXB of each node in large cities

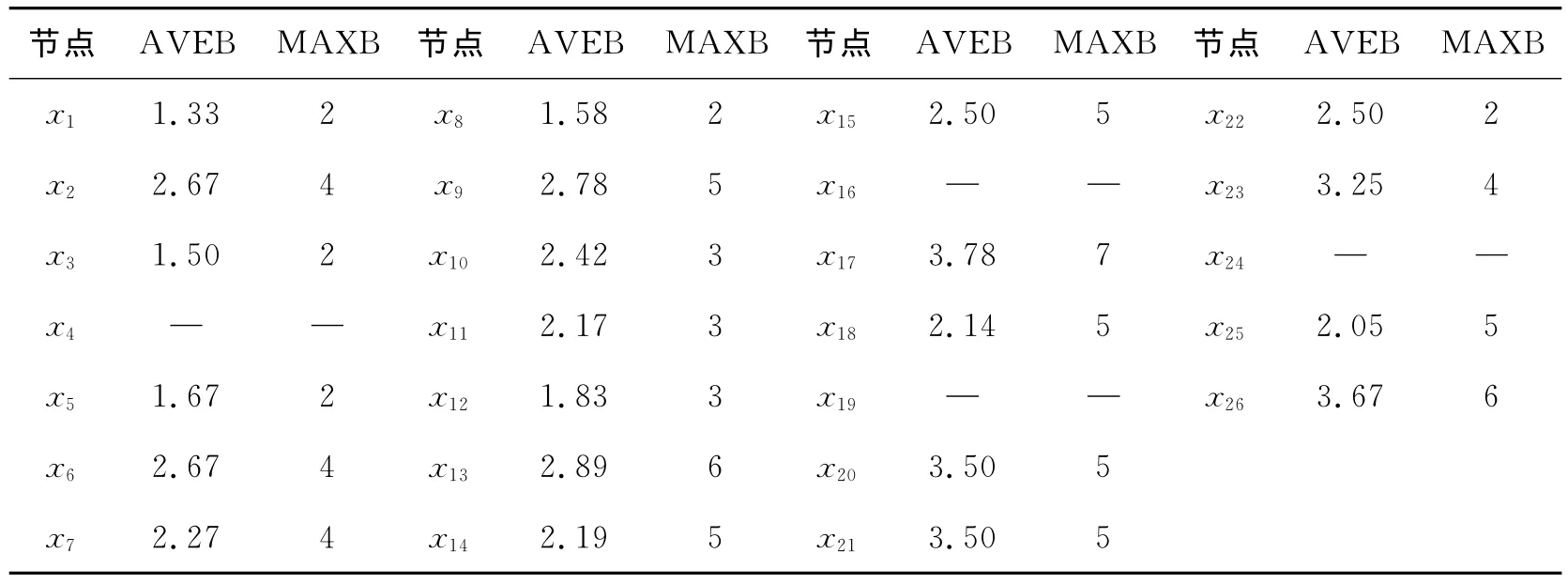
表2 三线城市各节点的平均Bacon数和最大Bacon数Tab.2 AVEB and the MAXB of each node in small and medium－sized cities

表1和表2给出具有可达性2节点之间的最大Bacon数中的最大值是7，平均Bacon数更小，二、三线城市的网络平均Bacon数分别仅为2.76和2.62，因为Bacon数可用来验证小世界理论的正确性，所以城市生态网有可能是一个小世界网络.在节点个数相同的前提下，三线城市的平均Bacon数小于二线城市，这说明三线城市的小世界效应可能更加明显.

2.3 指标之间的最短路径效应

从可达矩阵［16］的性质可知，具有可达关系的指标之间（xi→xj）至少存在1条通路，在这些连接xi，xj的所有路径中，必然有1条最短路径.最短路径本质上可看作一个优化问题，已应用于解决生产实践中的众多问题，如管道铺设［17］、线路安排［18］、厂区选址和布局［19］等，还被用于解决其他最优化问题及预测［20］.在城市生态网中，应用最短路径，对突发状况、人为因素和外界系统干扰引起的城市生态问题，可提供不同的解决方案，使得预期目标达到最优.

2.3.1 最短路径的计算

在城市生态网中，最短路径需要根据实际情况具体分析.本文分2种情况进行了探讨：第1种，从源节点出发，寻找一条到宿节点的路径，使得经过该路径，考虑抑制作用影响力最大的路径.第2种，考虑促进作用影响力最大的路径.在图论应用中，最短路径的权重计算通常采用各边权重求和的方法，考虑到城市生态网和管道、线路等的差异，本文对最短路径计算方法进行了修改，权重值不取各边相加减，而是取各值相乘，即用源节点的变化值依次乘以路径中的权重，最终结果就是源节点对宿节点的影响.

2.3.2 提供方案选择

城市生态系统常常受到外界影响或人为调控，在实践应用中，常常需要根据实际情况选择路径.构建生态网络，可为通路的选择提供不同的方案.例如，在三线城市生态网中，自x8到x18共有5条路（不包括回路路径），分别是①：x8→x14→x18；②：x8→x11→x2→x18；③：x8→x11→x2→x14→x18；④：x8→x11→x6→x2→x18；⑤：x8→x11→x6→x2→x14→x18.计算得到的权重值分别是－0.021 1，－0.037 6，0.037 5，0.036 7和－0.036 7.具体选择通路时，可分为2种情况.

第一，当生态网中某节点受到外界系统影响时，根据影响的性质、大小可进行不同的选择.若使得影响对宿节点产生的干扰达到最小，应选择权重绝对值最小的路径.若想借助影响最大限度地促进发展，应选择权重最大的路径.若想借助影响最大限度地抑制发展，应选择权重最小的路径.例如，假设x8受到外界的冲击而波动，若使x8的波动对x18的影响最小，应选择权重绝对值最小的路径，即路①；若借助x8的波动促进x18的发展，应选择权重最大的路径，即路③；若想借助x8的波动抑制x18的发展，应选择权重最小的路径，即路②.

第二，当人为间接调控生态网中的宿节点时，可通过调节其他节点来达到目的.例如，要改变x18的现状，而又不能对x18进行直接调控，可通过调控x8来影响x18，以达到预期目标.选择好路径后，再通过x18的预期变化量和路径的权重值确定x8的变化量，即人为调控的力度.

具体到本文中，x8是三废综合利用产品产值，x18是人口密度，2节点之间没有任何直接关系，但通过其他节点的连接作用，x8能够影响到x18，其中权值最小的路径为路②，权值最大的路径为路③，二者的区别在于路③中多包含1个节点x14，即建成区面积占市区面积的比例.三废综合利用产品产值增加，工作人员数随之增长，导致产业规模扩大，随之烟尘排放量上升.这时，若增加建成区的面积，以此降低空气中单位体积内烟尘的含量，那么人口会随着建成区面积的扩大而增加.但是，若不增加建成区的面积，单位体积内烟尘含量上升，基于人本能的趋利避害，会外迁去寻找更适宜的居住环境，结果会导致人口密度减少.

2.4 城市生态网中的关键指标

关键节点是指受到攻击后能对网络安全造成重大损失的节点［21］，在不同的网络中，关键节点有不同的应用方式.在生物信息学中，关键节点的识别依据［22－23］是节点的拓扑参数.在无线传感器网络中，关键节点指子网之间信息传输的通道［24］.在城市生态网中，将关键指标选作为关键节点，保证关键节点的稳定就可维护生态网的稳定.

在复杂网络中，可利用重要度评价确定关键节点，该评价方法综合了节点在网络传输中所起的作用、节点度值和相邻节点的重要度贡献［21］，本文利用该方法确定生态网的关键节点.图2中节点x23和图3中节点x16是孤立节点，它们的重要度是0.图2中的节点x2，x7，x20和图3中的x7，x25只输入不输出，这些节点只能被连接，而不能主动连接到其他节点，根据节点效率的含义，它们的重要度是0.二、三线城市生态网中各节点重要度的具体计算结果见表3.

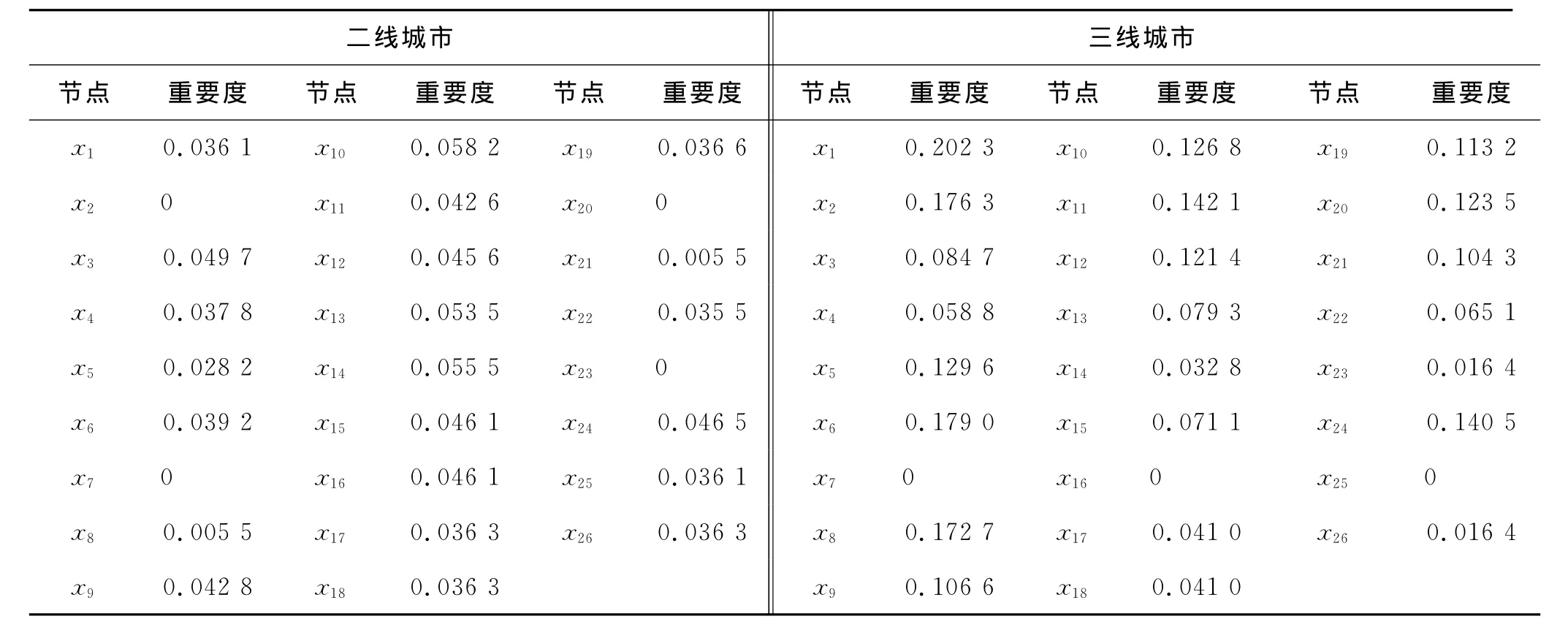
表3 二、三线城市各节点重要度Tab.3 Importance of all nodes in large cities and small and medium－sized cities

从表3中可见，相同节点在不同生态网中的重要性差别很大，例如节点x1，在三线城市中，它的重要度最大，而在二线城市中它的重要度却排到了第17.这说明2类城市发展的侧重点不同，生态网中的关键节点可以反映城市发展的侧重点.

二线城市中重要度最大的节点是第三产业占GDP比例，其次是建成区面积占市区面积的比例，说明二线城市最注重服务业的发展，其次是城市的基础建设.三线城市中重要度最大的节点是工业SO2排放量，然后是工业固废综合利用率，说明三线城市注重环境变化.三线城市中，重要度排前4的节点都与环境有关，表明三线城市对生活环境更加重视.

节点重要度越大说明节点在网络中的地位越关键，关键节点的稳定性直接影响整个城市生态网的稳定，要想维护生态网的稳定，需要尽量保证重要度大的节点的稳定.

3 结论

当前在城市生态系统的研究中，对3大子系统之间关系的研究较少.本文针对3大子系统所含指标之间的相关关系进行了研究，建立了城市生态网，并利用复杂网络理论对城市生态网进行了研究，得到如下结果：

1）利用多元线性逐步回归分析，回归了26个指标之间的关系，通过统计检验，明确确定了指标之间实际的相关关系，并计算了相关指标之间的权重；2）利用图论知识，将选定的26个指标作为节点，构建了城市生态系统网，并探究了城市生态网的定义；3）城市生态网的平均Bacon数表明：中国二、三线城市生态网可能是一个小世界网络；4）在城市生态网中，最短路径的计算不再是单纯的权重最小，而应该是最能满足要求的路径；5）在城市生态网中，可通过节点重要度评价来确定关键节点，从而为维护城市生态网的稳定提供思路，要维护城市生态网的稳定，关键是要确保关键节点的稳定性.

［1］张慧.城市人居环境宜居性评价研究——以临沂市为例［J］.环境科学与技术，2009，32（12）：186－189.ZHANG Hui.Evaluation of city inhabitable environment qualit y taking Linyi as a case［J］.Environmental Science ＆Technology，2009，32（12）：186－189.

［2］胡习英，李海华，陈南祥.城市生态环境评价指标体系与评价模型研究［J］.河南农业大学学报，2006，40（3）：270－273.

HU Xiying，LI Haihua，CHEN Nanxiang.Analysis on indices system and evaluation model of urban ecological environment evaluation［J］.Journal of Henan Agricultural University，2006，40（3）：270－273.

［3］赵延德，张慧，陈兴鹏.城市人居环境质量客观指标评价研究［J］.干旱区资源与环境，2009，23（4）：1－5.

ZHAO Yande，ZHANG Hui，CHEN Xingpeng.Evaluation of city inhabitable environment quality by objective index system［J］.Journal of Arid Land Resources and Environment，2009，23（4）：1－5.

［4］秦伟伟，王卓琳，任文隆，等.生态城市评价指标体系设计［J］.工业技术经济，2007，26（5）：122－124.

QIN Weiwei，WANG Zhuolin，REN Wenlong，et al.Design index system of eco－city assessment［J］.Industrial Technology ＆ Economy，2007，26（5）：122－124.

［5］颜文涛.城市生态系统健康属性综合评价模型及应用研究［J］.系统工程理论与实践，2007，8：137－144.

YAN Wentao.Research on urban ecosystem health attribute synthetic assessment model and application［J］.Systems Engineering－Theory ＆ Practice，2007，8：137－144.

［6］熊鹰，曾光明，董力三，等.城市人居环境与经济协调发展不确定性定量评价——以长沙市为例［J］.地理学报，2007，62（4）：397－405.

XIONG Ying，ZENG Guangming，DONG Lisan，et al.Quantitative evaluation of the uncertainties in the coordinated development of urban human settlement environment and economy：taking Changsha city as an example［J］.Acta Geographica Sinica，2007，62（4）：397－405.

［7］官冬杰，苏维词.城市生态系统健康及其评价指标体系研究［J］.水土保持研究，2006，13（5）：70－73.

GUAN Dongjie，SU Weici.Studies on urban ecosystem health and its assessment indexes system［J］.Research Soil and Water Conservation，2006，13（5）：70－73.

［8］刘香瑞，韩海荣.城市生态系统可持续发展评价研究——以北京市为例［J］.林业资源管理，2006，5：28－33.

LIU Xiangrui，HAN Hairong.Assessment on sustainable development of urban ecosystem：a case study in Beijing city［J］.Forest Resources Management，2006，5：28－33.

［9］苏美荣，杨志峰，陈彬，等.城市生态系统现状评价的生命力指数［J］.生态学报，2008，28（10）：5141－5148.

SU Meirong，YANG Zhifeng，CHEN Bin，et al.The vitality index method for urban ecosystem assessment［J］.Acta Ecologica Sinica，2008，28（10）：5141－5148.

［10］张春泉，马寨璞，佟霁坤，等.城市绿地综合评价研究［J］.河北大学学报：自然科学版，2011，31（1）：85－91.

ZHANG Chunquan，MA Zhaipu，TONG Jikun，et al.General evaluation of urban green space［J］.Journal of Hebei University：Natural Science Edition，2011，31（1）：85－91.

［11］牛凤瑞，白津夫，杨中川.中国中小城市发展报告（2010中小城市绿色发展之路）［M］.北京：社会科学文献出版社，2010：1－26.

［12］王有娟，赵惠云.2009年中国城市统计年鉴［M］.北京：中国统计出版社，2010：43－458.

［13］李云雁，胡传荣.实验设计与数据处理［M］.北京：化学工业出版社，2005：56－59.

［14］何建军.复杂网络节点重要性评价研究［D］.湖南：湖南大学，2010.

HE Jianjun.The evaluation study of node significance in Complex network［D］.Hunan：Hunan University，2010.

［15］汪小帆，李翔，陈关荣.复杂网络理论及其应用［M］.北京：清华大学出版社，2009：9－13.

［16］左孝凌，李为鑑，刘永才.离散数学［M］.上海：上海科学技术文献出版社，2008：287－300.

［17］王彪.基于Dijkstra算法的兰州某区热水管道铺设问题［J］.中国科技博览，2010，14：327.

WANG Biao.The hot water pipe layout problem of a district in Lanzhou based on dijkstra algorithm［J］.China Science and Technology Review，2010，14：327.

［18］李晓东，冯树民.公共交通线路布设方法研究［J］.哈尔滨工业大学学报，2004，36（10）：1365－1367.

LI Xiaodong，FENG Shumin.Method of setting public transport routes［J］.Journal of Harbin Institute of Technology，2004，36（10）：1365－1367.

［19］姬东.图论最短路径问题在消防选址中的应用［J］.武警学院学报，2009，25（12）：10－12.

JI Dong.The application of the shortest path problem of graph theory in fire station distribution［J］.Journal of Chinese People's Armed Police Force Academy，2009，25（12）：10－12.

［20］黄曦，熊慧，邹安全.区域物流网络中多配送中心的库存需求预测模型［J］.工业工程，2011，14（1）：83－86.

HUAGN Xi，XIONG Hui，ZOU Anquan.Prediction model of inventory demand for regional logistics network with multi－distribution centers［J］.Industrial Engineering Journal，2011，14（1）：83－86.

［21］李鹏翔，任玉晴，席酉民.网络节点（集）重要性的一种度量指标［J］.系统工程，2004，22（4）：13－20.

LI Pengxiang，REN Yuqing，XI Youmin.An importance measure of actors（set）within a network［J］.Systems Engineering，2004，22（4）：13－20.

［22］黄海滨，杨路明，王建新，等.基于网络拓扑的生物网络关键节点识别研究进展［J］.数学的实践与认识，2011，41（7）：114－123.

HUANG Haibin，YANG Luming，WANG Jianxin，et al.Identification of essential nodes based on topology of a bionetwork［J］.Mathematics in Practice and Theory，2011，41（7）：114－123.

［23］黄海滨，杨路明，王建新，等.基于复合参数的蛋白质网络关键节点识别技术［J］.自动化学报，2008，34（11）：1388－1359.

HUANG Haibin，YANG Luming，WANG Jianxin，et al.Identification technique of essential nodes in protein networks based on combined parameters［J］.Acta Automatica Sinica，2008，34（11）：1388－1359.

［24］严鸣，汪卫，施伯乐.无线传感器网络中关键节点的节能问题［J］.计算机应用与软件，2007，24（6）：129－131.

YAN Ming，WANG Wei，SHI Bole.Power saving for the articulation nodes in the wireless sensor networks［J］.Computer Applications and Software，2007，24（6）：129－131.