强磁场下熔体中晶粒旋转取向机制及其影响因素

娄长胜，王强，王春江，苑轶，李文，赫冀成

(1.沈阳理工大学材料科学与工程学院，辽宁沈阳110159;2.东北大学 材料电磁过程研究教育部重点实验室，辽宁 沈阳110819)

0 引言

材料中的晶体学取向是一个内禀特性，它对材料的物理性能，尤其是各向异性的力学性能和物理性能有着重要的影响。当多晶体具有宏观上的统一取向后(织构)，材料往往能表现出优异的物理、力学性能[1－3]。因此，控制晶体取向具有重要的研究价值。Mikelson 等[4]观察到均恒磁场具有使合金中的析出相发生取向的现象，认识到磁场能够使具有较强的磁各向异性材料取向的作用，进而初步提出了磁各向异性晶体在均恒磁场中发生旋转取向的理论。随着超导技术在强磁场发生领域的应用，在磁场强度超过2 T 条件下通过熔化法进行的各类材料的晶体(或者第二相)在导电介质中的磁取向实验研究也相继展开[5－7]。

相应地，对金属熔体中的磁致晶体旋转取向的理论研究工作也在实验研究的基础上不断深入。Morikawa 等[8]提出了强磁场下磁取向定性热力学模型。Ferriara 等[9]认为强磁场对高温超导材料织构组织的形成主要是因凝固初始阶段晶粒在熔体中发生旋转而获得的。张邦文等[10]提出了铁磁性物质的旋转取向的动力学模型。Wu 等[11]进行了强磁场下弱磁性物质颗粒的旋转取向机理的分析研究。本文对强磁场下金属熔体中的晶体磁取向的理论进行深入地研究，并对其中的重要影响因素进行具体分析，进而探讨利用强磁场控制熔体中的晶体取向方法。

1 磁场下晶体旋转取向机理

1.1 第二相颗粒发生旋转取向的热力学条件

能量最低原理可理解为体系的能量越低，体系越稳定。磁场下的熔体中体系自由能G 可表示为G=U－TS+pV+ Um.其中:V 为第二项的体积;Um为磁自由能，其大小与体系中物质的磁化强度M 相关，而M 是与具有磁晶各向异性的晶粒取向或与具有形状各向异性的颗粒在空间中的姿态有关。在等温、等压条件下，晶粒的取向或颗粒的姿态不同时，Um也相应地改变。G 的变化ΔG 仅与晶粒的取向或颗粒的姿态有关。熔体中第二相颗粒发生旋转与否，系统获得稳态，取决于不同状态时第二相磁自由能的差异。其根本原因在于磁各向异性，包括磁晶各向异性和形状磁各向异性。

对磁场下晶体旋转取向机制的讨论是基于磁自由能的，弱磁性(|χ|≪1)物质和铁磁性(|χ|≫1)物质的磁自由能[8]分别为

式中:μ0为真空磁导率，取值4π ×10－7H/m;χ 为物质的磁化率;N 为退磁因子;Ho为外加磁场强度;Ms为饱和磁化强度;Hs为饱和磁场强度。

1.1.1 磁晶各向异性晶体的旋转取向机制

在第二相只具有磁晶各向异性特点时，首先讨论弱磁性的情况。为方便起见，假设第二相的晶体类型属于简单结构，并且在不同晶向的磁化率存在如下关系:χc≠χa=χb.根据(1)式，第二相在各方向具有的磁自由能分别为

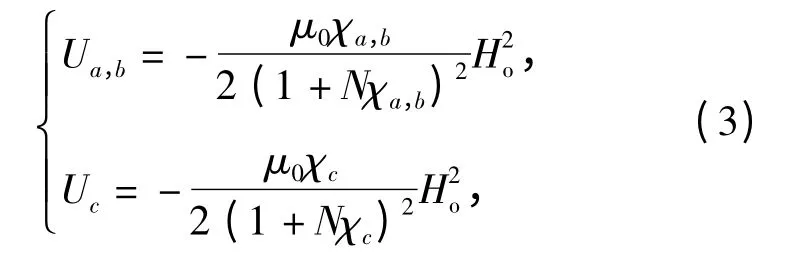
式中:χa，b为a 方向或b 方向的磁化率，χa，b=χa=χb.则第二相在不同晶体方向上的自由能的差异

当χc＜χa，b时，ΔG ＞0，根据能量最低的原则，第二相的c 轴沿垂直于磁场的方向取向;而当χc＞χa=χb时，第二相的c 轴沿平行于磁场的方向取向。将此结论由弱磁性材料推广到铁磁性材料时，亦同样适用。

1.1.2 形状各向异性颗粒的旋转取向机制

当第二相只具有形状磁各向异性特点时，发生旋转取向的热力学条件也要随之改变。由于磁阿基米德效应，第二相周围熔体的影响不容忽视。假设第二相形状为针状或棒状。弱磁性第二相的径向和轴向磁自由能[8]分别为

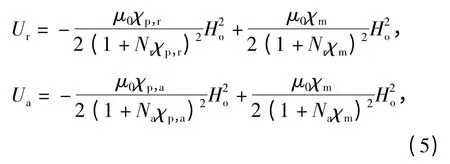
式中:χp和χm分别为第二相颗粒和熔体的磁化率。熔体的磁化率在轴向和径向是一致的。则第二相在轴向和径向的自由能之差ΔG=Ur－Ua表示为

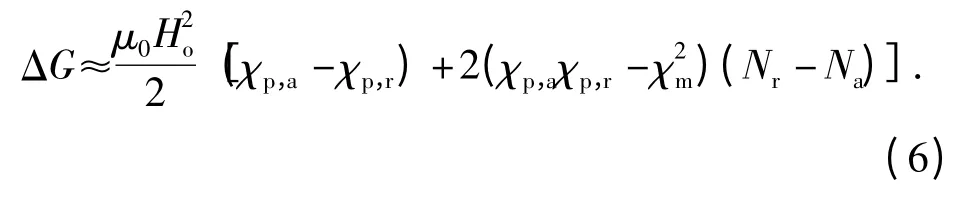
当第二相的磁化率在不同方向差异较小时，即χp，a≈χp，r，(6)式可变为

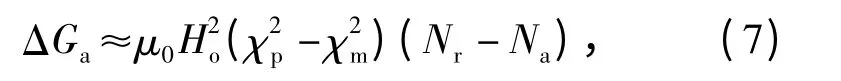
对于针状或棒状，Nr＞Na.因此，当|χp| ＞|χm|时，ΔG ＞0，第二相长轴沿平行于磁场方向取向;当|χp| ＜|χm|时，ΔG ＜0，第二相沿轴向垂直于磁场方向取向。

当第二相和熔体的磁化率差异较小时，即χp，aχp，r≈，(6)式可变为

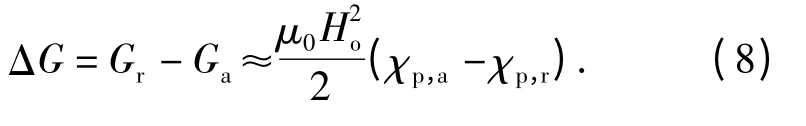
从(8)式可见，当|χp，a| ＞|χp，r|时，ΔG ＞0，第二相轴向沿平行于磁场方向取向;当|χp，a| ＜|χp，r|时，ΔG ＜0，第二相轴向沿垂直于磁场方向取向。

1.2 第二相颗粒在熔体中的动力学运动规律

研究熔体中第二相的取向规律和影响因素，必须从力学的角度入手。众多实验结果[7，12－14]表明，强磁场下金属熔体中的洛仑兹力经常是不可忽视的，在分析中务必考虑洛仑兹力的影响。

强磁场下处于熔体中的第二相的旋转取向行为微观表现为第二相受到磁力矩的作用，为了简化问题和方便讨论，假设:1)第二相为弱磁性物质，其具有磁各向异性，易磁化轴的磁化率为χe，难磁化轴的磁化率为χd;2)以第二相的易磁化轴和难磁化轴为坐标轴建立迪卡尔直角坐标系，并设定易磁化轴和外加磁场B 的夹角为θ.

当磁化强度矢量与磁场矢量不平行的时候，第二相会受到的磁力矩

式中:Δχ=χe－χd;V 为第二相的体积;r 为第二相为球体时的半径。第二相转动过程中会受到粘性阻力的作用，其转矩为

式中:η0为熔体的粘度;负号表示粘性阻力产生的转矩与转动方向(dθ/dt)相反。

液态金属熔体大多导电，第二相颗粒在其中运动时，会带动周围的熔体运动，产生感生涡流，进而产生洛仑兹力[13]。由洛仑兹力引起的转矩也将阻碍颗粒的转动，建立如图1 所示的坐标系进行分析。磁场方向平行于x 轴，第二相的空间位置为(r，φ，θ)，能够在xOy 平面自由旋转。设第二相转动的速度和转动半径分别为

图1 晶体取向空间坐标系Fig.1 Space coordinates system of magnetic orientation

在近似认为第二相的转动速度引起熔体以相同的速度流动时，其产生的洛仑兹力引起的转矩为

式中:ix、iy、iz分别为x、y、z 方向上的单位矢量;σm为导电熔体的电导率。考虑到第二相的体积，洛仑兹力产生的转矩Tl为(13)式在第二相体积上的积分

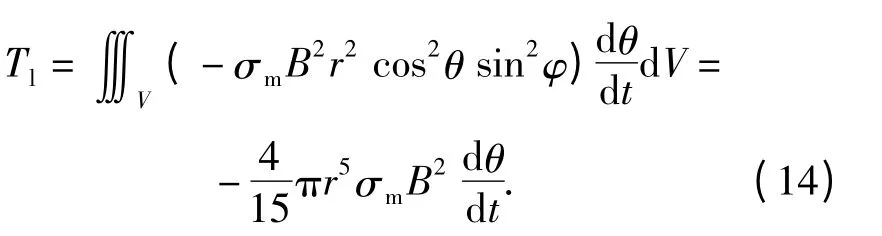
根据经典牛顿力学，第二相的运动可以通过(15)式来描述:

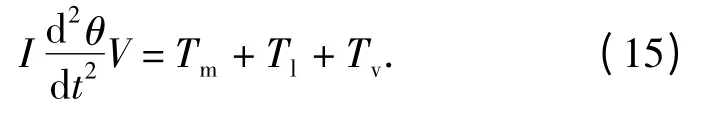
在转动过程，第二相在初始时刻的加速过程短暂地几乎可以忽略[10]。因此，可以近似认为转动过程始终处于平衡状态，即将Tm、Tl、Tv代入(15)式中，可求得转动角速度

(16)式中的物理参数取值如下:Δχ =10－5，B =3 ～10 T，r 为10－6～10－5m，σm为107～108Ω－1·m－1，η0=10－3Pa·s，ω 约在1 ～105rad/s 的范围内。可看出，强磁场下的熔体中晶体取向过程非常迅速，一般在数秒的时间即可完成。其解为

式中:θ0为初始时刻易磁化轴与磁场方向的夹角;为特征时间。取向过程的θ－t关系曲线如图2 所示。

图2 易磁化轴与磁场方向的夹角与取向时间关系图Fig.2 Time－dependent angle between easy magnetization axis and the direction of magnetic field under various magnetic field conditions

由图2 可看出，当特征时间τ 相同时，易磁化轴与磁场方向的初始角θ0越小，完成取向的时间越短;当初始角θ0相同时，特征时间τ 越小取向进程越快。

2 磁场下影响晶体取向的因素

在上述磁致旋转取向机制的推导过程中，没有考虑其他任何外部因素的影响，如体系温度、重力场和第二相自身的形状等。因此利用上述过程在分析实际问题的时候可能会出现与现象偏离的情况。下面对强磁场下晶体取向有较大影响的3 个因素分别进行分析。

2.1 温度的影响

体系的温度对晶体取向的影响表现为分子热运动(旋转布朗运动)对晶体取向的扰动。对于熔体中微小的球状第二相，分子热运动造成第二相做无规律的旋转布朗运动，运动的驰豫时间可表达为

式中:η0为导电熔体的粘滞系数;k 为波尔兹曼常数，k=1.38 ×10－23J/K.温度越高，τB越短，表明第二相在高温熔体中的布朗运动愈剧烈。而利用强磁场取向必须克服旋转布朗运动的扰动，即磁场的取向时间必须小于τB.磁场的取向时间可用(17)式中的特征时间τ 来近似取代。因此τ 和τB的关系可表示为

在绝大多数的取向体系中，30η0≫σmr2B2总是成立的。因此当哈特曼数Ha≪1 或Ha≈1 成立时，(19)式可简化为

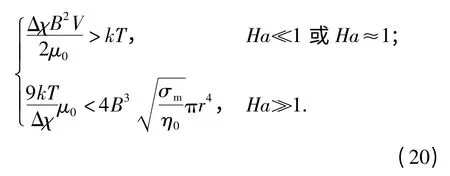
(20)式可反映温度对第二相晶体取向的影响规律，如图3 所示，图中阴影区域为对应磁场下第二相不能发生取向的尺寸范围。根据(19)式或图3能够确定晶体取向所需的最小磁场强度，或确定晶体取向所要求的最小尺寸rmin.因此，温度对第二相取向的影响实质是对第二相体积的选择。当T =1 000 K，B=5 T，Δχ=10－5时，磁致旋转取向的rmin≈50 nm.

图3 由温度决定的第二相取向范围Fig.3 Temperature－dependent orientation of the second phase

2.2 重力的影响

当第二相体积较大时，重力会引起第二相在熔体中迁移。在有限的空间内，迁移会在一定的时间内完成，因此取向时间应小于迁移时间。设空间中迁移的长度为l，颗粒的迁移速度为vt，则迁移时间τg=l/vt.第二相的取向时间取(17)式中的特征时间τ.取向时间与迁移时间具有下列关系:

式中:F 为颗粒在重力方向上所受的阿基米德合力。尺寸较大的第二相在强磁场下一般有30η0≪σmr2B2，因此，(21)式可简化为

(22)式决定了能够发生磁取向的第二相的尺寸最大值rmax，其值与B1/3呈正比。图4 给出了根据(22)式第二相尺寸与磁场强度的关系，图中阴影区为第二相能够在重力场中取向的尺寸范围。当第二相所受到的阿基米德合力F 在103～105N/m3的范围变化时，磁取向的最大半径一般稳定在数毫米。

对于尺寸较小的第二相，在较弱磁场条件下一般会有30η0≫σmr2B2，此时Ha≪1 或Ha≈1 成立，(22)式可简化为

可看出，当第二相较小、磁场较弱时，第二相的最大尺寸与磁场强度B 呈线性关系。取l=0.01 m，η0=10－3Pa·s，σm=108Ω－1·m－1，Δχ =10－5时，二者的关系图显示为图4 中磁场强度较低时的曲线。

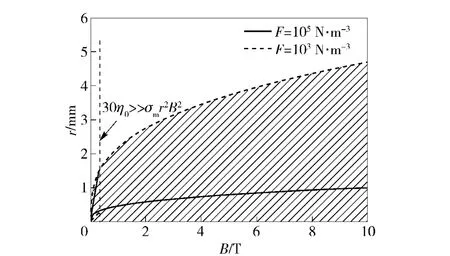
图4 由重力决定的第二相取向范围Fig.4 Gravitational force－dependent orientation of the second phase

2.3 第二相形状的影响

实际熔体中第二相常见棒状、针状、块状、层片状等形状。不同形状的第二相所受的力矩也不同，进而影响其运动。以棒状为例，分析第二相形状对其取向的影响效果。

设棒状第二相的直径为d，长度为l'.以第二相的轴向和径向为坐标轴建立迪卡尔直角坐标系，并设轴向和磁场的夹角为α，棒状第二相轴向的磁化率为χ'a，径向的磁化率为χ'r.如图5 所示。

在上述坐标系下，第二相所受到的磁力矩为:

粘性阻力和洛仑兹力产生的力矩分别表示为

因此，在平衡时有

对比(27)式和(17)式可知，强磁场下第二相的形状不会对其取向带来本质的影响。

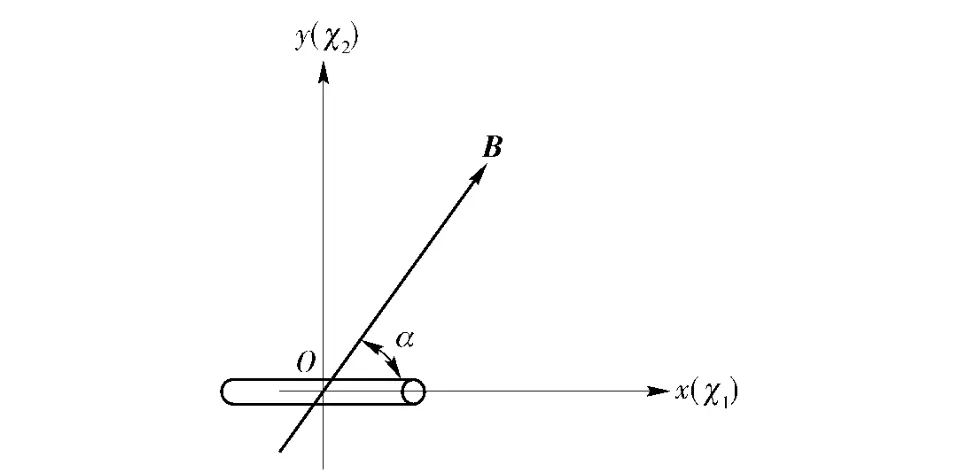
图5 磁场下第二相受力分析坐标系Fig.5 Coordinate system for the force analysis of the second phase in magnetic field

3 试验验证

3.1 熔体中第二相旋转取向的试验

不同磁性的物质在熔体中，由于磁晶各向异性或形状各向异性导致的晶粒取向和颗粒排列，已在试验中得到了验证。例如，Al－6.8 Ni 合金中弱磁性的Al3Ni 析出相在有无磁场时XRD 分析结果如图6所示[7]。由图6 可明显看出，施加外场后Al3Ni 相的(hk0)晶面衍射峰的增强，表明c 轴平行于磁场方向。对比未施加磁场时的结果，可判定Al3Ni 相在外加磁场的作用下，发生了旋转。

图6 Al－6.8 Ni 合金中Al3Ni 相有无磁场下的XRD 谱图Fig.6 XRD patterns of Al3Ni phase in parallel section of Al－6.8 Ni with and without strong magnetic field

形状各向异性导致的第二相颗粒旋转取向也在添加过量TiAl3颗粒的Al－Si 合金的凝固试验中发现[12]:针状或棒状的TiAl3颗粒在无磁场时是随机排列的;而在11.5 T 强磁场条件下凝固样品中颗粒平行于外加磁场方向排列，如图7 所示。由于TiAl3熔点远较Al 合金高，在熔体中会保留固态长颗粒状。在外加强磁场的作用下，长轴方向趋于外场方向运动以减小自由能，达到稳定状态。

图7 Al－Si 合金凝固组织中外加TiAl3颗粒在有无磁场条件下的排列Fig.7 The alignment of TiAl3 particles in Al－Si solidified structures with and without high magnetic field

3.2 重力场下的熔体中第二相旋转取向试验

如前所述，第二相在熔体中发生旋转获得取向组织时会受到诸如温度、重力等其他因素的影响。因此，在实际利用强磁场控制获得有取向的凝固组织试验中，务必要考虑这些因素。

重力场对凝固组织的影响比较大，它会导致第二相因密度与熔体不同造成的重力偏析现象。文献[12]的研究中发现，TiAl3会在重力的影响下发生沉降行为。在施加11.5 T 磁场的条件下，TiAl3颗粒在沉降过程中即完成了旋转，形成了颗粒取向排列的凝固组织，颗粒的长轴方向平行于外加磁场方向。此外，有无磁场下Bi－4.36 Mn 合金半固态凝固试验研究中发现[15]，相对无磁场下的晶粒随机取向，11.5 T 磁场下的凝固组织中MnBi 晶粒的长轴平行于磁场方向，如图8 所示。XRD 分析则显示了MnBi相的易磁化c 轴平行于施加的外磁场方向，如图9所示。试验结果表明，尺寸合适的MnBi 晶粒能在发生沉降行为前完成旋转取向，并继续长大，形成长轴(c 轴)平行外加磁场方向的组织。

上述试验的结果验证了在重力场下利用强磁场对熔体中第二相的旋转取向具有控制作用。可利用物质内禀磁性的差异，通过选择合适的第二相物质、改变体系的温度及控制熔体中第二相尺寸等方法，在强磁场下制备出具有取向一致的金属基复合材料。

图8 Bi－4.36 Mn 合金在有无磁场下的凝固组织Fig.8 Microstructures of Bi－4.36 Mn alloys solidified in 0 T and 11.5 T magneticfields

图9 Bi－4.36 Mn 合金在有无磁场下的XRD 谱图Fig.9 XRD patterns of Bi－4.36 Mn alloys solidified in 0 T and 11.5 T magneticfields

4 结论

强磁场下，金属熔体中的第二相晶粒会发生旋转取向。本文对发生取向的热力学判据和运动过程规律进行了系统的理论分析，得到以下结论:

1)强磁场下，熔体中第二相取向的主要原因是体系发生旋转，体系自由能降低。其主要决定于因磁各向异性引起的、在空间不同方向存在差异的磁自由能。

2)强磁场下，熔体中第二相旋转运动是作用于第二相上的合力矩的结果。晶粒的初始状态和特征时间决定了进程的快慢。

3)除第二相和磁场的物性外，其他因素也对晶体旋转取向有较大影响。体系温度要求第二相发生旋转取向时的最小尺寸临界值;而重力的影响决定了第二相尺寸的最大临界值;第二相形状对其取向的规律没有大的影响，只影响取向的时间。

4)可通过选择合适的第二相物质、改变体系的温度及控制熔体中第二相尺寸等方法，在强磁场下制备出具有取向一致的金属基复合材料。

References)

[1]杨勇彪，王富耻，谭成文，等.不同取样方向AZ31B 镁合金应变率效应[J].兵工学报，2008，29(11):1347 －1351.YANG Yong－biao，WANG Fu－chi，TAN Cheng－wen，et al.Research on strain rate effects of AZ31B magnesium alloy of different orientation samples[J].Acta Armamentarii，2008，29(11):1347－1351.(in Chinese)

[2]Du X H，Wang Q M，Belegundu U，et al.Crystal orientation dependence of piezoelectric properties of single crystal barium titanate[J].Materials Letters，1999，40(3):109 －113.

[3]李英雷，胡时胜，魏志刚，等.大变形锻造钨合金动态力学性能研究[J].兵工学报，2003，24(3):378 －380.LI Ying－lei，HU Shi－sheng，WEI Zhi－Gang，et al.Dynamic behaviour of tungsten alloy forged with lage formation[J].Acta Armamentarii，2003，24(3):378 －380.(in Chinese)

[4]Mikelson A E，Karklin Y K.Control of crystallization processes by means of magnetic fields[J].Journal of Crystal Growth，1981，52(2):524 －529.

[5]Fujiwara M，Fukui M，Tanimoto Y.Magnetic orientation of benzophenone crystals in fields up to 80.0 kOe[J].The Journal of Physical Chemistry B，1999，103(14):2627 －2630.

[6]Sazaki G，Yoshida E，Komatsu H，et al.Effects of a magnetic field on the nucleation and growth of protein crystals[J].Journal of Crystal Growth，1997，173(1):231 －234.

[7]Wang C J，Wang Q，Wang Z Y，et al.Phase alignment and crystal orientation of Al3Ni in Al–Ni alloy by imposition of a uniform high magnetic field[J].Journal of Crystal Growth，2008，310(6):1256 －1263.

[8]Morikawa H，Sassa K，Asai S.Control of precipitating phase alignment and crystal orientation by imposition of a high magnetic field[J].Materials Transactions JIM，1998，39(8):814 －818.

[9]Ferreira P J，Liu H B，Vander Sande J B.A model for the texture development of high－Tc superconductors under an elevated magnetic field[J].Journal of Materials Research，1999，14(7):2751－2763.

[10]张邦文，任忠鸣，王晖，等.合金凝固过程中晶粒磁取向的动力学研究[J].金属学报，2004，40(6):604 －608.ZHANG Bang－wen，REN Zhong－ming，WANG Hui，et al.On dynamics of grains alignment during alloy solidification under applied of magnetic field[J].Acta Metallurgica Sinica，2004，40(6):604 －608.(in Chinese)

[11]Wu C Y，Li S Q，Sassa K，et al.Theoretical analysis on crystal alignment of feeble magnetic materials under high magnetic field[J].Materials Transctions JIM，2005，46(6):1311 －1317.

[12]Lou C S，Wang Q，Wang C J，et al.Migration and rotation of TiAl3particles in an Al－melt solidified under high magnetic field conditions[J].Journal of Alloy and Compouds，2009，472(1):225 －229.

[13]Yasuda H，Ohnakai I，Kawakami O，et al.Effect of magnetic field on solidification in Cu－Pb monotectic alloys[J].ISIJ International，2003，43(6):942 －949.

[14]晋芳伟，任忠鸣，任维丽，等.强梯度磁场下金属熔体中析出相晶粒迁移的动力学研究[J].物理学报，2007，56(7):3851 －3860.JIN Fang－wei，REN Zhong－ming，REN Wei－li，et al.On dynamics of precipitated grains migrating in molten metal under high gradient magnetic field [J].Acta Physica Sinica，2007，56(7):3851 －3860.(in Chinese)

[15]Lou C S，Wang Q，Liu T，et al.Effects of a high magnetic field on the coarsening of MnBi grains solidified from isothermal annealed semi－solid melt[J].Journal of Alloys and Compouds，2010，505(1):96 －100.