基于改进两相流模型的模块装药内弹道模拟

马昌军，张小兵

(南京理工大学 能源与动力工程学院，江苏 南京210094)

0 引言

模块装药是为提高大口径火炮反应能力，实现自动装填而出现的新型发射装药技术。传统布包式装药和人工装填效率太低，模块装药配合自动装填系统可使火炮射速提高1 倍以上。同时，模块装药的运输、储存更加方便和安全，故其已成为未来先进火炮的发展趋势。

这种装药结构可能会使内弹道性能变差，膛内压力波增大，降低发射安全性。梁世超等[1]比较了模块装药、药包装药及不同传火结构的弹道性能，发现模块装药会给弹道安全性带来困难。余斌[2]对模块装药点传火进行了研究，得出模块装药传火较慢且有延时。赵毅[3]认为模块装药不可避免地造成局部点火。王育维等[4]得出小号装药压力波更严重。

模块装药的数值模拟建立在对膛内分区基础之上。该方法可追溯到1992 年Briand 等[5]对模块装药火炮内弹道早期膛内过程进行模化，分为5 个区。但仅对点传火的过程进行了模拟，不涉及模块的破裂和弹丸的运动。为考虑整个内弹道过程，研究者根据模块是否破裂将膛内过程分为2 个阶段分别进行分区。分阶段分区建模的方法假设模块同时破裂，但Légeret 等[6]对模块装药点火过程进行计算和实验得出模块在膛内不是同时破裂的。国内陆中兵等[7]模拟了短管炮模块装药膛内两相流、模块两端隔板开有圆孔等的模块装药内弹道过程。

由于模块装药的结构复杂性，使得建模和模拟计算难以精确地符合真实情况。本文提出了对模块装药内弹道模型的改进方法，试图更准确地反映模块装药的特点以及对模块装药性能的影响。

1 模块装药内弹道物理过程及数学模型改进

1.1 模块装药内弹道物理过程及假设条件

模块装药结构如图1 所示，装药由一个或多个模块组合而成，各模块盒大小相等，装填时位置可互换。每个模块包含盒体、中心传火管、传火管端盖等，模块是全可燃的。模块盒体密闭，内装主发射药，中心传火管内是黑火药，点火管两端是用于密封与防潮的端盖。

模块装药内弹道物理过程可概括为:火炮击发点燃膛底模块的中心传火管，火焰在该点火管内传播。此时，各模块内主装药及后续模块的中心传火管仍是密封的。模块间传火的条件是压力达到传火管端盖的破孔压力导致端盖破裂。随着传火管内火药燃烧，压力上升。当压力达到一定值时，端盖破裂，火药燃气及少量黑火药颗粒从点火管两端流出，火焰向后续模块传播。在此过程中，若压力达到传火孔破孔压力，火药燃气将逐步加热并点燃主装药，模块内压力上升。模块内外压差达到一定值的时候，模块盒体破裂，模块内未燃完主装药散落到药室自由空间内。当模块全部破裂，所有未燃完火药分散在药室自由空间内燃烧至全部燃完，弹丸出炮口，内弹道过程结束。

图1 模块装药的发射药盒Fig.1 Cartridge cases of modular charge system

为了用数学模型描述上述过程，对实际过程进行假设如下:

1)中心传火管端盖破裂前，点火管和模块体保持密闭且能承受一定压力;

2)传火孔未破孔且模块盒未破裂时，模块保持密闭;

3)传火管破孔后，传火管和对应模块有气、固两相流动。传火管端盖破裂后，考虑传火管之间的两相质量、动量和能量交换;

4)全装药因惯性大、药室内自由空间小，忽略模块的运动;

5)火药按几何燃烧规律燃烧，不考虑火药颗粒的破碎与变形;气相服从诺贝尔－阿贝尔方程。

1.2 两相流模型针对模块装药的改进

1.2.1 改进的模块装药两相流模型

根据模块装药的特点和上述假设，对已有的两相流模型进行改进。

1)各模块和传火管单独建模

首先，由于装药的不连续，模块破裂前气、固两相运动都局限在模块内部;其次，各中心点火管之间被端盖阻隔，点火过程也是不连续的。因此，改进的模型对各模块和传火管采用独立的两相流方程组来描述，破裂前没有质量或能量交换。传火管端盖破裂后，相邻传火管产生质量、动量和能量交换。

2)考虑模块的分别破裂

数值模拟和实验研究均发现模块是非同时的破裂。本文所建立的改进模型考虑模块的分时破裂，模块破裂时点火管也同时破裂，点火管内未燃烧完点火药同时融合进入主装药床进行计算。

3)模块破裂准则

采用压差作为模块的破裂准则，模块破裂主要是由盒体内外压力差引起的。实际使用的模块药盒是密闭的，且满足一定耐压强度和力学性能。模块在破裂前保持密闭，不考虑透过模块壁的流进流出。

模块内压力值取决于流入的源项和主装药燃烧释放燃气，其中流入质量源项可用(1)式计算:

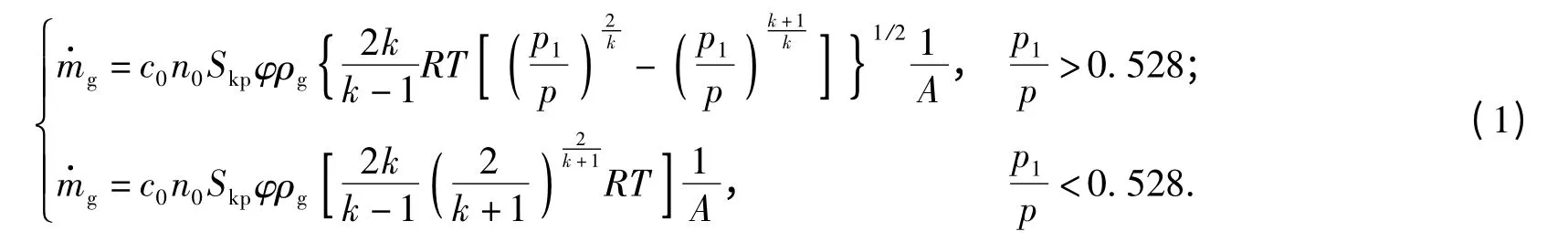
式中:c0为流量系数;n0为单位长度下的小孔数目;Skp为小孔面积;φ 为空隙率;ρg为气相密度;k 为比热比;R 为气体常数;T 为气相温度;p1为模块内压力;p 为点火管内压力;A 为截面积。

模块无破裂时，外部压力取决于点火管释放的气体源项，使用(1)式的流量方程得到气体质量，再结合状态方程可求得外部压力。有模块破裂后，外部压力应该由破裂融合后的装药床的压力分布得到。

根据上述假设建立如下数学模型:模块破裂前，膛内每个模块和其对应的中心传火管使用1 组耦合双一维两相流方程描述。模块破裂后，盒内未燃完主装药、传火管内黑火药及气相产物融合到膛底至未破裂模块间的自由空间，形成主装药床，使用1 组新的两相流方程描述。随着模块破裂，主装药床不断扩展，至所有模块破裂。弹丸达到启动压力后开始运动，直到弹丸出炮口内弹道过程结束。

1.2.2 模块装药耦合两相流方程及辅助方程

内弹道两相流方程组包含气相连续方程、气相动量方程、气相能量方程、固相连续性方程、固相动量方程，模块主装药区两相流方程如下:

1)气相连续方程

式中:t 为时间;x 为一维位移变量;A 为模块盒体内径截面积;ug为气相速度;为火药燃烧生成的气体流量;为从点火孔流入的气体流量。

2)气相动量方程

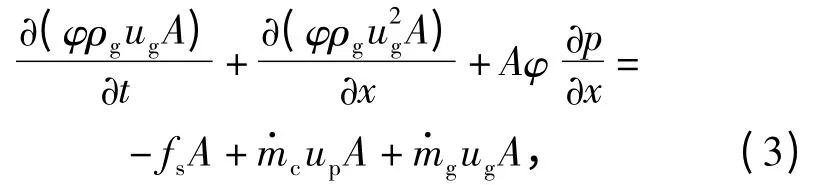
式中:fs为相间阻力;up为颗粒相速度。

3)气相能量方程

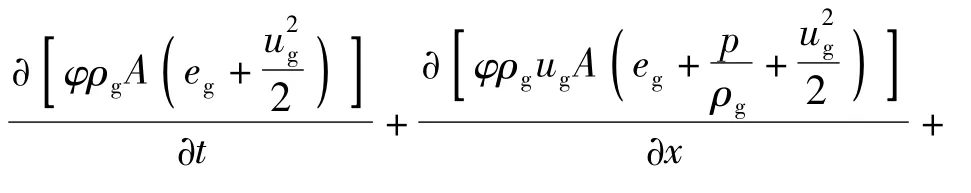
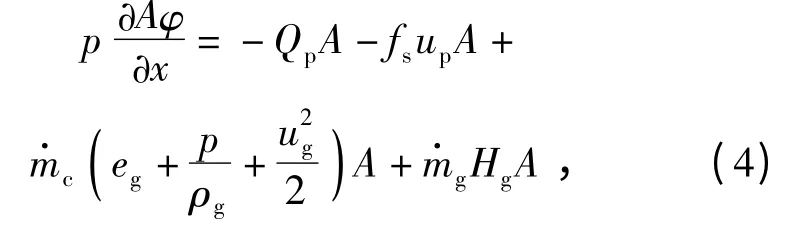
式中:eg为火药化学潜能;Qp为相间传热相;Hg为气相流入量的焓。

4)固相连续性方程

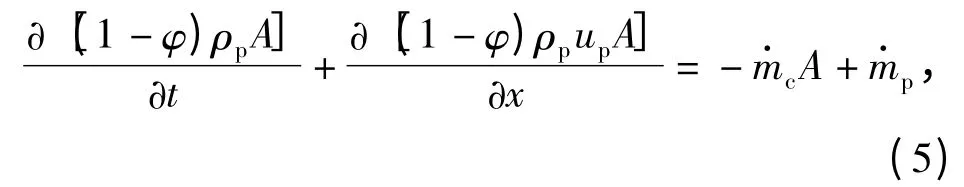
式中:ρp为火药密度为点火孔的固相流入量。

5)固相动量方程

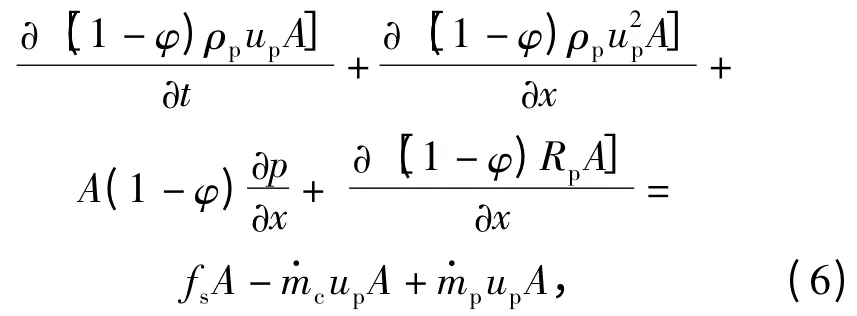
式中Rp为颗粒间应力。

点火管与模块内两相流方程类似，只是截面积、火药参数不同，源项部分对于主装药为流入而对于点火管是流出，在相应地方修改即可得到。为使方程封闭，需要一系列辅助方程，包括状态方程、颗粒间应力、相间阻力、相间传热、颗粒表面温度、燃烧规律以及流量计算公式等参见文献[8].

1.2.3 模块破裂后主装药床融合准则

模块破裂时，盒体与传火管同时破裂。破裂后，未燃完的黑火药和主装药融合到一起，分散在膛内自由空间。以气相质量守恒为例:将破裂前点火管和模块盒内对应网格单位长度的气相质量相加得到融合后总气相质量。将总气相质量按照网格长度分配到新划分的主装药床，即可得到融合后药床的初始分布。融合后气相质量

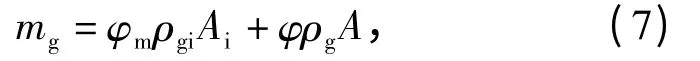
式中:φi为点火管内空隙率;ρgi为点火管内气相密度;Ai为点火管截面积。

同样，可得到气相动量、气相能量、固相质量和固相动量分布。方程结合状态方程，求得融合后空隙率、速度、气相密度、气相温度及压力等参量。

1.2.4 初边值条件

以某155 mm 榴弹炮模块装药为例进行求解，装药质量15.5 kg，发射普通榴弹，弹质量45 kg.

传火管破孔、端盖破裂及模块破裂均使用压力准则，破孔压力20 MPa，端盖及模块盒体破裂压力与材料及膛内燃烧情况有关。点火管破孔、端盖破裂及模块破裂均使用耦合边界处的压力差作为破裂条件。点火管破孔采用模块内压力和管内压力差作为判断条件，模块间传火采用相邻传火管端盖两侧的压力差作为判断条件，而模块破裂则采用模块内压力和空隙区的压力差作为判断准则。

开始时，模块及中心传火管均为固壁边界，采用镜面反射法。模块破裂后，按照融合准则形成新的主装药床，未破裂模块仍为固壁边界不受影响。

2 模拟结果

根据所建立的改进模块装药内弹道两相流数学模型，采用Mac－Cormack 格式求解，所得结果如图2 ～图12 所示。图2 为膛底压力随时间变化曲线，图3为弹丸运动速度变化曲线，图4 为压力波曲线。数值计算结果与实验数据对比如表1 所示。

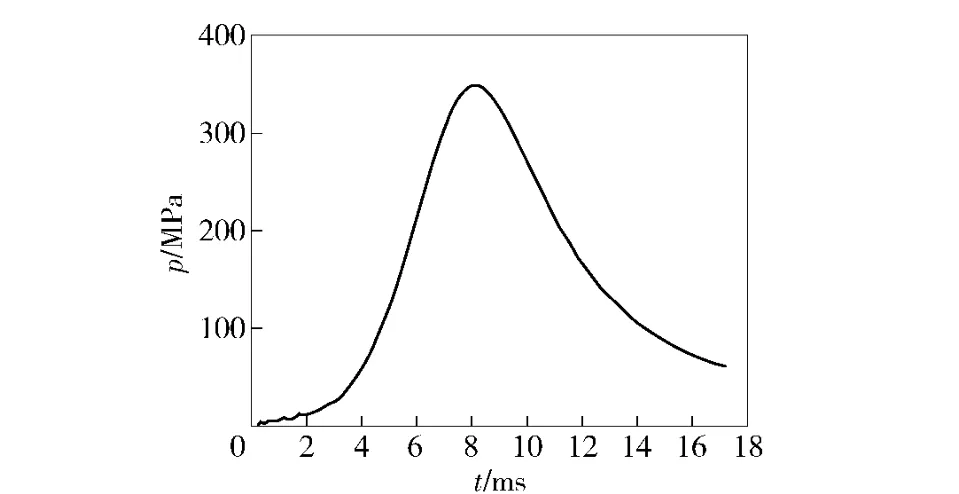
图2 膛底压力时间曲线Fig.2 Pressure－time curve at the end of chamber

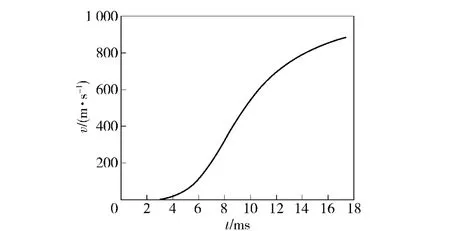
图3 弹丸速度时间曲线Fig.3 Velocity－time curve of the projectile

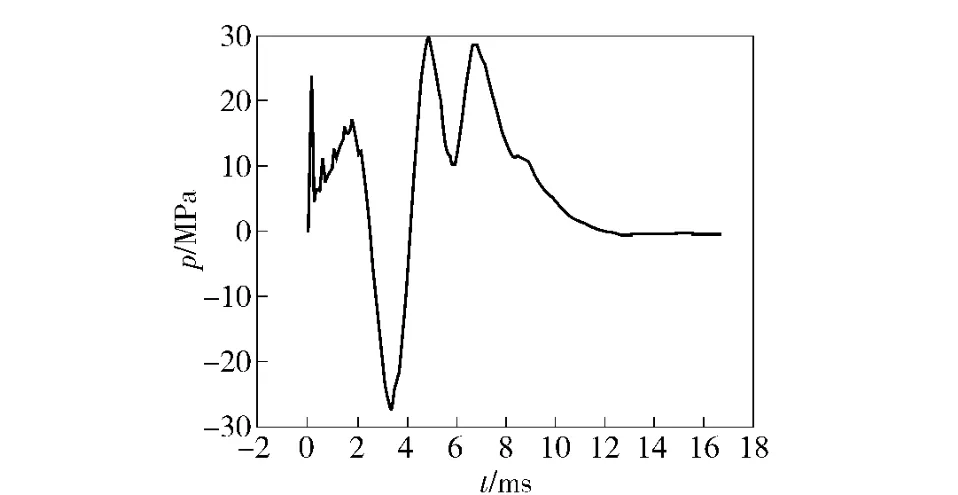
图4 压力波变化曲线Fig.4 Change curve of pressure wave

表1 模拟数据与实验数据[9]对比Tab.1 Comparison of the simulated and experimental results

由图2、图3 和表1 可见，数值模拟的结果和实验测得结果比较接近。由图4 可知，模块装药膛内的压力波变化范围较大，第1 个负压差接近30 MPa，开始时刻的压差快速上升是由于点火管内的黑火药快速燃烧向膛底空隙区流动引起的。

如图5 所示位于膛底的1 号模块中心传火管内气相速度分布。图6 和图7 分别为1 号模块破裂前的压力及空隙率分布。

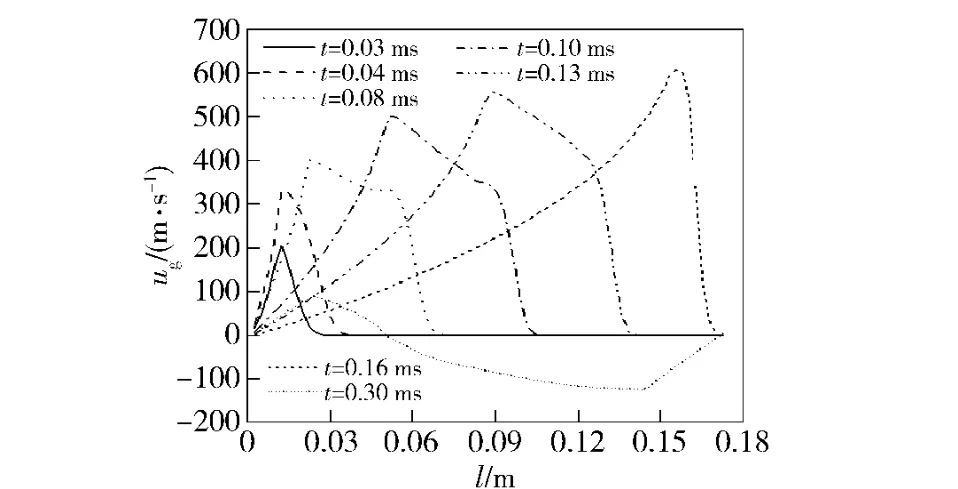
图5 模块1 中心点火管内气相速度分布Fig.5 Velocity distribution of gas phase in ignition tube

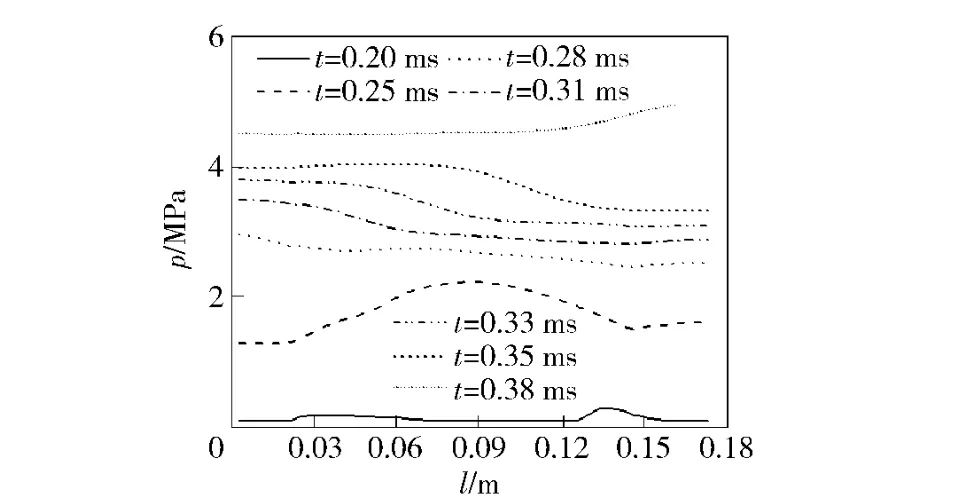
图6 模块破裂前模块1 内压力分布Fig.6 Pressure distribution in modular case 1 before rupturing

由图5 可看出，点火管内气流逐渐向弹底方向传播。当压力波动传播到传火管另一端时，由于端盖未破裂，产生了压力波的反射，气流方向改变。

由图6 可看出，模块内压力从中间开始上升，由于模块中心传火管是从中间开始破裂的。

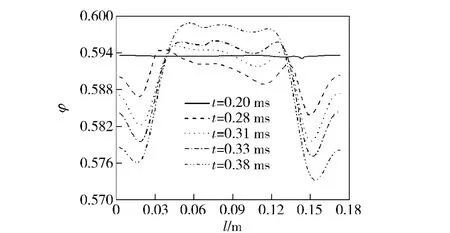
图7 模块破裂前模块1 内主装药空隙率分布Fig.7 Porosity distribution in modular case 1 before rupturing

由图7 可看出，模块内的空隙率呈现中间高两端低的形式，由于初始时模块内压力中间高两端低，故气固两相从中间向两端流动。

图8 和图9 分别为模块内压力和弹后空间空隙率分布曲线。如图8 所示，内弹道开始至1、2 两模块着火，而其余模块未着火时的压力分布。可看出模块破裂前，各模块内的压力变化相互独立，模块保持密闭。

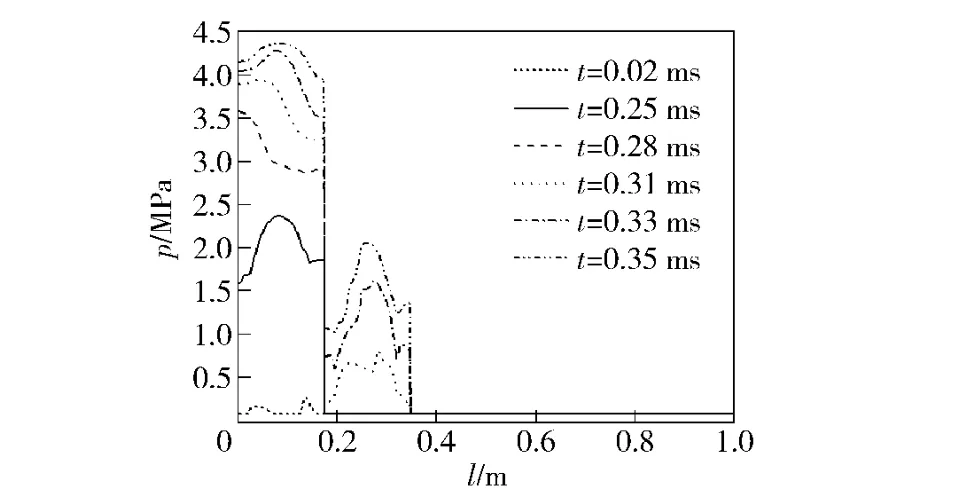
图8 内弹道初期不同时刻各模块内压力分布Fig.8 Pressure distribution in each modular case

如图9 所示不同时刻主装药床的空隙率分布曲线。可看出，膛内空隙率存在不连续。由于颗粒相的运动滞后于气相流动，膛内空隙率间断不能在短时间内抹平，而是逐渐变化。t=5.59 ms 时，弹丸运动后，颗粒运动滞后于火药燃气流动，弹后的空隙率迅速增大并接近1.

由膛内压力分布可看出弹丸开始运动时，膛内压力梯度较大;随着弹丸的运动压力分布趋向平缓。

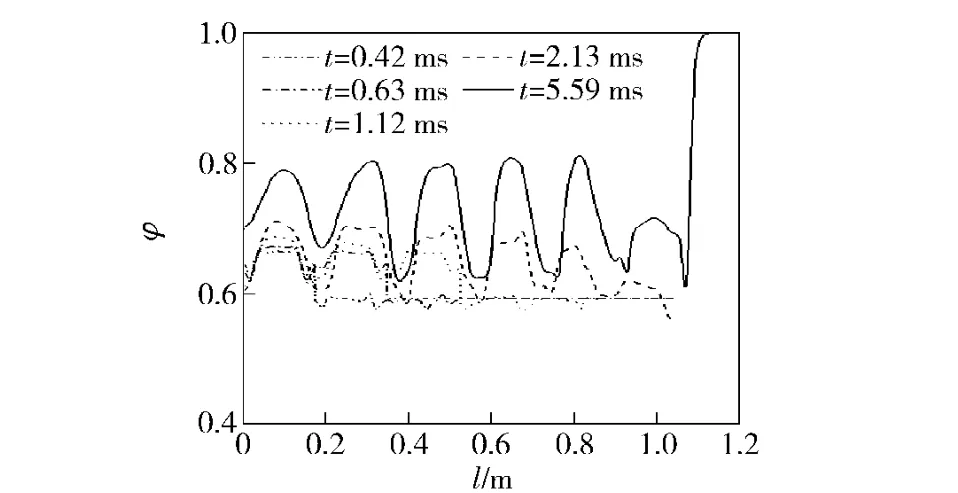
图9 不同时刻空隙率分布曲线Fig.9 Porosity distribution at different time

表2 为不同中心传火管端盖强度对主装药点火时间的影响，图10 为模块开始破裂时间随模块强度的变化，图11 为端盖强度对模块破裂时间的影响。

表2 主装药全面着火时间随中心传火管端盖强度变化关系Tab.2 The effect of different strength of tube cap on the ignition time of main charge

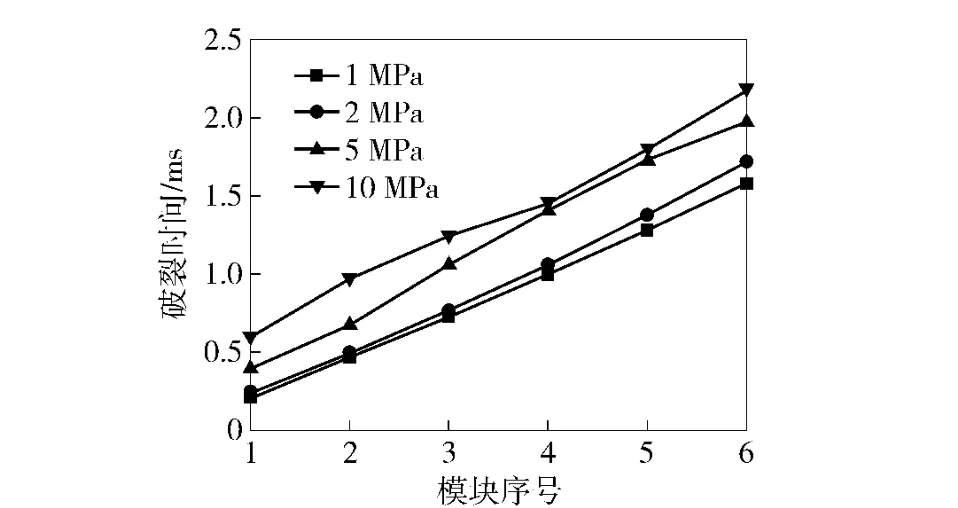
图10 不同模块强度时的模块盒破裂时间对比Fig.10 The rupture time of the modular charge cases with differen case strength

由表2 可见，随着端盖强度的增加，主装药全面点火的时间变长。端盖强度小，模块间传火顺畅，火焰能够迅速传播并对主装药点火。传火管端盖影响了火焰传播速度的同时也影响了内弹道性能。由图10 和图11 可得出，模块按序破裂，且端盖强度增加，传火通道不畅，模块破裂时间变长。

从上述结果可得到，火焰在模块间的传播受到传火管端盖的阻隔，点火波阵面不能迅速由膛底传播到弹底，难以达到主装药床同时点火。

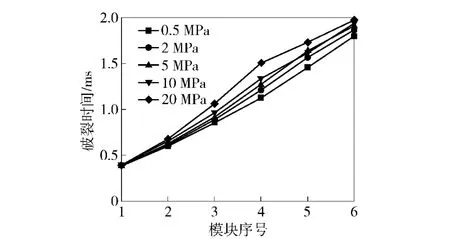
图11 不同传火管端盖强度时的模块盒破裂时间对比Fig.11 The rupture time of the modular charge cases with different tube cap strength

3 结论

本文根据模块装药结构特点，结合两相流理论，建立了改进的数学模型并求解。改进模型考虑了模块装药的点火不连续、装药不连续、模块破裂前保持密闭和模块分时破裂等特点。验证说明了所建立的模型及边界处理方法是可取的，求解的膛内压力和空隙率变化规律符合模块装药内弹道特点，可用来分析和优化模块装药内弹道性能。根据模拟结果可得出如下结论:

1)由于模块的阻隔，模块装药的火焰传播要慢于整装式装药，且随着阻隔组件强度的增加，传火性能变差。

2)各模块不是同时破裂的，破裂时间受到盒体强度和传火性能等多重影响。模块强度越强则破裂时机越晚，且从击发到全部破裂的时间越长，传火管端盖强度增加也会引起盒体的破裂时机变晚和破裂过程变长。

References)

[1]梁世超，徐文娟.模块装药的内弹道分析[J].弹道学报，2000，12(4):35 －40.LIANG Shi－chao，XU Wen－juan.The analysis on interior ballistic of modular charges[J].Journal of Ballistics，2000，12(4):35 －40.(in Chinese)

[2]余斌.刚性组合装药可燃传火管性能试验研究[J].火炸药学报，2002，25(4):69 －70.YU Bin.Experimental study on ignition and flame spreading of modular charge[J].Chinese Journal of Explosives ＆ Propellants，2002，25(4):69 －70.(in Chinese)

[3]赵毅.模块装药点传火过程的数值模拟[J].火炸药学报，2003，26(2):32 －35.ZHAO Yi.Numerical simulation for ignition and flame－spreading of modular charge [J].Chinese Journal of Explosives ＆Propellants，2003，26(2):32 －35.(in Chinese)

[4]王育维，魏建国，郭映华，等.模块装药压力波数值模拟[J].火炮发射与控制学报，2000，(4):1 －5.WANG Yu－wei，WEI Jian－guo，GUO Ying－hua，et al.Simulation of pressure wave in modular charge system[J].Journal of Gun Launch ＆ Control，2000，(4):1 －5.(in Chinese)

[5]Briand R，Tisser P Y，Reynaud C，et al.Theoretical modeling of ballistics processes of modular charge for large caliber guns[C]∥Proceedings of the 13th International Symposium on Ballistics.Stockholm:National Defense Industrial Association，1992:381 －390.

[6]Légeret G，Taïana E，Boisson D.Study of the ignition of a large caliber modular charge，computation and validation[C]∥Proceedings of the 17th International Symposium of Ballistics.Midrand:The South Africa Ballistics Organization，1998:440 －447.

[7]陆中兵，周彦煌.模块装药火炮内弹道二维两相流数值预测[J].兵工学报，2001，22(3):298 －301.LU Zhong－bing，ZHOU Yan－huang.Two－dimensional two－phase flow numerical simulation of interior ballistic processes in a gun with modular charges[J].Acta Armamentarii，2001，22(3):298 －301.(in Chinese)

[8]袁亚雄，张小兵.高温高压多相流体动力学基础[M].哈尔滨:哈尔滨工业大学出版社，2005.YUAN Ya－xiong，ZHANG Xiao－bing.Multiphase hydrokinetic foundation of high temperature and high pressure[M].Harbin:Harbin Institute of Technology Press，2005.(in Chinese)

[9]高敏，史先扬，王泽山.155 mm 火炮全等式模块装药的可行性讨论[J].弹道学报，2003，15(3):14 －18.GAO Min，SHI Xian－yang，WANG Ze－shan.The feasibility study on uni－modular charges in the modular propelling charge system[J].Journal of Ballistics，2003，15(3):14 －18.(in Chinese)