磁刺激穴位复杂脑功能网络构建与分析*

尹 宁 徐桂芝 周 茜

(河北工业大学，电磁场与电器可靠性省部共建重点实验室，天津 300130)

(2012年12月13日收到;2013年1月26日收到修改稿)

1 引言

自然界有时并非如牛顿所说的喜欢简单化，相反，现实世界中的多数系统都是由内部高度非线性相互作用的动力学系统构成的，具有复杂的相互关系和作用机理.复杂网络模型对实际系统进行了合理的抽象与简化，用节点来表示动力学子系统，用边来表示子系统之间的相互作用，这种近似虽然忽略了子系统自身内部的一些细节，但却能够反映出子系统之间的许多重要关系[1].复杂网络模型可以用来描述人类社会关系、物种捕食关系、计算机网络联接、网络病毒传播、灾害蔓延、温度变化、虚拟社区、交通系统、蛋白质相互作用等[2-8].复杂网络的研究已经引起了统计物理学、计算科学、生态学、生命科学、社会学、经济学等各个领域的极大研究兴趣，其定性和定量研究成为当今科学的一大主题.大脑是包含许多不同功能区域的复杂动力学系统，大脑功能的执行离不开脑区之间的相互作用和协调.因此，在动力学和复杂网络理论基础之上，研究跟大脑活动相关的复杂脑网络是极为必要的.

目前，复杂脑网络可分为反应神经单元解剖性连接的大脑结构网络、描述大脑统计性连接关系的大脑功能网络以及体现大脑信息流向的大脑因效网络.大脑功能网络主要反映空间上分离的不同神经元、神经元集群或脑区在时间上的相关性以及功能活动的统计依赖关系，是描述大脑动态活动交互整合的有效手段之一.大脑功能网络的研究与功能磁共振成像、脑电图和脑磁图等成像技术密不可分，涉及心理学、认知神经科学、病理学等诸多领域.Friston[9]于1994年最早开展了基于功能磁共振成像的脑功能网络研究，并给出了功能连接的定义.Stam等[10]基于脑磁图研究了阿尔茨海默病患者的大脑功能网络，结果发现患者脑功能网络的平均最短路径长度比正常人显著增加，“小世界”属性有所退化.与功能核磁共振成像和脑磁图相比，脑电图虽然空间分辨率较低且网络节点较少，但因其具有时间分辨率高、实验成本低、易于操作等优点[11]而被广泛采用.Smit等[12]利用脑电图发现脑功能网络具有小世界拓扑结构.Li等[13]研究发现在完成注意任务时，脑功能网络的聚类系数会高于睁眼无任务状态.Micheloyannis等[14]基于脑电图构建了精神分裂症患者的脑功能网络，发现其在静息状态和工作记忆任务下的局部聚类系数与正常人相比都有所下降.Fang等[15]利用脑电图数据建立了酒精成瘾症患者的脑功能网络，发现其复杂网络特征指数与正常人有明显不同，患者的信息熵明显小于正常人.

穴位刺激可以等效为大脑神经系统的一种外部刺激，对研究大脑复杂动力学系统的调控机理有重要意义，众多学者开展了针刺穴位对大脑功能区域的影响以及相关脑功能网络的研究[16,17]，从而深入分析针灸的作用机理.Li和Luo等[18,19]基于脑电图构建了针刺脑功能网络，研究发现针刺足三里具有提高脑部区域间信息交流的效果，对脑疾病可能会产生有益的影响.与针刺相比，磁刺激技术因具有无痛、无创、操作简便等优点，正在作为一种新型的穴位刺激方式应用于临床研究中，在人体神经功能调控、疾病治疗与康复理疗等方面具有很好应用前景.现有的磁刺激穴位研究[20]主要侧重单通道脑电信号的特性分析，不能深刻揭示磁刺激穴位过程中大脑各个脑区之间的相互联系.本文采用非线性复杂网络理论分析方法，首次基于脑电图数据构建了磁刺激穴位复杂脑功能网络，从大脑的整体性角度入手研究磁刺激穴位多通道脑电信号的关联特性和整体特征，并着重研究体表穴位磁刺激对大脑功能网络拓扑结构及特征参数的影响，为更深入的研究体表穴位磁刺激对大脑活动及神经功能调控的影响开辟新的途径.

2 基于脑电数据的复杂脑功能网络的构建

2.1 脑电数据采集与预处理

7名健康在校学生作为被试自愿参加了穴位磁刺激实验，其中4名男生，3名女生，年龄集中在23—25岁之间，皆为右利手，无任何精神病史.实验前告知各被试在整个实验过程中保持安静闭眼并且清醒的状态.

选取右侧内关穴作为刺激目标，该穴位与大脑神经调节有密切关联.磁刺激实验采用英国Magstim公司的Rapid2重复脉冲磁刺激仪.刺激线圈为8字形线圈，刺激强度为1.76 T，刺激频率为1 Hz和3 Hz，刺激时间各120 s，刺激模式为重复刺激模式，各参数选择均满足安全性要求.实验过程中保持环境安静，室温约为22°C，尽可能避免被试和环境受干扰.利用美国NeuroScan脑电记录分析系统同步采集了刺激前、1 Hz刺激、1 Hz刺激后、3 Hz刺激、3 Hz刺激后5种状态下的64导头皮脑电信号，采样频率为1000 Hz.将磁刺激实验过程中采集的脑电信号剔除明显漂移的数据、去除眼电伪迹并进行0.5—40 Hz的带通滤波等预处理.分别截取每个被试刺激前、1 Hz刺激、1 Hz刺激后、3 Hz刺激、3 Hz刺激后几个阶段各50 s的脑电数据，进行下一步复杂脑功能网络的构建与分析.

2.2 脑电信号关联特性分析

互信息作为一种双通道信号非线性分析方法，广泛应用于脑电分析处理领域，可以用来衡量任意两两电极测量通道间脑电信号的相互关联关系.任意双通道脑电信号可分别用离散随机变量X和Y表示，它们之间的互信息可以表示为

其中，H(X)，H(Y)分别表示随机变量X和Y的信息熵，H(XY)表示X和Y之间的联合熵.

熵的概念最早起源于物理学，用于度量一个热力学系统的无序程度.Shannon[21]借鉴了热力学的概念将熵引入到信息论，把排除了冗余后的平均信息量称为信息熵，解决了对信息的量化度量问题.任意双通道脑电信号X和Y的信息熵可以分别表示为

其中，pxi和pyj分别为随机变量X和Y的概率密度函数.以离散随机变量X为例，用直方图法对其概率密度函数pxi进行估计，即将X分为b个区域，统计X落在各个区域的概率.

X和Y之间的联合熵可以表示为

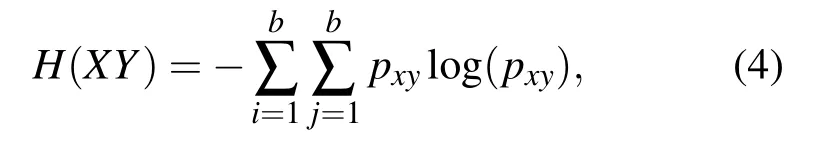
其中，pxy为随机变量X和Y的联合概率密度函数.

通过上述方法可以分别计算每个通道脑电信号的信息熵以及任意两个通道脑电信号之间的联合信息熵，从而可以得到各通道脑电信号间的互信息矩阵.为统一度量标准，将所得的互信息进行了归一化.归一化互信息的大小反映了通道间信号关联程度的高低，越接近1，表示信号间的关联程度越高，反之表示关联程度越低.

2.3 复杂脑功能网络构建

复杂脑功能网络的构建关键有三步：一是如何定义网络节点，二是如何选取阈值，三是如何定义网络连接边.

1)节点选取 将每个电极通道所测量的大脑区域作为要构建的复杂脑功能网络的节点，通道脑电信号间的归一化互信息矩阵作为节点关联关系矩阵.

2)阈值选取 在得到完整的节点关联关系矩阵后，需要确定一个合适的阈值来构建二值矩阵.本文在阈值的选取时主要遵循以下原则：避免全连接、保证连接稀疏性且孤立点尽量少.当节点间的关系强度大于阈值时，二值矩阵相应位置的元素取值为1，反之为0.

3)边的连接 当二值矩阵元素为1时，在所对应节点之间建立一个连接边，反之则不建立连接边.从而可以构建出刺激前、1 Hz刺激、1 Hz刺激后、3 Hz刺激、3 Hz刺激后几种状态下的复杂脑功能网络.

3 基于复杂网络理论的脑网络分析方法

3.1 复杂脑网络的特征参数

采用平均度、平均聚类系数、平均路径长度、全局效率等复杂网络测度方法对所建立的大脑功能网络进行评价.通过对比研究刺激前、刺激中和刺激后的脑功能网络拓扑结构的异同，尝试探索大脑在外界电磁刺激下的功能拓扑动态变化过程和功能活动机理.

1)平均度 度是复杂网络节点的属性中最简单但也是最重要的性质.一个节点的度定义为与它相连的节点的数目.从直观上看，一个节点的度越大，意味着该节点重要性越强[22].网络的平均度可以通过下式计算：

其中，N表示网络中的节点个数，Di表示网络中第i个节点的度.

2)平均聚类系数 聚类系数是衡量网络内部聚集程度的重要参数.复杂脑功能网络的聚类系数反映了大脑皮层的功能性分化机理，即局部脑功能区域内的神经元之间连接紧密程度[22].节点i的聚类系数可以表示为

其中，Ei表示与节点i相连的ki个节点之间实际存在的边数，Mi表示与节点i相连的ki个节点之间最多可能存在的边数.对网络中所有节点的聚类系数取平均值可以得到整个网络的平均聚类系数，即

3)平均路径长度 平均路径长度指网络中任意两个节点间最短距离的平均值，是研究复杂特性的关键参数[22].不考虑节点到其自身的距离对平均路径长度的影响，脑功能网络中任意节点间的平均路径长度可由公式表示为

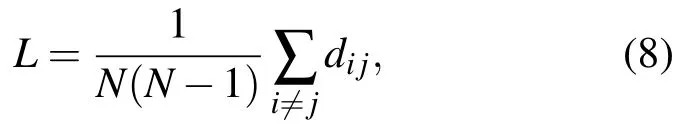
其中，N表示网络中节点的个数，dij表示连接两个节点i和 j的最短路径上边的个数，也称为两个节点之间的距离.

4)全局效率 全局效率是衡量网络中信息传递快慢的一个综合指标[23]，它可以用来评价脑电信息是如何在复杂脑功能网络中快速传递的，具体可以表示为

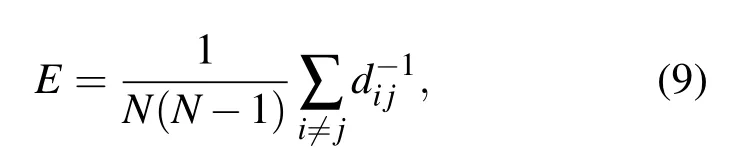
其中，N表示网络中节点的个数，dij表示连接两个节点i和 j的最短路径.

从定义上来看，平均路径长度和全局效率都是衡量信息在脑功能网络中的传递快慢的指标，主要用来刻画大脑在特定状态下能量及物质消耗的是否“经济”.若脑功能网络的平均路径长度较短，即说明其全局效率较高，信息在该网络中传递速度也较快.

3.2 复杂脑网络的“小世界”属性

由于大脑的复杂性，规则网络和随机网络并不能很好地反映出脑网络的特性.小世界网络是介于规则网络和随机网络之间的一种网络模型，具有较短的平均路径和较高的聚类系数.小世界网络概念的提出，为量化研究复杂脑网络的性质和脑功能性疾病提供了新手段.Watts和Strogatz建议将随机网络作为基准来量化网络的“小世界”属性[24].

如果所研究的网络相对于相同规模(具有相同节点数和网络平均度)的随机网络而言具有较大的聚类系数和近似的最短路径长度，即满足

则证明该网络属于“小世界”网络范畴.其中，Creal和Lreal分别代表所构建的真实网络的平均聚类系数和平均路径长度，Crand和Lrand分别代表随机网络的平均聚类系数和平均路径长度.

两个度量指标可以统一成一个“小世界”属性综合指标σ=γ/λ.当σ＞1时，网络具有“小世界”属性，且σ越大说明该网络的“小世界”属性越强[25,26].

4 结果与分析

4.1 复杂脑功能网络构建结果

阈值T的选取对大脑功能网络的构建有重要的影响，探讨复杂脑网络特征随阈值的变化情况是非常必要的，作为基准态的刺激前状态下的脑功能网络特征参数随阈值的变化曲线如图1所示.

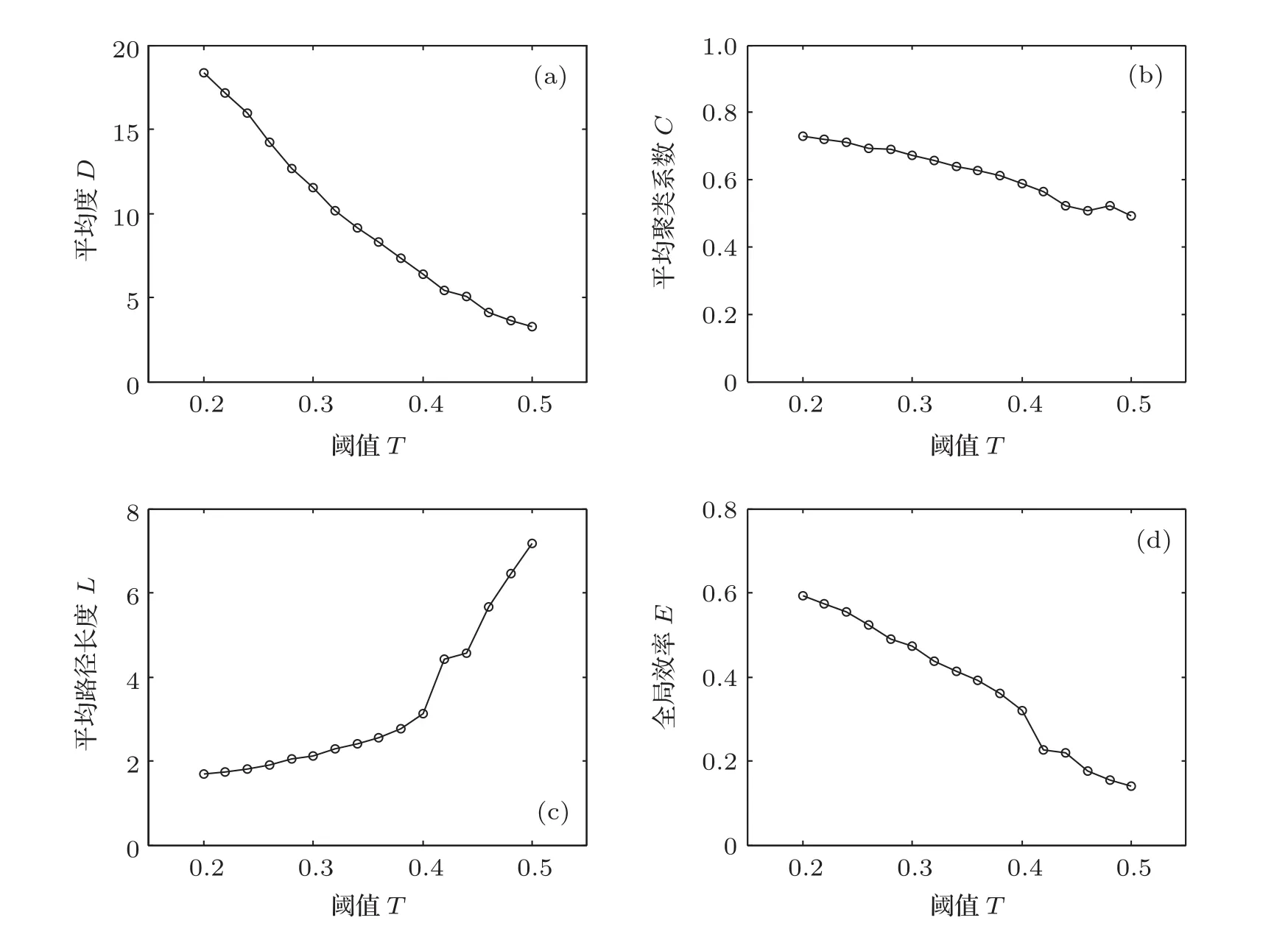
图1 脑功能网络特征参数随阈值的变化曲线 (a)平均度;(b)平均聚类系数;(c)平均路径长度;(d)全局效率

由于当阈值T＜0.2时，磁刺激穴位各个状态下的脑功能网络近似为全连接状态且特征参数基本趋于一致，不具有比较意义;而当阈值T＞0.5时，大脑功能网络的孤立点大量增加，也失去了相应的研究意义.因此，图中给出了从阈值T=0.2逐步递增到T=0.5过程中的特征参数变化结果.从图中可以看出，脑功能网络的平均度D、平均聚类系数C、全局效率E均随着阈值T的逐步增大而减小，而平均路径长度L随阈值T的逐步增大而增大.

考虑到阈值对脑功能网络特征参数的重要影响，本文在阈值选取过程中主要兼顾考虑了以下因素：尽可能保证脑功能网络连接的稀疏性，尽量减少孤立点个数.以被试2为例，其刺激前、1 Hz刺激、3 Hz刺激三个状态下的脑功能网络如图2所示，其中阈值T=0.4.从图中可以看出，1 Hz刺激和3 Hz刺激与刺激前状态相比，大脑功能网络的功能连接数有所增加，且3 Hz刺激时变化更为显著.该阈值的选取保留了几种状态的差异性，同时脑功能网络的连接较为稀疏且孤立点很少，满足阈值选取要求.

4.2 磁刺激穴位对复杂脑网络特征参数的影响

按照上述阈值选取原则，分别构建了所有被试在磁刺激穴位不同状态下的脑功能网络.从直观上观察，被试在磁刺激穴位过程中大脑的功能网络的连接数量发生了不同程度的变化.为了更加深入且定量的研究磁刺激对大脑功能网络产生的影响，分别针对不同状态脑功能网络的平均度D、平均聚类系数C、平均路径长度L和全局效率E四个参数进行了对比分析，结果如图3所示.从图中可以看出，1 Hz刺激与刺激前状态相比，大部分被试脑功能网络的平均度D、平均聚类系数C和全局效率E有所升高，平均路径长度L有所降低.3 Hz刺激与刺激前和1 Hz刺激状态相比，所有被试脑功能网络的平均度、平均聚类系数和全局效率均呈现增长趋势，平均路径长度减小，且经过配对样本t检验，结果有显著性差异(p＜0.05).

复杂脑功能网络几个特征参数并不是孤立存在的，它们之间存在着内在的联系.平均聚类系数和平均路径长度随平均度的变化曲线如图4所示.从图中可以看出，平均聚类系数随着平均度的增加呈现明显的上升趋势，而平均路径长度则随着平均度的增加而递减，说明更高的边密度导致更多的节点聚集到了一起，从而使节点间的距离缩短.

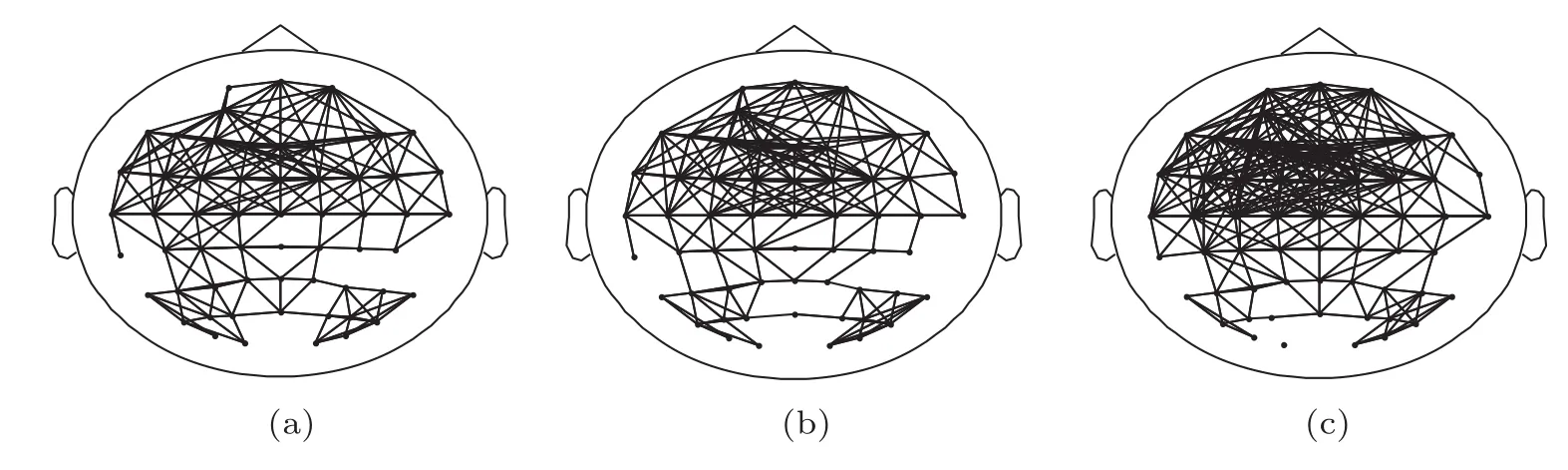
图2 大脑功能网络图 (a)刺激前;(b)1 Hz刺激;(c)3 Hz刺激

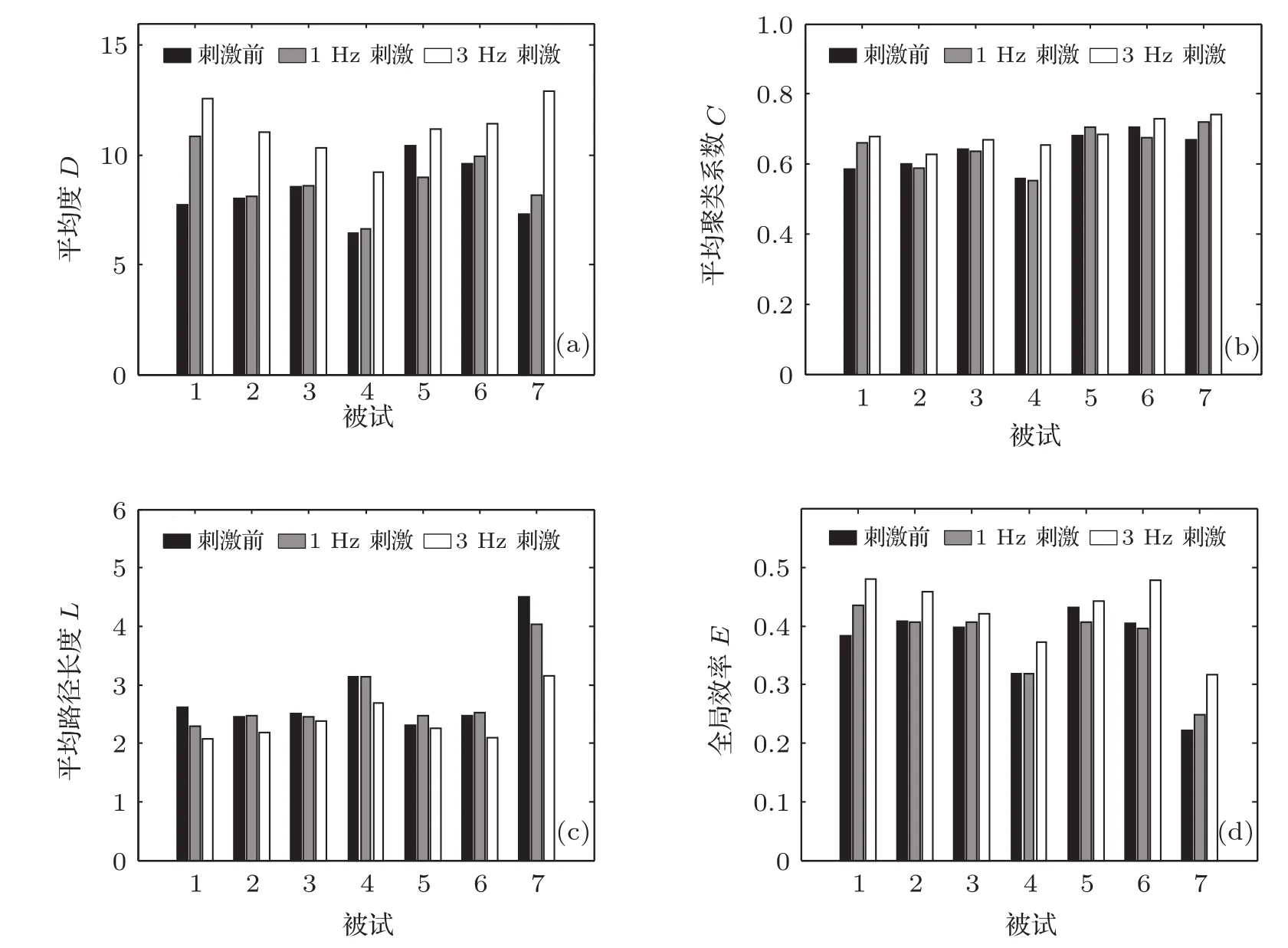
图3 不同磁刺激状态下大脑功能网络特征参数对比图 (a)平均度;(b)平均聚类系数;(c)平均路径长度;(d)全局效率

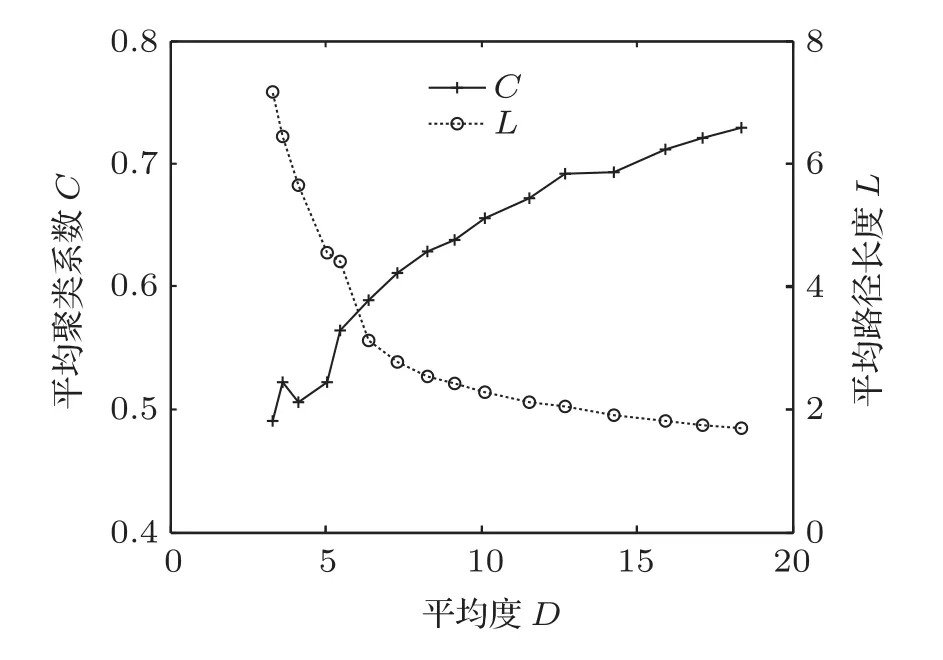
图4 平均聚类系数和平均路径长度随平均度的变化曲线

结合几个特征参数之间的内在联系，以及复杂脑功能网络的聚类性和结构化分析结果表明，适当频率的内关穴位磁刺激会使复杂脑功能网络节点间的连接数增加，网络的平均度随之增加;相邻节点之间的联系变得更加紧密，即平均聚类系数增加;节点之间的距离随之缩短，于是网络的平均路径长度减小而全局效率提高.这一系列变化的结果使得复杂脑功能网络区域间的内部连通性变强，对信息交流效果产生一定的改善作用.

4.3 磁刺激穴位复杂脑网络的小世界属性

所构建的脑功能网络与具有相同规模(相同节点和平均度)的随机网络的拓扑结构对比结果如图5所示.从图中可以直观看出二者在网络连接结构上具有明显的差异性.

图6给出了磁刺激为3 Hz时大脑功能网络的特征参数与相应具有相同规模随机网络的比较结果.其中，C3和L3分别代表了3 Hz刺激脑功能网络的平均聚类系数及平均路径长度.从结果可以看出，3 Hz刺激时的脑功能网络的平均聚类系数远远大于相应的随机网络，而平均路径长度与随机网络较为接近.

所有被试不同状态下的复杂脑功能网络“小世界”属性综合参数σ如表1所示.由结果可以看出，所有被试脑功能网络的综合参数σ均大于1，可以说明所构建的磁刺激穴位大脑功能网络均具有“小世界”属性，即在保证有较短的平均路径的同时又具有较高的聚类系数.从结果还可以发现，3 Hz刺激时的综合参数σ均高于刺激前和1 Hz刺激时的σ，表明3 Hz穴位磁刺激时复杂脑功能网络的“小世界”属性有所增强，使得网络中的信息传递更加高效.

图5 脑功能网络与相同规模随机网络的结构对比 (a)脑功能网络;(b)随机网络

图6 大脑功能网络与相同规模随机网络特征参数对比 (a)平均聚类系数;(b)平均路径长度

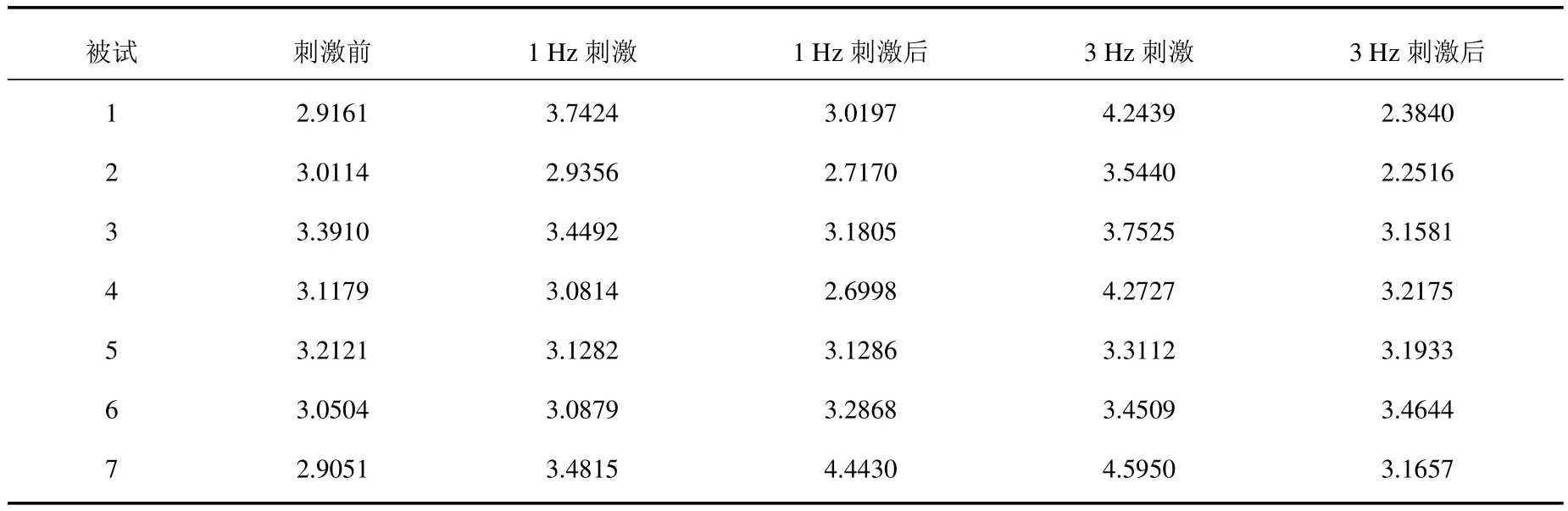
表1 不同状态下的脑功能网络“小世界”属性综合参数σ

5 结论

本文基于非线性和复杂网络分析方法，从整体性角度研究了磁刺激内关穴对大脑功能连接产生的影响.利用互信息方法对多通道脑电信号进行了非线性时域关联特性分析，并在此基础上构建了磁刺激穴位不同状态下的大脑功能网络.利用复杂网络测度方法对静息态以及不同刺激态下的大脑功能网络结构分布、特征参数、小世界属性进行了深入研究与分析，探索了体表穴位磁刺激时大脑功能网络拓扑结构的动态变化.结果发现，3 Hz磁刺激与刺激前相比，复杂脑功能网络的平均度、平均聚类系数和全局效率均有显著升高，平均路径长度显著降低.同时，3 Hz刺激时脑功能网络的“小世界”属性也有所增强，信息在大脑区域间的传递更加高效.

本文首次开展了体表穴位磁刺激复杂脑功能网络的分析和研究，将各个脑区作为整体来探索磁刺激穴位对大脑产生的影响，为磁刺激穴位的研究开拓了新思路和新方法.研究结果表明，适当频率的内关穴位磁刺激使得复杂脑功能网络的节点连接有所增加，相邻节点之间的联系更加紧密，节点之间的距离缩短，网络区域间的连通性增强，信息交流效果有所改善，对一些大脑功能性疾病可能会产生有益的影响.磁刺激穴位复杂脑功能网络研究为脑功能性疾病的康复理疗提供了新的思路，值得继续开展大量实验和理论研究进行深入探讨.

[1]Zhang F F，Zheng Z G 2012 J.ShanghaiUniv.Sci.Tech.34 138(in Chinese)[张方风，郑志刚2012上海理工大学学报34 138]

[2]Kaiser-Bunbury C N，Muff S，Memmott J，Mller C B，Ca flisch A 2010 Ecol.Lett.13 442

[3]Ouyang M，FeiQ，Yu M H 2008 Acta Phys.Sin.57 6763(in Chinese)[欧阳敏，费奇，余明晖2008物理学报57 6763]

[4]Zhou L，Gong Z Q，ZhiR，Feng G L 2008 Acta Phys.Sin.57 7380(in Chinese)[周磊，龚志强，支蓉，封国林2008物理学报57 7380]

[5]Zhang L，Liu Y 2008 Acta Phys.Sin.57 5419(in Chinese)[张立，刘云2008物理学报57 5419]

[6]Zheng X，Chen J P，ShaoJ L，Bie L D 2012 Acta Phys.Sin.61 190510(in Chinese)[郑啸，陈建平，邵佳丽，别立东2012物理学报 61 190510]

[7]Liu H K，Zhou T 2007 Acta Phys.Sin.56 106(in Chinese)[刘宏鲲，周涛2007物理学报56 106]

[8]ColomboE，Alcalay M，PelicciP G 2011 Oncogene 30 2595

[9]Friston K J 1994 Hum.Brain Mapp.2 56

[10]Stam C J，de Haan W，Daffertshofer A，Jones B F，Manshanden I，van Cappellen van Walsum A M，Montez T，Verbunt J P A，de Munck J C，van Dijk B W，Berendse H W，Scheltens P 2009 Brain 132 213

[11]LiL，Jin Z L，LiB 2011 Acta Phys.Sin.60 048703(in Chinese)[李凌，金贞兰，李斌2011物理学报60 048703]

[12]Smit D J A，Stam C J，Posthuma D，Boomsma D I，de Geus E J C 2008 Hum.Brain Mapp.29 1368

[13]LiL，Jin Z L，LiB 2011 Chin.Phys.B 20 038701

[14]Micheloyannis S，Pachou E，Stam C J，Breakspear M，Bitsios P，Vourkas M，ErimakiS，Zervakis M 2006 Schizophr.Res.87 60

[15]Fang X L，Jiang Z L 2007 Acta Phys.Sin.56 7330(in Chinese)[方小玲，姜宗来2007物理学报56 7330]

[16]Bian R J，Wang J，Han C X，Deng B，WeiX L，Che Y Q 2011 Acta Phys.Sin.60 118701(in Chinese)[边洪瑞，王江，韩春晓，邓斌，魏熙乐，车艳秋2011物理学报60 118701]

[17]Han C X，Wang J，Che Y Q，Deng B，GuoYi，GuoY M，Liu Y Y 2010 Acta Phys.Sin.59 5881(in Chinese)[韩春晓，王江，车艳秋，邓斌，郭义，郭永明，刘阳阳2010物理学报59 5881]

[18]LiN，Wang J，Deng B，WeiX L，Che Y Q，Jia C H，GuoY，Wang C 2011 Acup.Res.36 278(in Chinese)[李诺，王江，邓斌，魏熙乐，车艳秋，贾晨辉，郭义，王超2011针刺研究36 278]

[19]LuoX L，Wang J，Han C X，Deng B，WeiX L，Bian H R 2012 Chin.Phys.B 21 028701

[20]Xu G Z，Zhang X，Yang Q X，Yang S，Yan W L 2010 Trans.Chin.Electrotech.Soc.25 34(in Chinese)[徐桂芝，张秀，杨庆新，杨硕，颜威利2010电工技术学报25 34]

[21]Shannon C E 1949 BellSyst.Tech.J.28 656

[22]Albert R，BarabasiA L 2002 Rev.Mod.Phys.74 47

[23]Latora V，MarchioriM 2001 Phys.Rev.Lett.87 198701

[24]Watts D J，Strogatz S H 1998 Nature 393 440

[25]Humphries M D，Gurney K，Prescott T J 2006 Proc.R.Soc.Lond.B 273 503

[26]SuiD N，ZhaoQ B，Tang Y Y 2010 Chin.Phys.Lett.27 018702