AsCl自由基的基态及激发态的势能函数与光谱常数的研究*

朱遵略 郎建华 乔 浩

(河南师范大学物理与电子工程学院，新乡 453007)

(2012年12月19日收到;2013年2月24日收到修改稿)

1 引言

我国是白砷的最大生产国，囊括了接近全球产量的50%.砷与其化合物被运用在农药与许多种的合金中.三氯化砷是一种无机砷化合物，是含有剧毒而无色的液体.AsCl自由基是化学合成三氯化砷反应的中间体具有独特的光谱性质，因此对砷及其化合物的研究有着现实的意义.1967年，Basco等[1]用等温闪光光分解AsCl3分子，在245nm附近观测到一组violet-degraded键的吸收光谱，他们认为是AsCl自由基的吸收光谱.得到的光谱常数ωe和ωeχe分别是443 cm-1和2 cm-1.Kruse等[2]于1984年用放电流动系统在近红外光谱范围观测到AsCl和AsBr的b0+→X10+，X21键的化学发光，通过分析光谱得到AsCl的光谱常数分别是：

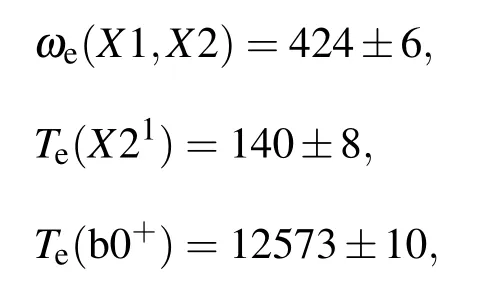
2006年David等[3]用密度泛函理论和大范围内的从头算方法得到一系列的AsCl自由基的光谱常数Re和ωe.关于AsCl自由基的其他光谱常数及激发态的势能函数、光谱常数未见报道.为了更全面的了解AsCl自由基的性质，用于进一步的动力学计算，需要更高精度的理论计算.

本文首先推导了AsCl自由基的基态及激发态合理的离解极限，然后利用能充分反映相关能的多组态相互作用(MRCI+Q)[4,5]方法和相关一致基aug-cc-pV5Z基组[6,7]系统地对AsCl自由基的基态和多个低电子激发态的势能曲线进行了计算.最后，通过求解双原子分子核运动的径向Schrdinger方程，得到了AsCl自由基的分子常数.

2 理论方法与计算

2.1 AsCl自由基的离解极限

根据原子分子反应静力学中的分离原子法[8]由广义Wigner-Witmer规则确定可能的电子状态.As和Cl原子的基电子结构分别为4Su和2Pu，属于SU(n)群，AsCl属于C∞v群.当基态As(4Su)与Cl(2Pu)原子对称性降低生成AsCl自由基时SU(n)群的不可约表示可分解为C∞v群的不可约表示的直和，通过直积和约化可得C∞v群的不可约表示，即AsCl自由基的可能电子状态.As(4Su)和Cl(2Pu)分别分解为C∞v群的不可约表示的直和为

2.2 AsCl自由基的光谱常数

多组态相互作用方法(MRCI)是一种系统的从头计算方法，是一种可靠的势能曲线计算方法.MOLPRO使用的是Abelian点群，对于对称性是C∞v的线性分子AsCl由其子群C2v群替换.C2v共有4种类型的轨道，其对应的不可约表示为a1/b1/b2/a2.对于含有50个电子的AsCl自由基，分析其共有27个默认参与运算的分子轨道，分别是14个A1，6个B1，6个B2和1个A2轨道.其中8个属于开壳层轨道(4A1，2B1，2B2)，分别对应于As原子的4s4p和Cl原子的3s3p轨道.

在计算过程中我们发现，对于3Σ-，1Δ，1Σ+态计算只采用这27个分子轨道(14A1，6B1，6B2，1A2)时所得的势能曲线出现跳变.为了得到光滑的势能曲线，我们将更多的轨道放入活化空间.对于3Σ-态，我们将2个额外的A1轨道放入活化空间;对于1Δ，1Σ+态参与计算的分子轨道是 15A1，6B1，6B2，1A2，此时所得势能曲线是光滑的.

本文对As和Cl原子都使用了相关一致基aug-cc-pV5Z，即对As原子由原始高斯基组(26s，17p，13d，3f，2g，1h)，并增加了扩散函数 (1s，1p，1d，1f，1g，1h).Cl原子是 (20s，12p，4d，3f，2g，1h)，扩散函数是 (1s，1p，1d，1f，1g，1h).该基组是 Dunning[6,7]提出的含有扩散函数的5z相关一致基，能很好的描述原子间距离较大时的相互作用情况.本文采用单点扫描计算获得势能曲线，在0.12—0.615 nm范围内进行，原子间距离的变化步长为0.005 nm，共扫描了100个势能点.全部计算是在MOLPRO2008.1程序包[9]中完成的.为了得到准确的光谱数据，我们在整个计算范围内考虑了相对论效应对光谱常数计算的影响和Davidson修正[10]空间大小的不一致性，结果所得势能曲线光滑且完全收敛.

3 结果与讨论

3.1 光谱常数

AsCl自由基的各个电子态的平衡位置大致相同，因此每条势能曲线的计算范围是0.12—0.615 nm，扫描步长为0.005 nm，共计算了100个点.扫描得到的势能曲线如图1所示.表1列出了AsCl自由基的基态及激发态的光谱常数.为便于比较，表1列入了实验值[1,2].

1984年，Kruse等[2]用放电流动系统在近红外光谱范围观测到AsCl自由基的光谱常数ωe(X1，X2)为424±6 cm-1和ωe(b0+)=443±8 cm-1.发现其基态数据与Basco等[1]的实验数据ωe=443 cm-1相差很大，而与ωe(b0+)=443±8 cm-1相一致，于是他们指出Basco等[1]的实验数据为b0+态而不是基态.结合理论计算[3]及本文的计算可以肯定Basco等[1]的实验数据为1Σ+态.2006年David等[3]用密度泛函理论和从头算方法得到一系列的AsCl自由基的光谱常数Re和ωe.最后发现在QCISD/6-311++G(3df，3pd)理论水平下得到的ωe和实验值[2]相符合，其偏离实验数据为2.24 cm-1(0.5283%)，但是，这些计算是基于单参考组态方法而且用的基组较小对相关能的计算和激发态的描述精度不高.对于3Σ-和1Σ+态本文得到的ωe值偏差分别为1.319 cm-1(0.311%)和0.34 cm-1(0.0767%)显然优于文献[3]的理论计算，说明本文所采用的计算方法是可靠的，计算得到的光谱常数可作为进一步实验测量和理论计算的参考.

图1 AsCl自由基基态和低激发态的势能曲线计算水平MRCI+Q/aug-cc-pV5Z

表1 AsCl自由基基态和低激发态的光谱常数及与实验结果和其它理论结果的比较

3.2 振动能级及惯性转动常数和离心畸变常数

虽然没能找到AsCl自由基的振动能级、转动惯量、离心畸变常数的理论及实验值，无法与本文所计算的结果进行比较.但是表1中的计算结果与实验值较为相符.因此.表2和表3中的计算数据是可靠的.

表2 MRCI/aug-cc-pV5Z理论水平下AsCl自由基基态(3Σ-)及激发态(1Δ)的振动能级、转动惯量和离心畸变常数

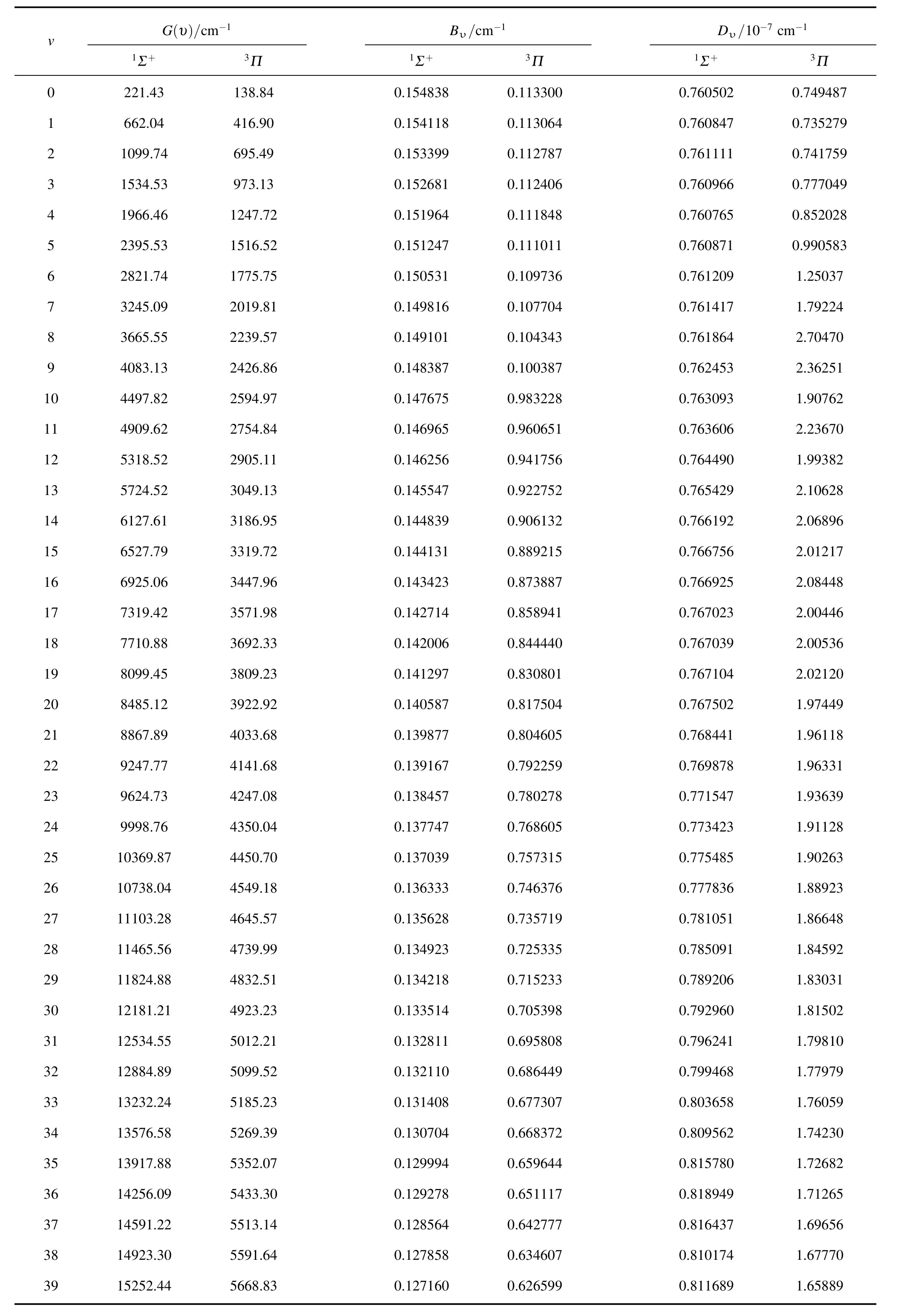
表3 MRCI/aug-cc-pV5Z理论水平下AsCl自由基态1Σ+和3Π态的振动能级、转动惯量和离心畸变常数

4 结论

本文对AsCl自由基的基态(3Σ-)和3个电子激发态 (1Δ，1Σ+，3Π)运用含 Davidson修正的多参考组态相互作用(MRCI+Q)方法和扩散基组augcc-pV5Z进行了单点能扫描计算，根据原子分子反应静力学推导确立了各条曲线对应的电子态及离解极限.最后通过求解径向Schrdinger方程，找到了J=0时AsCl自由基的基态及激发态的部分40个振动态，并得到了每一振动态的振动能级、离心畸变常数、转动惯量等分子常数.所得数据为以后AsCl自由基实验和理论上的研究提供可靠的理论依据.

[1]BascoN，Yee K K 1967 J.Chem.Commun.1255

[2]Kruse H，Winter R，Fink E H，Wildt J，ZabelF 1984 Chem.Phys.Lett.111 100

[3]David R Urban，Jennifer Wilcox 2006 J.Phys.Chem.110 5847

[4]Werner H J，Knowles P J 1988 J.Chem.Phys.89 5803

[5]Knowles P J，Werner H J 1988 Chem.Phys.Lett.145 514

[6]Woon D E，Dunning T H 1993 J.Chem.Phys.98 1358

[7]Dunning T H，Jr 1989 J.Chem.Phys.90 1007

[8]Zhu Z H 2007 Atomic and Molecular Reaction Statics(Beijing：Science Press)(in Chinese)[朱正和2007原子分子反应静力学(北京：科学出版社)第39页]

[9]Werner H J，Knowles P J，Lindh R，Manby F R，Schtz M，CelaniP，Korona T，Mitrushenkov A，Rauhut G，Adler T B，Amos R D，Bernhardsson A，Berning A，Cooper D L，Deegan M J O，Dobbyn A J，Eckert F，GollE，HampelC，Hetzer G.，Hrenar T，Knizia G.，KpplC，Liu Y，Lloyd A W，Mata R A，May A J，McNicholas S J，Me yer W，Mura M E，Nicklass A，PalmieriP，P flger K，Pitzer R，Reiher M，Schumann U，StollH，Stone A J，TarroniR，Thorsteinsson T，Wang M，Wolf A 2008 A Package of ab InitioPrograms

[10]Langhoff S R，Davidson E R 1974 Int.J.Quantum Chem.861

[11]Krogh J W，Lindh R，Malmqvist P A，Roos B O，Veryazov V，Widmark P O 2009 User ManualMolcas Version 7.4(Lund：Lund University)