原子激发态在高频强激光作用下的光电离研究*

田原野 郭福明 曾思良 杨玉军

1)(吉林大学原子与分子物理研究所，长春 130012)

2)(北京应用物理与计算数学研究所，计算物理重点实验室，北京 100088)

3)(北京应用物理与计算数学研究所，高能量密度物性数据中心，北京 100088)

(2013年1月14日收到;2013年2月26日收到修改稿)

1 引言

随着强激光脉冲技术的发展，人们已经能够利用激光脉冲与原子分子相互作用，观察到高次谐波发射(HHG)，阈上电离(ATI)，非序列双电子电离等强场物理现象[1-3].其中一个典型的非微扰物理现象就是ATI.一般而言，ATI谱呈现出两个平台结构，分别对应束缚态电子的直接电离和再散射电离过程.对此，人们已经进行了广泛的研究[4-11].此外，ATI光电子能谱还可以用于探测激光脉冲的载波包络相位[12,13]，以及原子、分子的内部结构[14,15].

长期以来，高频强场与原子分子的相互作用多集中于理论研究.如，原子的动力学稳定问题：在动力学稳定区域，在高频强激光作用下，光电子谱呈现出明显的干涉相图，有复杂的峰值结构.这些结构的产生可以归结为在激光脉冲上升沿和下降沿，电离电子之间的干涉效应[16,17].随着HHG和自由电子激光技术的发展，尤其是在德国(Free-electron Laser in Hamburg)，美国 (Linac Coherent Light Source)以及日本(Spring-8 Compact SASE Source)的自由电子光源装置的服役，实验上已经可以获得亮度很高、波长很短的激光脉冲[18-23].因此从实验上利用高频强激光精细研究原子的电离过程成为可能.

本文将聚焦于高频强场与激发态原子的相互作用问题，着重考察阈值附近ATI光电子能谱和动量角度分布.系统考察ATI谱与体系初态间的关联，并研究如何对体系初态的波函数进行识别的新方案.与之前人们常采用的HHG信号对原子、分子波函数识别的方案不同.在HHG方案中，根据“三步”模型，初态电子要经历电离、在激光场中的运动，和再散射三个过程才能和谐波信号关联起来.相比之下，本文拟采用的方案更为直接，只利用直接电离信号对体系的初态进行识别.从原则上讲，信噪比更高.

若无特殊说明，本文均采用原子单位.

2 理论方法

为了描述激发态原子在强激光作用下的光电子发射谱，我们采用含时伪谱方案，在动量空间求解体系的含时薛定谔方程[24].在速度规范下和偶极近似下，原子在强激光场作用下的含时薛定谔方程为

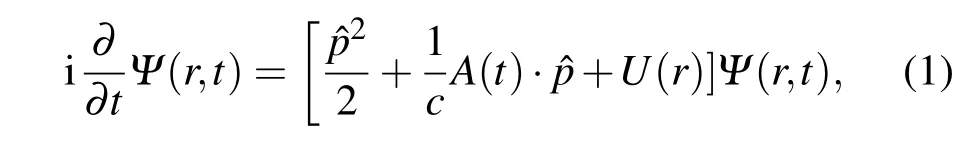
这里，c是光速，A(t)是激光场的矢势，U(r)是原子的库仑势.动量空间的波函数Φ(k,t)可以由坐标空间的波函数Ψ(r,t)做傅里叶变换得到

将方程(2)代入方程(1)，可以得到动量空间的含时薛定谔方程，该方程是一个微分积分方程

采用含时广义伪谱方案[24]，在动量空间求解(3)式，得到体系任意时刻的含时波函数.在激光脉冲结束时，将体系的波函数向无外场时体系的本征态做投影，可以得到各态的布居系数.根据散射态的定义，计算得到对应的光电子谱角分布[28].若bl(ε,t)为能量归一化的连续态布居振幅.则一重微分电离截面为

3 结果与分析

选择入射激光电场方向为z方向的线偏振激光脉冲，激光脉冲的电场矢势为

利用伪谱方案，首先计算了氢原子的各个本征态.图1给出了氢原子5s，5p，5d和5f在动量空间的波函数.在含时伪谱方案中，我们采用变步长的方法，在动量很小的区域，选择足够多的计算网格点，对于空间较大的区域，选择的计算网格点较少，同时可以保证计算的边界足够大.选择动量径向网格点数目为1000时，就可以将基态能量和精确解差值降低到10-9.进而为进一步的波函数含时演化奠定基础.

图1 动量空间氢原子激发态波函数 (a)5s;(b)5p;(c)5d;(d)5f

基于时间演化得到的含时波函数，我们计算了初态为不同激发态光电子能谱.这里选择体系的初态分别为氢原子的 1s，2s，3s，4s和 5s.为了一般起见，设入射激光的持续时间为30个光学周期，激光的频率为1个原子单位，强度为1013W/cm2.在该电场作用下，体系不同初态的ATI光电子能谱如图2(a)所示.从图中可以看出，ATI谱呈现出明显的峰值结构.随着不同初态主量子数n的增加，第一个ATI的峰值位置逐渐向高能移动.峰值位置满足公式Ek=ω-Ip-Up，这里ω是激光的频率，Ip和Up分别为体系的电离能和激光场的有质动力势.图2(b)给出了激光强度为1014W/cm2的结果.由于在两组激光强度下，激光场的有质动力势的数值很小，可以忽略不计，因此ATI光电子谱的峰值位置仅和初态的Ip相关.利用这一规律，在一定的激光强度范围内，可以对初态的主量子数进行判断.

为了研究如何对初态波函数的角量子数进行识别，我们进一步研究了不同初态的光电子谱动量角度分布.不失一般性，设入射激光的频率为1，脉冲强度为1013W/cm2，τR为5个光学周期，假设体系的初始状态分别为氢原子的5s，5p，5d和5f.在该激光场的作用下，不同初态的光电子动量角度分布如图3所示.从图中可以看出，对于不同的初态，在关注的动量范围内，主要有两个发射区域，一个是在动量为0附近，另一个是在动量为1.4附近.在这个能量范围内，都是以单光子电离过程为主.对于某一个初态，由于单光子吸收，其对应的量子数增加1.各个不同初态的差别在于角度的分布差别：随着角度量子数l的增加，角度分布中花瓣的数目相应地增加到2(l+1).该光电子动量角度分布环呈现规律的增加.

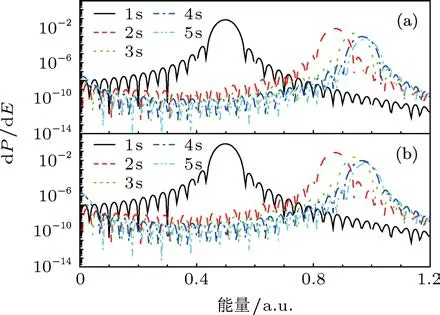
图2 入射激光为30个周期，频率为1 a.u.，强度分别为 (a)1013W/cm2;(b)1014W/cm2，原子体系初态分别为 1s，2s，3s，4s和5s的ATI谱

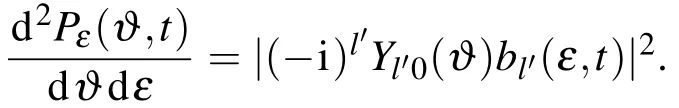
图3 入射激光为5个周期，频率为1 a.u.，强度为1013W/cm2，(a)，(b)，(c)和(d)分别对应原子体系初态为5s，5p，5d和5f的光电子动量角度分布

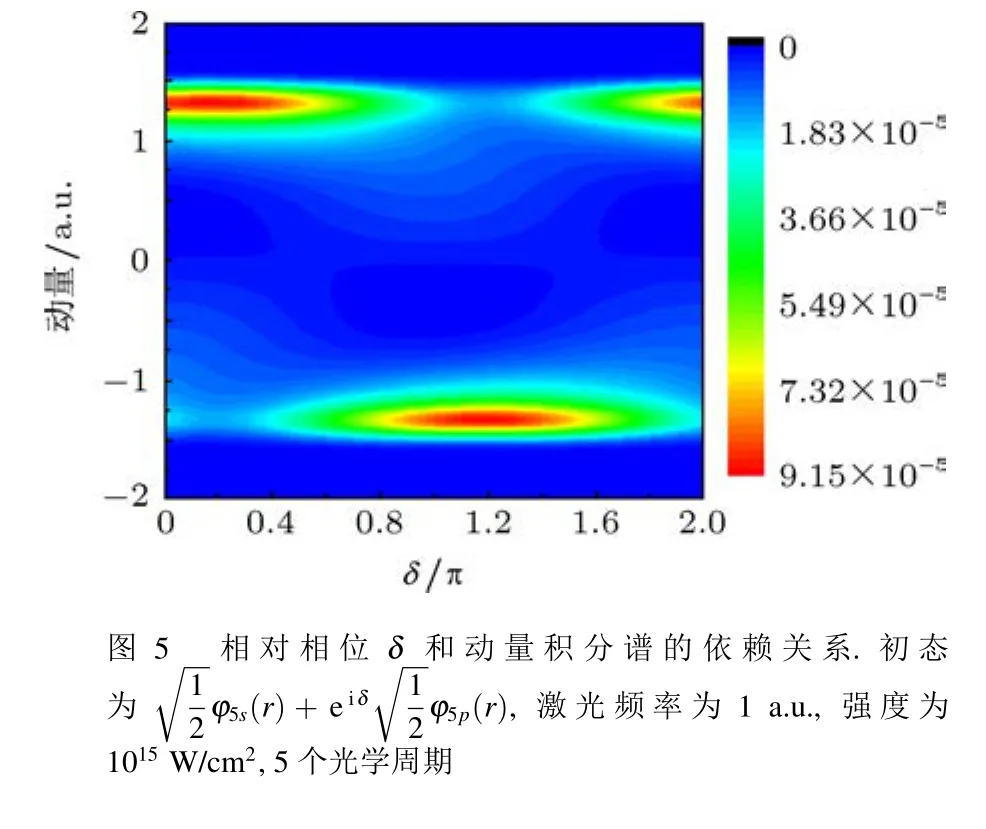
在对初态为纯态的结构识别基础上，还可以对体系初态为相干叠加态的原子进行识别.对于体系为叠加态的原子，由于是单电子过程，因此可以分析其ATI能谱信息，确定该光电子分别来源于哪一个n.同时计算不同分波的投影bl′(ε,t)，进而确定对应的初始叠加态中的l，同时还可以确定不同的权重信息.为了准确对体系初态为叠加态的原子结构识别，还需要给出叠加态之间的相对相位信息.为了确定叠加态相对相位，为此我们计算了不同初始相干态相位的光电子动量分布信息.选择的激光脉冲为5个光学周期，强度为5×1014W/cm2.选择的初态为5s和5p的叠加态：

计算结果表明：由于初态不再是纯态，其动量分布呈现出非对称结构.我们在动量空间，对x方向积分，得到在激光电场方向的光电子动量分布.通过改变两个激发态的相对相位，我们得到了对应的光电子发射谱的动量分布，如图5所示.从图中可以看出，随着相对相位的变化，动量分布的峰值从一侧转换到另一侧，因此可以在实验上通过探测不同方向动量的分布来探测叠加态中两个初态的相对相位.尽管本文的识别方案主要是针对原子的初态，但原则上可以将该方案推广到对分子结构的探测.

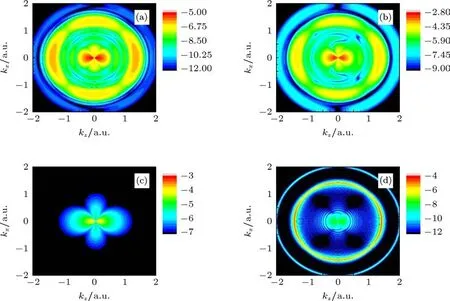
图4 初态为5p的光电子动量角度分布 (a)，(b)分别表示入射激光频率为1 a.u.，强度为1013W/cm2和1015W/cm2，5个光学周期;(c)，(d)分别表示脉冲持续时间为1和30个光学周期，强度为1013W/cm2

4 结论

本文基于含时伪谱方案在动量空间数值求解三维含时薛定谔方程，系统地研究了原子的激发态在高频激光脉冲作用下的光电离问题，给出了电离阈值附近的ATI光电子能谱和两维动量角分布.通过对ATI光电子能谱和两维动量谱的分析，可以分别确定体系初态的主量子数n和角量子数l，从而实现对原子初态的识别.对于体系初态为纯态的情形，光电子动量角度分布呈现的圆环规律特征不随入射激光脉冲强度和脉宽改变而改变;对于体系初态为叠加态情形，出现了有趣的非对称结构.通过改变叠加态的相对位相，相应的光电子动量角度分布的对称性也随之发生变化.值得指出的是，与通常采用HHG对初态波函数成像的方法不同(其中包含了电离电子的再散射过程)，本文提出的方法利用的是高频激光脉冲的直接电离过程，电离电子携带了初态波函数的信息.原则上讲，本方法的信息的提取更为准确和直接.

[1]Macklin J J，Kmetec J D，Gordon C L 1993 Phys.Rev.Lett.70 766

[2]Walker B，Sheehy B，DiMauroL F，AgostiniP，Schafer K J，Kulander K C 1994 Phys.Rev.Lett.73 1227

[3]Wang B B，LiX F，GaoL H，Fu P M，GuoD S，Freeman R R 2001 Chin.Phys.Lett.18 1199

[4]Cormier E，Garzella D，Breger P，AgostiniP，Cheriaux G，Leblanc C 2001 J.Phys.B 34 L9

[5]Becker W，Grasbon F，Kopold R，Milosevic D B，Paulus G G，Walther H 2002 Advances in Atomic,Molecular,and OpticalPhysics 48 35

[6]Grasbon F，Paulus G G，Walther H，VilloresiP，Sansone G，Stagira S，NisoliM，SilverstriS 2003 Phys.Rev.Lett.91 173003

[7]Armstrong G S J，Parker J S，Taylor K T 2011 New.J.Phys.13 013024[8]Paulus G G，Nicklich W，Xu H，Lambropoulos P，Walther H 1994 Phys.Rev.Lett.72 2851

[9]Toyota K，Tolstikhin O I，Morishita T，Watanabe S 2009 Phys.Rev.Lett.103 153003

[10]Telnov D A，Chu S I 2009 Phys.Rev.A 79 043421

[12]Tong X M，HinoK，Toshima N 2008 Phys.Rev.A 74 031405(R)

[13]KlingMF，RauschenbergerJ，VerhoefAJ，HasovicE，UphuesT，Milosevic D B，Muller H G，Vrakking M J J 2008 New.Journal.Phys.10 025024

[14]MeckelM，Comtois D，Zeidler D，Staudte A，Pavicic D，Bandulet H C，Pepin H，Kieffer J C，Dorner R，Villeneuve D M，Corkum P B 2008 Science 320 1478

[15]van der Zwan E V，Lein M 2012 Phys.Rev.Lett.108 043004

[16]EbadiH，KeitelC H，Hatsagortsyan 2011 Phys.Rev.A 83 063418

清华大学美术学院副教授蒋红斌“以设计思维为核心的企业创新组织”，从企业创新角度阐述了冰箱行业产品结构升级的必要性。他认为，设计思维来自于生活之美，而非生硬的技术，技术应该与生活对话，在使用中及时发现问题，以用户应用体验驱动行业创新，企业才能达到最佳的创新状态。

[17]EbadiH 2012 J.Opt.Soc.Am.B 29 2503

[18]Song Y，GuoF M，LiS Y，Chen J G，Zeng S L，Yang Y J 2012 Phys.Rev.A 86 033424

[19]Yang Y J，Chen J G，ChiF P，Zhu Q R，Zhang H X，Sun J Z 2007 Chin.Phys.Lett.24 1537

[20]Chen J G，Wang R Q，ZhaiZ，Chen J，Fu P M，Wang B B，Liu W M 2012 Phys.Rev.A 86 033417

[21]http：//hasylab.desy.de/facilities/ flash/， http：//lcls.slac.stanford.edu/，http：//www-xfel.spring8.or.jp/[2013-01-15]

[22]Goulielmakis E，Schultze M，Hofstetter M，Yakovlev V S，Gagnon J，Uiberacker M，Aquila A L，Gullikson E M，Attwood D T，Kienberger R，Krausz F，Kleineberg U 2008 Science 320 1614

[23]Chen J G，Yang Y J，Zeng S L，Liang H Q 2011 Phys.Rev.A 83 023401

[24]Zhou Z Y，Chu S I 2011 Phys.Rev.A 83 013405

[25]Landau R H 1983 Phys.Rev.C 27 2191

[26]Maung K M，Kahana D E，Norbury J W 1993 Phys.Rev.D 47 1182

[27]Norbury J W，Maung K M，Kahana D E 1994 Phys.Rev.A 50 2075

[28]Dionissopoulou S，Mercouris T，Lyras A，Nicolaides C A 1997 Phys.Rev.A 55 4397