场与非线性介质原子相互作用模型的量子纠缠动力学特性*
2013-02-25吕海艳侯喜文
吕海艳 袁 伟 侯喜文
(华中师范大学物理科学与技术学院,武汉 430079)
(2012年12月28日收到;2013年2月27日收到修改稿)
1 引言
由于量子纠缠在量子信息科学中起着非常重要的作用,人们提出了多种纠缠量度如约化Neumann熵,concurrence[1],和负性等[2].约化Neumann熵是通过计算子系统的约化密度矩阵得到,能很好的描述纯态的量子纠缠.对两量子比特,concurrence能用解析的数学公式计算[1],负性是计算部分转置密度矩阵的迹模[2].尽管它们的定义完全不同,但它们能很好地描述纠缠态的特性,特别是约化Neumann熵被广泛地用来研究场与原子相互作用系统[3]和其他模型[4-8]的量子纠缠动力学.
最近文献[9]给出来任意两组分量子态的concurrence,其优点是不仅考虑了密度矩阵的部分转置,而且还考虑了密度矩阵的重排.我们将利用文献[9]提出的concurrence来研究场与原子相互作用系统的纠缠动力学,并计算约化Neumann熵,发现concurrence与约化Neumann熵主要是正关联的.此外,在合适的模型参数与初态的条件下,量子纠缠在较长时间内具有几乎不变的特性,使得人们有足够的时间来完成量子信息处理.
2 模型
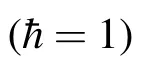

其中ω和ω0分别为场和原子的频率;a†和a是场的产生和湮没算符;b†和b是原子的产生和湮没算符;γ是非线性参数;g是场与原子的耦合参数.当原子处在基态与场处在光子相加相干态的直积为初始态,将模型参数固定为ω=ω0=1,γ=1,g=100,文献[3]研究了约化Neumann熵动力学.由于推广的二项式态能在实验中实现,还能用于量子门[10],我们将考虑场处在推广的二项式态和几组不同的模型参数γ和g,研究concurrence和约化Neumann熵的动力学.
3 纠缠动力学特性
我们选取场的初态为推广的二项式态,而原子的初态为基态,整个系统的初态为

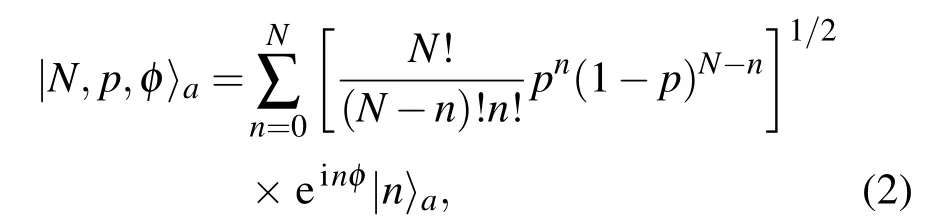
其中|N,p,φ〉a是推广的二项式态[10],N是光子数,0≤ p≤ 1,φ是相角,|n〉a是场的 Fock 态,|0〉b是原子的基态,下标a和b分别对应于场和原子子系统,初态的时间演化是 |ψ(t)〉=e-iHt|ψ(0)〉,相应的密度矩阵 ρ=|ψ(t)〉〈ψ(t)|.
我们利用两种纠缠量度来研究场与原子相互作用模型(1)的初态(2)的纠缠动力学.一种量度是concurrence,其定义[9]为

其中ρa=Trbρ是将密度矩阵对其中的一个子系统b求迹.

图 1 concurrence(实线)和约化 Neumann熵 (点线)的时间演化,其中γ =0.02((a),(c)); γ =0.25((b),(d));p=0.04((a),(b));p=0.5((c),(d))
我们还研究了其他模型参数和初态,以及较长的演化时间,发现上述两个结论还是适用的,图2是又一个例子.在图2中,g=1,p=1,γ =0.02((a),(c)); γ =0.25((b),(d));N=3((a),(b));N=6((c),(d))的 concurrence和约化 Neumann 熵.当 p=1时,推广是二项式态退化为Fock态|N〉a.从图2(a)可以看到,在弱非线性参数γ和低激发Fock态条件下,concurrence和约化Neumann熵几乎是等同的,且具有较好的准周期性.

图 2 concurrence(实线)和约化 Neumann 熵 (点线)的时间演化,其中 g=1,p=1:γ=0.02((a),(c));γ=0.25((b),(d));N=3((a),(b));N=6((c),(d))
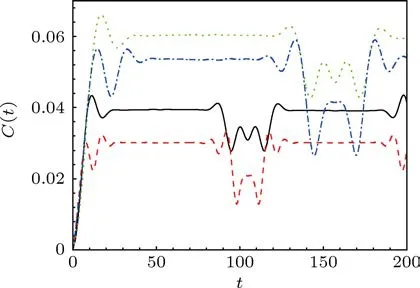
图3 concurrence的时间演化,其中参数γ=0.03,p=0.5,N=15(实线);γ=0.03,p=0.7,N=15(短虚线);γ=0.02,p=0.5,N=15(点虚线);γ=0.02,p=0.7,N=12(短点虚线)
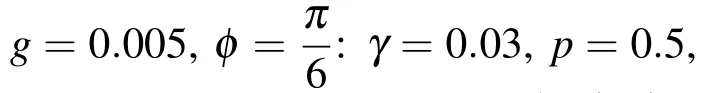
4 结论
我们研究了场与非线性介质中的原子相互作用系统的量子纠缠动力学,发现纠缠的两种量度concurrence和约化Neumann熵是正关联占优势;在适当的条件下,几乎不变的纠缠具有较长的时间.这有利于量子纠缠理论和量子信息.此外,我们可以探讨混态的纠缠特性,包括多组分量子纠缠,并考虑环境对纠缠的影响[16,17].
[1]Wootters K W 1998 Phys.Rev.Lett.80 2245
[2]VidalG,Werner F R 2002 Phys.Rev.A 65 032314
[3]Sudheesh C,Lakshmibala S,Balakrishnan V 2006 J.Phys.B 39 3345
[4]Hou X W,Cheng C M 2009 Chin.Phys.B 18 2719
[5]ZhaiL J,Zheng Y J,Ding S L 2012 Chin.Phys.B 21 070503
[6]QiL N,Zhang S 2009 Acta.Phys.Sin.58 4630(in Chinese)[齐琳娜,张寿2009物理学报58 4630]
[7]Xia J P,Ren X Z,Cong H L,Wang X W,He S 2012 Acta.Phys.Sin.61 014208(in Chinese)[夏建平,任学藻,从红璐,王旭文,贺树2012物理学报61 014208]
[8]CuiC C,Xie S Y,Yang Y P 2012 Acta.Phys.Sin.61 124206(in Chinese)[崔丛丛,谢双媛,羊亚平2012物理学报61 124206]
[9]Chen K,AlbeverioS,FeiS M 2005 Phys.Rev.Lett.95 040504
[10]FrancoR L,CompagnoG,Messina A,NapoliA 2012 Phys.Lett.A 374 2235
[11]Chen K,Wu L A 2002 Phys.Lett.A 306 14
[12]LiZ J,LiJ Q,Jin Y H,Nie Y H 2007 J.Phys.B 40 3401
[13]Hou X W,Chen J H,Wan M F,Ma Z Q 2008 Eur.Phys.J.D 49 37
[14]Hou X W,Wan M F,Ma Z Q 2009 Phys.Rev.A 79 022308
[15]Masanes L 2006 Phys.Rev.Lett.96 150501
[16]Hou X W,Wan M F,Ma Z Q 2012 Eur.Phys.J.D 66 152
[17]Hou X W,Wan M F,Ma Z Q 2012 Chin.Phys.B 21 103301
