Dy在Nd2Fe14B晶格中的占位及其对Fe原子磁矩影响的第一性原理计算*

郝红飞 王 静 孙 锋 张澜庭

(上海交通大学材料科学与工程学院，平野真一创新研究所，上海 200240)

(2012年10月18日收到;2013年1月29日收到修改稿)

1 引言

稀土永磁材料在各个领域都有着广泛的用途.钕铁硼作为第三代永磁材料，越来越多的被应用于电动汽车电机及风力发电电机之中[1].为获得高矫顽力的钕铁硼磁体，通常采用Dy合金化的方法[2]，但不可避免的会导致剩磁的下降.Dy在钕铁硼磁体中的合金化以Dy原子置换Nd2Fe14B硬磁相中Nd原子的方式进行，因此细致研究Dy在Nd2Fe14B晶胞中的优先占位，对理解Dy元素对钕铁硼磁体性能的影响规律有着重要意义.

由于Nd2Fe14B晶体结构的复杂性，基于密度泛函理论(DFT)的第一性原理计算成为了研究其电子结构以及磁性能的有效手段.从Nordstorm等[3]计算Nd2Fe14B中Fe的原子磁矩到Tanaka等[4]使用第一性原理研究并计算了Nd2Fe14B和Dy2Fe14B稀土原子的晶格场因子，对Nd2Fe14B化合物的物理本质有了深入认识.从组成元素考虑，影响Nd2Fe14B磁性能的因素有稀土元素[5]、过渡族金属元素[6]以及非金属元素[7]，其中对稀土元素的研究和关注最多.R2Fe14B(R：稀土元素)晶格中稀土元素的晶体学不等价的位置有两个：4f位和4g位，实验测量中可以看到其呈现了不同的磁矩.本文通过在Nd2Fe14B晶格中Nd的4f位和4g位上分别置换Dy原子的方式，研究了稀土原子Dy在Nd2Fe14B中的优先占位，以及掺杂对化合物中Fe原子磁矩的影响.

2 计算方法

2.1 计算参数

计算采用VASP5.2软件包(维亚纳从头计算模拟包，Vienna Ab-initioSimulation Package)，采用PAW-GGA对晶胞参数进行优化.使用自洽-自旋极化方法模拟体系的电子结构、磁性能及电荷密度.其中能量收敛判据为1×10-5eV/atom，取平面波的截断能为Ecut=415 eV，原子受力不超过0.02 eV/nm，第一布里渊区按5×4×3进行分格.考虑到稀土离子有比较大的轨道角动量[8]，为了估量自旋轨道耦合(SOI)的贡献，对Nd2Fe14B进行了SOI计算，并与自洽自旋极化方法进行了对照.

由于镧系金属4f电子的高度局域化特性，需将4f电子作为半芯态处理.在VASP的赝势中，对4f电子进行标准的局域处理，其中选取的Nd的赝势中3个4f电子为芯态，1个4f电子为价态，Dy的赝势中9个4f电子为芯态，1个4f电子为价态.由于4f电子无关键合作用，这种处理方式可以比较好的描述化合物的结合能与形成能.但在计算磁性性质的时候，自旋磁化密度4f态和它对价态的影响在计算中应予纳入，因此需要在计算中进行修正.引入描述类似Hartree-Fock类的库仑交互作用参数U(GGA+U)计算化合物的原子磁矩，根据文献报道[9,10]以及对三元系中的Fe原子磁矩的计算结果与实验对比，本文中在磁矩计算部分采用GGA+U的方式，皆选取U=6 eV.

2.2 晶胞结构的建立

R2Fe14B是四方结构，空间群P42/mnm.选取室温下的晶格常数构建初始晶胞，如图1，(Nd2Fe14B：a=b=0.8805 nm，c=1.2206 nm[11];Dy2Fe14B：a=b=0.8760 nm，c=1.2013 nm[12]).1×1×1的晶胞由4个R2Fe14B分子式组成，在一个晶胞内有68个原子，其中有8个R原子，56个Fe原子，4个B原子.R原子有两个不等价晶体学位置(4f，4g)，Fe原子有 6 个不等价晶体学位置 (4c，4e，8j1，8j2，16k1，16k2)，B原子有仅一个不等价晶体学位置(4f).

3 计算结果与讨论

3.1 结构研究

利用Murnaghan方程[13]对弛豫后晶胞体积优化和原子弛豫进行拟合，得到基态下Nd2Fe14B及Dy2Fe14B的平衡晶格常数，如表1.

经弛豫后，Nd2Fe14B的基态平衡晶格常数比实验值[11]分别低0.84%和0.90%，c/a值低0.07%;Dy2Fe14B的基态平衡晶格常数比实验值[12]分别低1.00%和1.29%，c/a值低0.29%.可知在计算中，基态平衡晶格常数与实验值非常接近.计算环境为绝对零度，实验值为室温下数据，可以解释计算值比实验值略低.同时对原子位置进行了充分的弛豫，晶胞内原子相对位置变化幅度小于0.09，可以推知建立的R2Fe14B晶格具有较好的结构稳定性.

表1 Nd2Fe14B和Dy2Fe14B的晶格弛豫结果

为研究Dy在Nd2Fe14B中的优先占位及其对磁性能影响，兼顾掺杂结构的晶格稳定性及实际应用的掺杂量，用Dy原子在Nd2Fe14B晶胞内部的(002)面上进行替换，分别替换(002)面4f位的一对Nd原子及4g位的一对Nd原子，掺杂浓度原子百分比为2.9%，相应的化学式为(Nd0.75Dy0.25)2Fe14B.

4 形成能及结构稳定性的研究

化合物的形成能是该化合物的总能量与各纯组元间的总能量差.对R2Fe14B可表达为

为计算各单质的总能量，对 Nd，Dy，Fe，B[14-17]纯组元的晶胞结构在相同的计算环境下进行弛豫，计算所得的总能量值如表2.相应可得Nd2Fe14B，Dy2Fe14B和(Nd0.75Dy0.25)2Fe14B的形成能及置换能，如表3.

形成能计算表明Dy2Fe14B比Nd2Fe14B形成能更低，与实验结果相符.Dy在Nd2Fe14B晶胞中掺杂的置换能为负值，表明Dy元素使R2Fe14B晶胞更加稳定.当Dy占据4f位时化合物的形成能较Nd2Fe14B降低了28.9%，置换能为-1.113 eV/unit.当Dy占据4g位时，形成能较Nd2Fe14B降低了24.9%，置换能为-0.959 eV/unit.说明Dy原子可自发进入Nd2Fe14B晶体置换Nd原子，并优先占据4f位.

表2 计算的各单质的总能

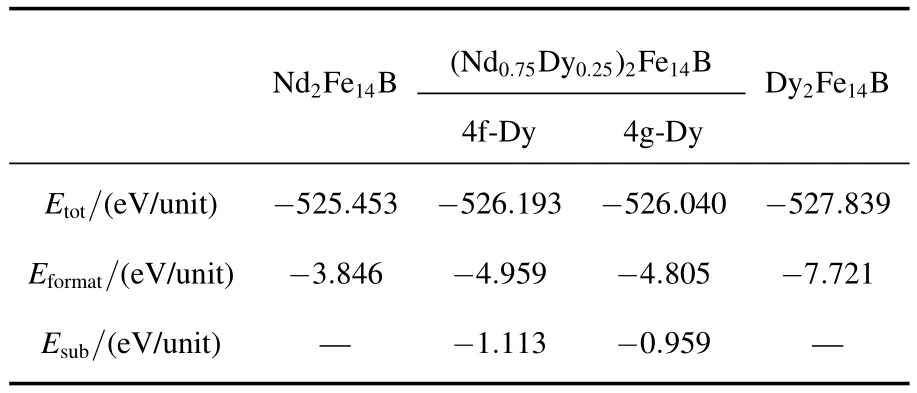
表3 三元及Dy掺杂(4f位和4g位)的R2Fe14B晶格的形成能

5 Dy掺杂对Fe原子磁矩的影响

在进行GGA+U修正计算后，R2Fe14B晶胞中各原子的磁矩如表4.

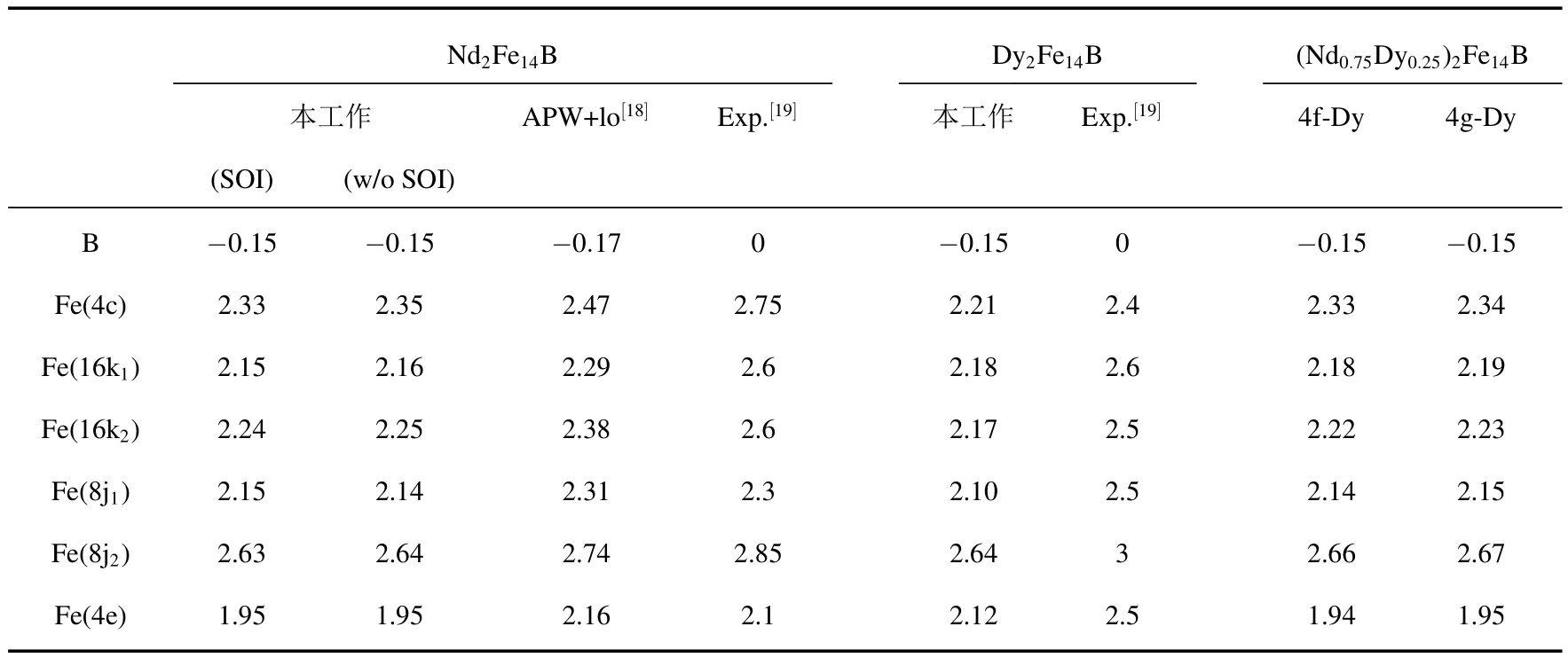
表4 三元及Dy掺杂(4f位和4g位)的R2Fe14B晶格的Fe原子磁矩计算结果及APW+lo[18]及实验值[19]的对照

与文献报道的实验值及缀加平面波加局域轨道(APW+lo)计算结果相比较，本文的计算结果与之符合很好.SOI的计算结果表示，轨道磁矩贡献不大，磁矩变化并不明显.这可能是由于在VASP的稀土元素的GGA势函数处理有关.考虑SOI计算所得的能量比自洽-自旋极化计算的要低(Etot=-527.973 eV).

所计算的化合物中，B的原子磁矩为-0.15µB/atom，对化合物总体磁矩基本无贡献.不同晶体占位的 Fe原子中，Fe(8j2)的磁矩均为最高，Fe(4c)和Fe(4e)均较低.对于Nd2Fe14B和Dy2Fe14B晶格中各原子磁矩分析可知，对R2Fe14B磁矩贡献最大的为Fe原子，且在Dy2Fe14B中，Fe的原子磁矩比Nd2Fe14B中均有一定程度的降低.与Nd2Fe14B相比，在Dy原子掺杂的(Nd0.75Dy0.25)2Fe14B晶格中Fe原子的磁矩值都呈降低趋势，相比占据4g位置的Dy原子，占据4f位置的Dy原子使Fe原子的磁矩有了进一步的下降.Nd2Fe14B和Dy2Fe14B单胞磁矩的实验值分别有报道为37.7µB/f.u.和11.3µB/f.u.[20].由于Dy原子倾向于首先占据4f位置，因此在低掺杂的情况下，对R2Fe14B磁矩的影响会更大一些.

(002)面上Dy原子的置换一定程度上破坏了Nd2Fe14B的晶格对称性，将晶胞内每个原子视为非等同原子进行分析.发现掺杂后(002)晶面周围的Fe原子的磁矩相对变化更大.在(Nd0.75Dy0.25)2Fe14B晶胞中，根据原子间距分析，在具有相同晶格占位(例如8j2位)的Fe原子中，与掺杂Dy原子距离在5.0以内的Fe原子磁矩值比与之间距大于5.0的Fe原子要低0.5%左右.这说明了稀土原子对Fe原子的磁矩影响与原子间距甚为密切.

通过电荷密度图，可以清晰地观察到R2Fe14B中的电子云分布.图2中的电荷密度图参数均为电荷密度最高为0.1个单位，最低为0，其中等高线密度为0.01单位.由图2在Nd2Fe14B和Dy2Fe14B电荷密度图中见：1)多数电荷都集中在Fe原子周围;2)Fe原子周围的电子云没有呈现出很好的球对称性，皆向B原子扭曲;3)稀土原子并未与Fe原子和B原子形成很强的共价键;4)B原子呈现了明显的各向异性，与周围原子呈现了明显的共价结构，说明B原子虽然对磁矩基本没有贡献，但是对形成R2Fe14B晶体结构起了重要作用[21,22].

由于Dy属于重稀土元素，在Dy2Fe14B中，Dy周围Fe原子电子云各向异性相比Nd2Fe14B要强，这与Tanaka研究相符[4].B作为R2Fe14B的骨架形成元素，图2中显示Fe与B在Dy2Fe14B中呈现了更强的共价键特性，这解释了在形成能计算值以及实验中观察到的Dy2Fe14B更加稳定的现象.

在R2Fe14B中，R-R以及R-Fe的原子间距都较远，因此4f电子云以及4f和3d电子云都不会重叠，而是通过传导电子为媒介产生间接交换作用，因此3d金属的自旋磁矩和4f金属的自旋磁矩总是反平行排列.根据Hund法则，在Nd2Fe14B等轻稀土化合物中，亚电子层中电子填充未达到半满，稀土金属的原子磁矩与4f金属的自旋方向相反，因此Fe的3d电子自旋磁矩与稀土金属原子磁矩是同向平行排列，即铁磁性耦合;而在Dy2Fe14B等重稀土化合物中，亚电子层中电子达到或超过半满，稀土金属的原子磁矩与4f金属的自旋方向相同，因此Fe的3d电子自旋磁矩和稀土原子磁矩是亚铁磁性耦合的.这解释了Dy原子周围的Fe原子磁矩比Nd原子周围低的原因.

图2 R2Fe14B(002)面的电荷密度图 (a)Nd2Fe14B;(b)Dy2Fe14B

在R2Fe14B中原子间距对磁性有很重要的影响[23]，在Nd2Fe14B中，4f位的Nd原子与Fe原子的距离平均为5.09，4g位的Nd原子与Fe原子的平均距离为5.77.在Dy2Fe14B中，4f位的Dy原子与Fe原子的距离平均为4.98，4g位的Dy原子与Fe原子的平均距离为5.67.4f位的稀土元素与Fe的距离更近，这可能是导致4f位稀土原子对周围Fe原子磁矩影响更大的因素.

6 结论

采用基于第一性原理投影缀加波和梯度矫正局域密度近似(PAW-GGA)，对Nd2Fe14B和Dy2Fe14B的基态晶格属性及Dy在Nd2Fe14B的掺杂进行了研究，并采用了GGA+U的修正方式对Dy掺杂对磁矩的影响做了研究：

1.Nd2Fe14B及Dy2Fe14B三元化合物的计算结果显示：Nd2Fe14B的形成能为-3.846 eV/unit;Dy2Fe14B的形成能为-7.721 eV/unit.Dy2Fe14B晶格比Nd2Fe14B晶格更加稳定.

2.4f位置换Dy原子的形成能比Nd2Fe14B纯晶胞降低了28.9%，置换能为-1.113 eV/unit.4g位置换Dy原子的形成能比Nd2Fe14B纯晶胞则降低了24.9%，置换能为-0.959 eV/unit.这表明Dy原子倾向于置换Nd2Fe14B中的Nd原子，并倾向于占据Nd2Fe14B晶胞中的4f位.

3.计算表明了Dy原子与周围Fe原子的耦合磁矩比Nd原子与Fe原子耦合磁矩低，并且计算结果显示，稀土原子在4f位上对Fe原子的磁矩影响更大，这可能与4f稀土原子与Fe原子距离较近有关.

感谢HIMI-Toyota合作项目对本研究的支持.

[1]Gut fleisch O，Willard M A，Brck E，Chen C H，Sankar S G，Liu J P 2011 Adv.Mater.23 821

[2]Matsuura Y 2006 J.Magn.Magn.Mater.303 344

[3]Nordstrom L，Johansson B，Brooks M S S 1993 J.Phys.：Condens.Matter.5 7859

[4]Tanaka S，Moriya H，Tsuchiura H，Sakuma A，DiviM，Novk P 2011 J.Appl.Phys.109 07A702

[5]Zhu Y，ZhaoT，Jin H，Yang F，Xie J，LiX，ZhaoR，de Boer F R 1989 IEEE Tran.on Mag.25 3443

[6]Wang H Y，ZhaoF A，Chen N X，Liu G 2005 J.Magn.Magn.Mater.295 219

[7]SuiY C，Zhang Z D，Liu W，XiaoQ F，ZhaoT，ZhaoX G，Chuang Y C 1997 J.Magn.Magn.Mater.172 285

[8]Jiang S T，LiW 2003 Condensed matter magnetic physics(Beijing：Science Press)p225(in Chinese)[姜寿亭，李卫2003凝聚态磁性物理(北京：科学出版社)第225页]

[9]HiroshiM，HirokiT，Akimasa S 2009 J.Appl.Phys.105 07A740

[10]Loschen C，CarrascoJ，Neyman M K，Illas F 2007 Phys.Rev.B 75 035115

[11]Herbest J F，Croat J J，Yelon W B 1985 J.Appl.Phys.8 57

[12]Herbst J F，Yelon W B 1985 J.Appl.Phys.57 2343

[13]Murnaghan F D 1944 Proc.Natl.Acad.Sci.USA 30 244

[14]Lundin C E，YamamotoA S，Nachman J F 1965 Acta Metall.13 149

[15]Morozkin A V 2002 J.Alloys Compd.345 155

[16]Giles P M，Longenbach M H，Marder A R 1971 J.Appl.Phys.42 4290

[17]Switendick A C，Morosin B 1991 AIP Conf.Proc.231 205

[18]Tanaka S，Moriya H，Tsuchiura H，Sakuma A，DiviM，Nov’ak P 2011 J.Phys.：Condens.Matter.266 012045

[19]Zhou S Z，Dong Q F 2004 Sintered NdFeB rare earth permanent magnet materials and technology(Beijing：MetallurgicalIndustry Press)p138(in Chinese)[周寿增，董清飞2004烧结钕铁硼稀土永磁材料与技术(北京：冶金工业出版社)第138页]

[20]Hirosawa S，Matsuura Y，YamamotoH，Fujimura S，Sagawa M，YamauchiH 1986 J.Appl.Phys.59 873

[21]Ching W Y，Gu Z Q 1987 J.Appl.Phys.61 3718

[22]Gu Z Q，Ching W Y 1987 Phys.Rev.B 36 8530

[23]Tanaka S，Moriya H，Tsuchiura H，Sakuma A，DiviM，Novk P 2011 J.Phys.：Conf.Ser.266 012045