2013年福建物理高考22题第（3）问的特殊解法

张洪明

（宁波市北仑区明港高级中学，浙江 宁波 315800）

题目.（2013年福建试卷第22题）如图1（甲），空间存在一范围足够大的垂直于xOy平面向外的匀强磁场，磁感应强度大小为B.让质量为m，电荷量为q（q＞0）的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向入射到该磁场中，不计重力和粒子间的影响.求：

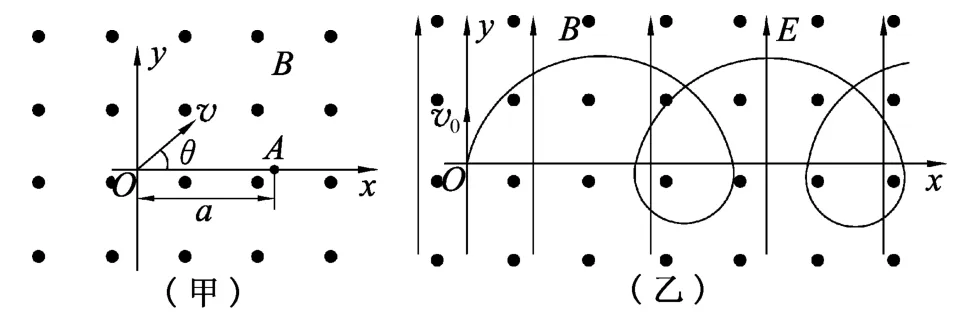
图1

（1）若粒子以初速度v1沿y轴正向入射，恰好能经过x轴上的A（a，0）点，求v1的大小；

（2）已知粒子的初速度大小为v（v＞v1）.为使该粒子能经过A（a，0）点，其入射角θ（粒子初速度与x轴正向的夹角）有几个？并求出对应的sinθ值；

（3）如图（乙），若在此空间再加入沿y轴正向、大小为E的匀强电场，一粒子从O点以初速度v0沿y轴正向发射.研究表明：粒子在xOy平面内做周期性运动，且在任一时刻，粒子速度的x分量vx与其所在位置的y坐标成正比，比例系数与场强大小E无关.求该粒子运动过程中的最大速度值vm.

解析：第（1）、（2）问解法从略.

解法1：功能关系和特殊值法相结合.

粒子在电场与磁场复合场里运动，只有电场力做功，根据粒子速度沿x轴分量vx与其所在位置的总坐标y成正比，如图1所示，当粒子的纵坐标最大的时也就是x分量vx最大.由动能定理得

点评：解决第（3）问关键点有：（1）要想到洛伦兹力不做功，并应用动能定理来解决问题，电场力做功特点与路径无关W＝q E d；（2）要想到将题中信息“粒子速度的x分量vx与其所在位置的y坐标成正比”这句话转换为方程vx＝k y；（3）要将“比例系数与场强大小E无关”这句话理解，想到用给出的信息既然k与E无关，可以假设E＝0变成匀速圆周运动来解决.第（3）问对学生分析综合能力要求非常高，是选拔优秀学生的好题.

解法2：配速法.

沿着x轴的正方向与负方向附加一对等大反向的速度v和－v，这样叠加以后等效为初始条件没有变化.另由v所产生的洛伦兹力为

图2

这样粒子所受的合力就等效为由速度为

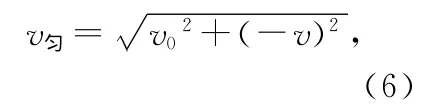
图3

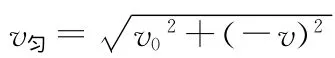
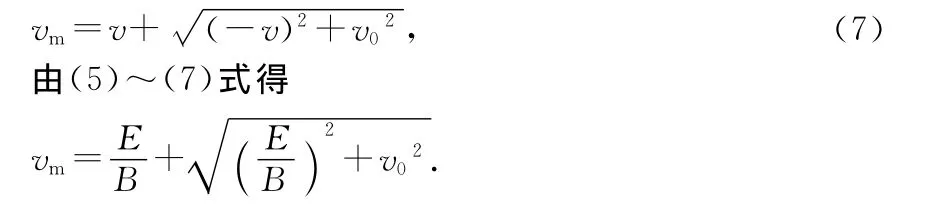
与解法1结果相同，证明解法2是正确的.

评析：第（3）问的问题实际与2011年福建省高考22题是类似的，粒子的实际运动模型是摆线运动，只要是在恒力与洛伦兹力合力作用下的运动，粒子的合运动只存在3种可能：（1）恒力与洛伦兹力平衡，粒子做匀速直线运动；（2）除了洛伦兹力以外其他力的合力为0（即恒力为0），粒子做匀速圆周运动；（3）恒力不为0也不与洛伦兹力平衡，粒子运动是匀速直线运动与匀速圆周运动的合成（即摆线运动）.以上第（3）种情况都可以用以上的配速法（也叫0速度分解法）进行解答.