运用平面几何知识巧解物理问题

刘成华

（江苏省前黄高级中学，江苏 常州 213161）

物理教与学的过程都离不开数学知识和方法的应用，借助物理知识渗透考查数学能力是高考命题的永恒主题，平面几何知识是在物理教学过程中是应用较广泛的数学知识之一.应用几何方法求解物理问题时，常用到的有“对称点的性质”、“平行四边形对角线互相平分”、“直角三角形中斜边大于直角边”以及“全等、相似三角形的特性”等相关几何知识.

1 运用平行四边形性质巧解物理问题

两组对边分别平行的四边形叫做平行四边形.有时解决物理问题可以运用平行四边形的性质：① 平行四边形两组对边分别平行且相等；② 平行四边形的两组对角分别相等；③ 平行四边形的对角线互相平分等.

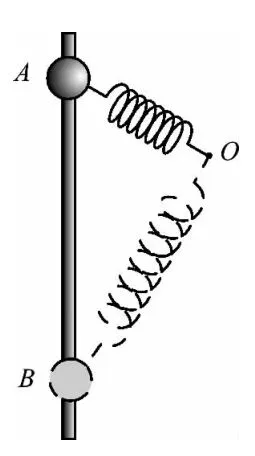
图1

例1.如图1所示，一质量为m的小球套在光滑竖直杆上，轻质弹簧一端固定于O点，另一端与该小球相连.现将小球从A点由静止释放，沿竖直杆运动到B点，已

知OA长度小于OB长度，弹簧处于OA、OB两位置时弹力大小相等.在小球由A到B的过程中

（A）加速度等于重力加速度g的位置有两个.

（B）弹簧弹力的功率为零的位置有两个.

（C）弹簧弹力对小球所做的正功等于小球克服弹簧弹力所做的功.

（D）弹簧弹力做正功过程中小球运动的距离等于小球克服弹簧弹力做功过程中小球运动的距离.

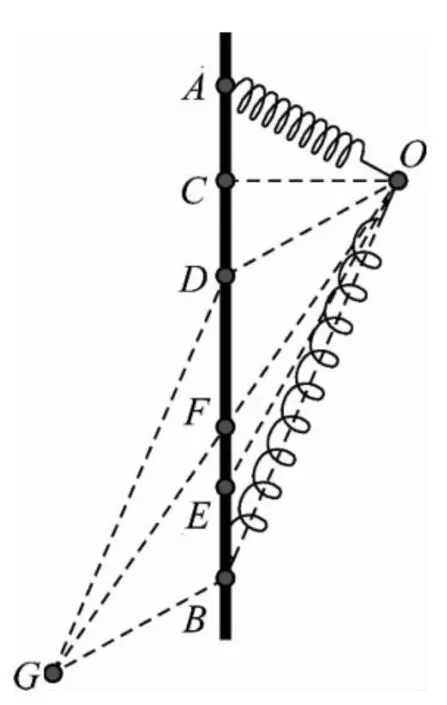
图2

解析：如图2所示，取OC⊥AB，O E＝l0（l0为弹簧原长）.小球在C、E两处的加速度等于重力加速度g，小球在A、C、E3处功率为0，故（A）正确（B）错误；小球处于A处时，弹簧被压缩，处于B处时弹簧被拉长，OA的压缩量等于OB的伸长量，即小球在A、B两位置弹簧的弹性势能相等，故（C）正确.

本题关键在于弹力对小球做正功与负功的过程中小球运动距离大小的判断，小球由A到C过程中弹力做负功，由C到E的过程中弹力做正功，由E到B的过程中弹力做负功，即是比较AC＋EB与CE的大小.在AB杆上取关于OC对称的D点，因AC＝CD，则只要比较DE与EB的大小.由题意可知，lOD＝l0－x，lOB＝l0＋x，过D、B分别作OB、OD的平行线交于G点，构造平行四边形ODGB，连接OG交DB于F点，由平行四边形对边相等且对角线互相平分的知识可得DF＝FB，lOB＋lBG＞lOG＝2lOF，而lOB＋lBG＝2l0，即lOF＜l0，而lOE＝l0，则弹簧原长点E应该在F 点下方，又因为DF＝FB，不难得出DE＞EB，故题中选项（D）是错误的.

解决本题时巧妙地运用了平行四边形对边相等及对角线互相平分的性质.再如江苏省的一道高考题也可运用此类方法.

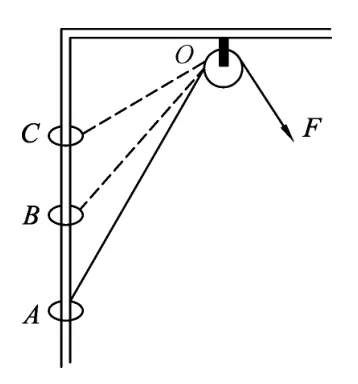
图3

例2.如图3所示，固定的光滑竖直杆上套着一个滑块，用轻绳系着滑块绕过光滑的定滑轮，以大小恒定的拉力F拉绳，使滑块从A点起由静止开始上升.若从A点上升至B点和从B点上升至C点的过程中拉力F做的功分别为W1、W2，滑块经B、C两点时的动能分别为EkB、EkC，图3中AB＝BC，则一定有

（A）W1＞W2. （B）W1＜W2.

（C）EkB＞EkC. （D）EkB＜EkC.

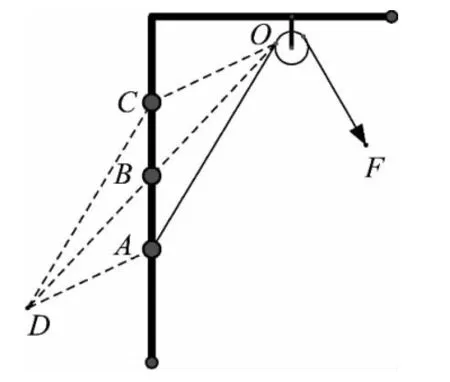
图4

解析：如图3所示，滑块从A点上升至B点和从B点上升至C点的过程中拉力F作用点的位移大小分别为（OA－OB）和（OB－OC），则W1＝F（OA－OB），W2＝F（OBOC）.过A、C分别作OC、OA的平行线交于D点，则四边形OADC为平行四边形，如图4所示，由平行四边形性质得：OB＝BD、AB＝BC.在△OAD中有OA＋AD＞OD，因AD＝OC，OB＝BD则有OA＋OC＞2OB，即OAOB＞OB－OC，得W1＞W2，故选项（A）正确.

由于滑块在A点由静止出发，可以肯定最初滑块是加速上升的，也就是说刚开始绳对滑块拉力的竖直分力要大于滑块的重力，但由于绳对滑块拉力的竖直分力是逐渐减小的，B到C的过程绳对滑块拉力的竖直分力与重力的大小关系不清楚，所以滑块的运动可能是加速的，也可能是减速的，还可能是先加速后减速的，所以无法确定滑块在B、C位置的动能大小，故选项（C）、（D）错误.

2 运用相似三角形性质巧解物理问题

对应角相等、对应边成比例的两个三角形叫做相似三角形.有时解决物理问题可以运用相似三角形的一些性质：① 对应角相等；② 对应边成比例；③ 对应的垂线、中线、角平分线成比例.

例3.一个重为G的小环套在竖直放置的半径为R的光滑大圆环上，一个劲度系数为k，原长为l0（l0＜2R）的轻弹簧，一端固定在大圆顶点A，另一端与小环相连，小环在大圆环上无摩擦滑动，小环静止于B点时，如图5所示，求弹簧与竖直方向的夹角θ.

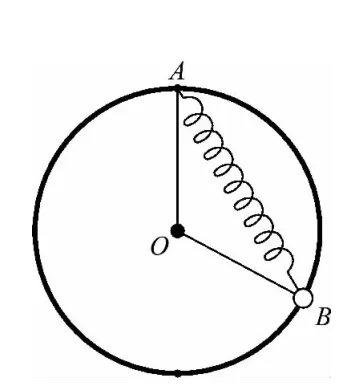
图5

图6

在对物体受力分析过程中，若各力之间没有特殊角度但边长关系知道的情况下，可以考虑运用相似三角形的性质来解决，再如下一个动态平衡问题.

例4.如图7所示，在半径为R的光滑半球面上高h处悬挂一定滑轮，重力为G的小球用绕过滑轮的绳子被站在地面上的人拉住.人拉动绳子使小球在与球面相切的某点缓缓运动，到接近顶点的过程中，试分析小球对半球面的压力和绳子拉力如何变化（小球可以看着质点）.

图7

图8

解析：受力分析如图8所示，依然可以依据相似三角形性质解决本题，分析过程不再赘述，不难得出：压力N不变、拉力T逐渐变小.

3 运用圆的几何性质巧解物理问题

有时解决物理问题可以运用圆的性质，例如：① 垂直于弦的直径平分这条弦，并且平分弦所对的弧；② 直径所对的圆周角是直角；③ 圆的切线垂直于过切点的直径等等.

图9

例5.在共点力合成的实验中橡皮筋一端固定于P点，另一端连接两个弹簧秤，并使该端拉至O点，两个弹簧秤的拉力分别为F1、F2（α＋β＜90°），如图9所示.现使F2大小不变地沿顺时针转过某一角度，要使结点仍在O处，相应地使F1的大小及图中β角发生变化.则相应的变化是

（A）F1一定增大. （B）F1可能减少.

（C）β角一定减小. （D）β角可能增大.

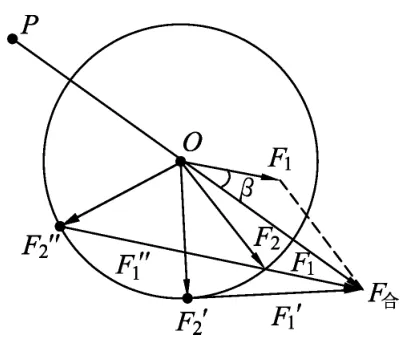
图10

解析：由于F2大小不变，则可以运用圆的性质来解决本题.以O点为圆心，F2的长度为半径画圆，如图10所示，F2在沿顺时针方向转动过程中，合力的大小、方向不变，两个分力与合力构成一个矢量三角形，在转到图中F2′的位置（此时F1与圆相切，即F1′⊥F2′）过程中，β角增大到最大，F1增大，继续转到图中F2″的位置，β角减小到与原来相等，F1继续增大，可见F2绕O点顺时针转动过程中，F1一直增大，而β角是先增大后减小，故选项（A）、（D）正确.

例6.一条宽度为d的河，水流速度为为v水，已知船在静水中的航速v船，那么（1）怎样渡河时间最短？（2）若v水＜v船，怎样渡河位移最小？（3）若v水＞v船，怎样渡河船漂向下游的距离最短？

解析：（1）、（2）两问比较简单，这里不再赘述；对于（3）问v水＞v船，不论船的航向如何，总要被水冲向下游，怎样才能使船的航程最短呢？如图11所示，设船头（v船）与河岸成θ角，合速度（v）与河岸成α角，可以看出：α角越大，船到下游的距离x越短.那么，在什么条件下α角最大呢？

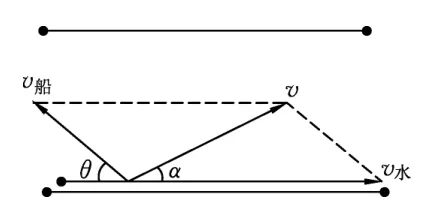
图11

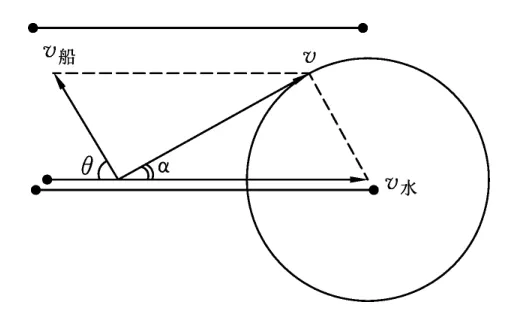
图12

高中物理教学中离不开平面几何知识，特别是物体的平衡问题、运动的合成与分解、带电粒子在电磁场中的运动、光的反射折射等问题，都常会用到平面几何知识，故我们在求解有关问题时如能确当运用平面几何知识往往会收到意想不到的效果.