城市群一体化与政府互动的多智能体模拟

罗 杭

（清华大学 公共管理学院，北京100084）

一、引 言

统筹区域经济建设、促进地区协调发展是我国社会经济发展的重要目标。改革开放以来，我国先后提出鼓励东部地区率先发展、推进西部大开发、振兴东北等老工业基地、促进中部崛起等一系列区域发展战略。当前我国区域统筹发展也面临了新的机遇：一方面，为创新地方社会经济发展，提升区域竞争力，国务院自2005年起相继批复了10个国家级综合配套改革试验区，如武汉城市圈、长株潭城市群“两型社会”试验区等；另一方面，不少经济发达地区也出现了基于经济集聚的区域自发合作现象，如长三角城市群、珠三角城市群和环渤海湾京津冀都市圈区域合作等。这些改革试验区或经济合作区横跨多个行政市乃至多个省，在实现协作治理和区域一体化进程中，面临着一系列问题和挑战：区域内各城市不存在直接的行政隶属关系，各自享有独立的行政权，难以协同合作；区域内各城市经济社会发展水平不一致（如武汉城市圈“强市弱圈”、京津冀都市圈“环京津贫困带”），一体化收益并不均衡，难以形成政策共识；区域内各城市以自身利益和短期利益为出发点，忽视集体利益和长远利益，“各自为政”、“恶性竞争”，易陷入发展的困境。事实上，任何一种改革，无论是政治、经济、社会层面的改革，都难免受到部分利益群体消极心理和行为的抵制。城市群一体化作为一种全方位、深层次、系统性的区域性变革尤其如此，并非所有城市都能成为一体化的当期利得者，利失者往往对一体化改革持保留或反对态度，并直接或间接、显性或隐性地阻挠一体化进程。因此，有必要分析城市群一体化进程中各城市政府决策主体的心理及行为，了解他们接受一体化的心理感知程度，并为上层政府或协调机构促进城市群一体化进程提供决策依据和参考。

国内外相关学者从城市群一体化的合作模式、协调机制、困境成因、对策建议等方面展开了一系列研究［1］［1］［2］［3］［4］［5］［6］［7］，但主要属于定性研究，或部分静态、单期、线性的定量研究。然而，城市群多政府互动是一个动态演变、异质构成、自组织、自适应的复杂系统，由多个具有独立行政权力和独自利益诉求的城市政府主体构成。面对区域内的共同社会经济事务，他们在相互沟通的基础上不断互动、反复博弈、相互影响，力求实现主体之间的协同效应，以及多主体与周围环境、整体目标之间的相互适应。受制于有限理性和信息的不完全性，各主体在特定时空条件下仅受有限范围内其他主体的影响，宏观系统的整体行为通过微观个体之间的局部交互而涌现出来，并呈现出不确定性、多态均衡、非线性结构等特征。基于城市群多政府互动的特定机理，现有研究（包括定性研究和传统的数学建模等）往往难以有效解释，因此，有必要借鉴复杂性科学理论，应用多智能体建模与仿真技术，构建一个城市群一体化多政府互动仿真模型，从一种超脱还原论的、自底向上的、微观互动到宏观涌现的视角，动态、持续地模拟城市群各政府主体的行为互动过程与偏好演化机理，并通过可视化界面呈现和统计分析演化中的规律和涌现出的现象，为上层政府或协调机构促进城市群一体化进程提供决策依据和政策参考。

二、模型构建

1.系统运行机理分析

当前我国城市群多政府协商的主要制度化框架是各类型的联席会议，如武汉城市圈联席会议、长三角城市群经济协调会、京津冀区域合作高端会议等。城市群联席会议是一种不同于传统垂直型领导模式的横向府际协同框架，各城市决策者不存在直接的行政隶属关系，基于平等的原则，对区域内共同社会经济问题表达立场、交流沟通、互动博弈。当前的城市群一体化改革主要包含区域经济协调发展、生产要素自由流动、公共服务一体化等议题，主要涉及经济发展和社会管理领域。因此，各城市政府官员在互动过程中不仅仅考虑行政权力（各自的行政层级），也更多考虑经济实力（各城市的经济发展水平）和一体化的实际收益。

基于城市群经济社会发展水平的非均衡性，一体化变革往往给各城市带来不同的利益得失，使得作为理性决策者的城市政府官员对一体化持或高或低的支持态度。并且，一体化偏好并不是一成不变的，而是受到外界环境的影响而不断演化，因为个体存在于社会中，其心理和行为必然受到群体和环境的影响而发生改变［8］，称之为群体压力。在政府系统中，群体压力产生的影响尤其明显，例如，当某一决策者的政策偏好与大部分群体成员相异时，为了维护自己与群体成员的关系，避免得罪其他“同僚”、被组织孤立以及丧失自己的政治前途等，该主体往往不会“固执己见”、“针锋相对”，而是会在强大的心理压力下向群体靠拢、与组织趋同。

群体压力受利益得失、行政权力、经济实力等因素的共同影响。利益得失决定了群体压力作用的方向，行政权力和经济实力则决定了群体压力的大小。如果一体化收益为正，则该主体塑造赞成一体化的群体压力；如果一体化收益为负，则自然形成反对一体化的群体压力。较大的行政权力和经济实力意味着更大话语权和影响力。以武汉城市圈为例，尽管联席会议中的各城市政府代表不存在直接的行政隶属关系，但武汉市作为省会城市与唯一副省级市，其市长的政策态度对群体的影响无疑要远大于仙桃、天门、潜江等省辖县级市；同样，在协商市场一体化、产业承接互补等经济领域问题时，武汉作为区域内具有绝对优势的最大经济体，无疑有更大的影响力。对于每一个决策主体，其交互范围内赞成和反对一体化的双方会各自形成方向相反、力量各异的群体压力，若赞成势力大于反对势力，则该主体支持一体化程度提升，反之下降。总之，利得者和利失者在互动过程中为了维护各自利益而展开角力，力求让群体一体化偏好向有利于自身的方向演化发展。

2.建立概念模型

在运用多智能体系统模拟政府群体行为互动与态度演化方面，吴江和胡斌进行了较为成熟的研究。他们以信息化改革为例，构建了一个政府信息化群体行为模型EGGBM，模拟群体压力对政府成员信息化接受程度的动态影响［9］。本文结合城市群多政府互动的特定机理，借鉴EGGBM模型，并加以改进：（1）引入经济实力变量；（2）引入方案类型变量，作为利益得失与经济实力之间关系的调节变量（正相关或负相关）；（3）设计新的变量关系，分别建立原变量行政权力、新变量经济实力与利益得失之间的联系。

在此基础上，构建本模型的因果关系图（见图1），基于系统、联系、发展的观点，将城市群多政府主体互动视为一个包括输入、内部构造、输出和反馈的大系统：（1）输入包括设定主体属性初始值和相关环境系数；（2）内部构造是由一个个智能体（agent）组成的相互作用的人工社会组织［10］，其利益得失、经济实力和行政权力三个关键变量共同塑造了群体压力；（3）输出是各主体的一体化偏好；（4）反馈是输出对上层政府或协调机构的调控手段产生的影响，以武汉城市圈为例，上层政府即湖北省政府，协调机构包括国家层面发改委的“国家促进中部地区崛起工作办公室”、省层面是湖北省政府的“省推进武汉城市圈建设领导小组办公室”等。

具体分析三个核心变量利益得失、经济实力、行政权力之间的内部联系：（1）行政权力和利益得失之间存在正相关性，行政权力较大的城市拥有更大的话语权和影响力，能使政策方案的制定和实施向有利于自己的方向演变；（2）经济实力和利益得失之间也存在相关性，但受到一体化具体方案的调节，呈正相关性或负相关性。例如，对于市场一体化，经济实力强、拥有众多优势企业的城市往往持赞成态度，因为它们能够享受到市场全面开放带来的经济收益与税收增长，而经济实力弱、缺乏优势企业的城市则往往持反对态度，奉行地方保护主义。因此，市场一体化往往对经济实力较强的城市更有利。而对于社会保障一体化，则一般对经济实力较弱的城市更有利，因为经济发达、城市人口占比大的城市往往不愿意与经济落后、农业人口占比大的城市共享社会保障储蓄，共同分配社会保障资金。此外，利益得失、行政权力和经济实力这三个主体属性变量也受其他变量的影响：（1）激励措施会影响主体收益，但受到价值观类型的调节，只有当激励类型与主体价值观类型匹配时才能发挥效用，可以按照Sprauger的理论，分为经济、社会和政治型三类价值观［11］；（2）行政权力的初始分配由行政权力层级、组织结构惯性等决定，并在系统演化过程中受行政措施的持续影响。组织结构惯性越大，组织权力等级越森严，不同层级之间的权力差别就越大；（3）经济实力的分配由经济实力层级、经济层级系数等决定。

图1 概念模型的因果关系图

3.建立数学模型

基于有限理性和信息的不完全性，群体压力对主体行为和态度的影响都是局部性的，在特定时空环境下，决策主体仅受可交互范围内（界定为邻居域内）有限其他主体的影响。本文设定Moore型邻居域为主体交互范围，与Von Neuman型邻居域相比有更广阔的邻域范围，能更好地反映电子政务和移动政务模式下的政府工作环境。伴随着电子政务和移动政务的推广和普及，借助计算机网络、移动通信等信息技术，政府之间的沟通与协作更加方便快捷、随时随地，信息获取更加充分，交互范围更加广泛［12］。如图2所示，用中心黑色方框表示某一智能体，周围灰色方框表示其邻居域，该智能体的下一刻状态由此智能体及其邻居域内其他智能体的当前状态基于局部规则运算得出。函数表达为f（sti，stN），其中为第i个智能体的当前状态为邻居域（neighbour）内其他智能体的状态组合。

图2 Von Neuman与Moore邻域比较

其设计规则1～7如下，其中规则1、2为初始变量设置规则，规则3～7为循环执行。

规则1 首先设定各城市行政权力，以武汉城市圈9市为例，有省会城市即副省级城市1个（武汉）、地级市5个（咸宁、黄石、黄冈、孝感和鄂州）、县级省直辖市3个（仙桃、天门和潜江），因此，9市的行政权力共可分为三级。设P为行政权力，In为组织结构惯性，le为行政层级，各层级主体行政权力表示为Ple，其中，le＝｛1，2，3｝。为简化模型，将最高行政权力P′赋值为1，各层级主体行政权力之间的关系为：

规则2 评定各城市经济实力较为复杂，可以用一个相对系统、全面的指标即GDP。为方便数据处理，不直接采用GDP原始数据作为经济实力系数，而是基于GDP数值和特定的运算规则对各城市的经济实力分等定级。以武汉城市圈2010年数据为例，武汉市GDP达5565.93亿，远远高于其他8市，处于第一层级，而黄冈、孝感、黄石3市的GDP基本位于700～900亿元一档，处于第二层级，此外，咸宁、鄂州、仙桃、潜江、天门5市的GDP大体位于200～500亿元一档，处于第三层级［13］。设E为经济实力，Co为经济层级系数，le为经济层级，其中le＝｛1，2，3｝。为简化模型，将最强经济实力E′赋值为1，则各层级主体经济实力之间的关系为：

规则3 行政措施压制利失者（反对者）的行政权力，以遏制反对一体化的阻力。设行政措施为AM（t），主体收益为B（i）（t），随指数α1衰减（调控效果具有生命周期），则有：

规则4 激励措施提升相同价值观类型主体对一体化的收益。设激励措施强度为SM（t），类型为TypeSM，随指数α2衰减，价值观类型为Value（i），则有：

规则5 较大的行政权力（大于平均值）提高主体收益，幅度取决于权力引致利益递增系数PIBI；而较小的行政权力（小于平均值）降低收益，幅度取决于权力引致利益递减系数PIBD，随指数α3衰减，则有：

规则6 经济实力对利益得失的作用方式受一体化方案属性Plan的调节，令Plan＝0时呈正相关性，Plan＝1时呈负相关。设经济引致利益递增系数EIBI和经济引致利益递减系数EIBD随指数α4衰减，则有：

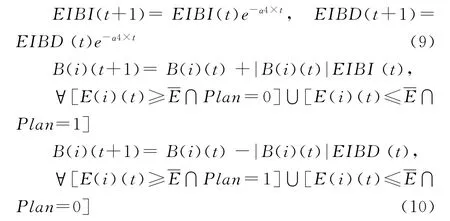
规则7 对于各智能体 其Moore邻域内的利得者和利失者将分别塑造赞成一体化和反对一体化的势力（设为FS和FO），双方进行相互博弈，合力形成群体压力（设为Pr）。设决策主体支持一体化程度为SID（i）（t），则SID（i）（t）＝｛x｜0≤x≤1｝，值为1表示该主体完全赞成一体化，值为0表示该主体完全反对一体化。

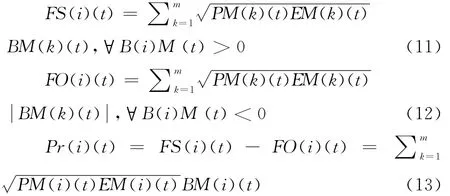
其中，m表示Moore邻域内其他Agent数量。

4.建立计算机模型

关于多智能体模拟系统的开发，有Swarm、Repast、Ascape、AnyLogic、Matlab等平台可供选择，其中Netlogo是目前较先进的模拟软件之一，具有较强的可扩展性和友好的可视界面，因此，本文选取Netlogo作为多智能体模拟系统的实现工具。

三、模型验证

本文涉及的社会模拟存在大量定性数据和半结构数据，且实证获取困难，要用完全定量、实证的方法验证“模型能够映射真实世界”是不可能的［14］。因此，本文应用定性验证方法［15］，参考胡斌和蒋国银的模拟系统验证框架［16］：设计朴素的模型验证实验方案；模拟运行得到相应输出；将输入－输出与常识比较，如果输入－输出符合常识，则模型有效，否则无效。设计两套验证实验如下：

1.第1套验证实验

考察城市群各决策主体中利得者和利失者的不同构成对一体化偏好的持续影响。以武汉城市圈9市为例设计3个方案，设定利得者数目分别为0、5、9，保持其他所有变量一致（其中，SID初始均值皆为0.5），不施加行政措施和激励措施。

实验结果如下，图3显示了3个方案在t＝0及t＝200时刻各主体支持一体化程度的微观分布状态，图4为3个方案中0～200时SID均值演化图（例如，t＝200时的SID值由图3映衬得出）。方案1的SID均值迅速、稳定地下降至0（t＝81），方案3的SID均值则快速、稳定地上升至1（t＝20），方案2的SID均值则有一定幅度的反复波动，终值为0.73。分析原因，方案1各主体皆为利失者，势必合力形成反对一体化的群体压力，使得SID不断下降；而在方案3各主体皆为利得者，群体相互影响的结果必然使得SID不断上升；方案2为方案1和方案3的折中方案，利得者和利失者“势均力敌”，皆不具备对群体全局的绝对影响力和控制力，因而易出现“反复争夺”的局面，使得SID均值线反复波动。分析表明，以上三组实验方案的演示结果基本反映了客观规律，与常识相符。

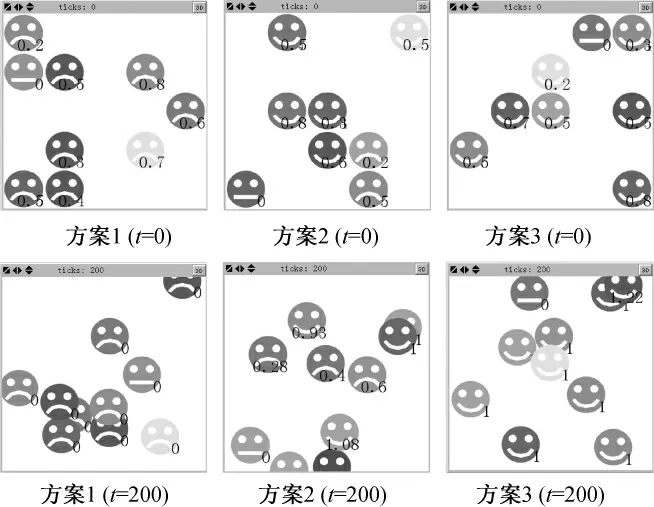
图3 方案1、2、3在时间t＝0及t＝200时刻群体一体化偏好分布

图4 方案1、2、3的群体支持一体化程度均值演化

2.第2套验证实验

考察激励措施类型与价值观类型的匹配程度对调控效果的影响。设计2个方案，设定2／3为政治人，1／6为社会人，1／6为经济人，保持其他变量不变，其中方案1施加政治型激励措施，方案2施加经济型激励措施。方案1的SID均值由0.5上升至0.78，方案2的SID均值由0.5上升至0.66，前者显著高于后者，群体支持一体化程度更高。模拟实验结果与常识相符，只有根据主体的价值观构成施加相应类型的激励措施，即“对症下药”，才能发挥较好的调控效果。由此，本模型通过了两个朴素实验方案的检验，基本符合常识与客观规律，能够较好地映射现实系统。

四、模型应用

在检验模型基础上，进行模拟实验研究，考察不同强度的行政措施、不同类型的激励措施对一体化偏好的持续影响，以及预测不同初始状态下的未来演化趋势。通过实验条件控制下的计算机赋值获取变量数据（严格控制变量的“变”与“不变”，构建近似于自然科学的严格实验环境），以演示应用模拟系统获取预测结果和提供决策参考的具体操作流程，并探究系统演化的一般性。在具体案例的实证研究中，可以通过调研收集实地数据（如通过问卷调查、访谈法评估政府主体的政策偏好、利益得失，利用“奥尔波特－弗农－林德西价值观研究法”测量主体的价值观类型等［11］），输入模拟仿真平台获取更有针对性和指导意义的决策参考。

1.第1套模拟实验：选择适当强度的行政措施

为提升群体支持一体化程度，上层政府或协调机构可采取行政措施，以压制反对者的行政权力，削弱影响势力。考察不同强度（0、0.3、0.5、0.7、1）的行政措施对SID演变的持续影响，辅助挑选最合适的行政措施，既要有较好的引导效果（使SID均值在180～200时段接近1），又具有较小的强度（行政措施本身具有执行成本，且过高强度的行政措施可能产生负面影响，使演化结果过度偏离于自然均衡）。

实验结果如图5所示，方案1在20≤t≤200时段始终波动于0.6～0.7区间，终值为0.64；方案2在0≤t≤40时段稳定上升，随后大幅波动，终值为0.90；方案3在0≤t≤100时段持续上升，终值为0.95；方案4在t＝65时上升为1，随后微幅波动，终值为0.99；方案5在t＝71时上升为1，随后保持不变，稳定于1。结果表明，随着调控强度的加大，反对者势力被抑制的程度越来越大，群体SID更加明显和稳定的趋向于1（即完全赞成一体化）。在180≤t≤200时段方案4和方案5的SID均值都稳定的接近最大值1，但方案4的强度为0.7，方案5为1，前者比后者的强度（成本）更小，具有较好的成本／收益比，为最适宜方案。

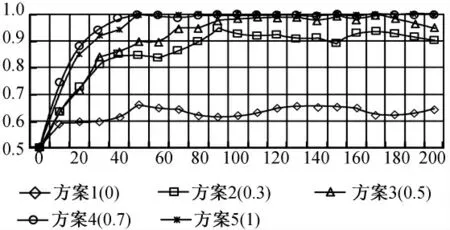
图5 方案1～5的SID均值变化

2.第2套模拟实验：选择适当类型和强度的激励措施

为提升群体一体化偏好，上层政府或协调机构也可采取激励措施。本文设计激励措施类型和强度分别不同的9组方案（P为政治型、S为社会型、E为经济型），保持其他变量不变，展开实验模拟，辅助管理者挑选最合适的激励措施，既要有较好的引导效果，又具有较小的强度／成本，因为激励措施本身会消耗资源，且过高强度的激励措施不利于群体形成自组织、自优化秩序。

实验结果如图6所示，考察180≤t≤200时段SID均值的演化趋势，方案1（P：0.2）、7（E：0.2）、8（E：0.5）的SID变化基本位于刻度线0.62之下，可首先排除；方案5（S：0.5）、6（S：0.8）的SID变化始终不超过刻度线0.64，也可排除；方案2（P：0.5）、3（P：0.8）、4（S：0.2）、9（E：0.8）的SID最高值皆超过0.65，且大部分时段位于刻度线0.62之上，相较其他方案具有更好的激励引导效果。其中，方案2是强度为0.5的政治型激励措施，方案3是强度为0.8的政治型激励措施，方案4是强度为0.2的社会型激励措施，方案9是强度为0.8的经济型激励措施，同时考虑成本因素，方案4为最佳选择。进一步，比较实验1和实验2的模拟结果发现，行政措施对SID的引导效果要明显高于激励措施，5组行政措施实验方案中有4组的SID结果都接近于1，而9组激励措施实验方案的结果皆不超过0.66。

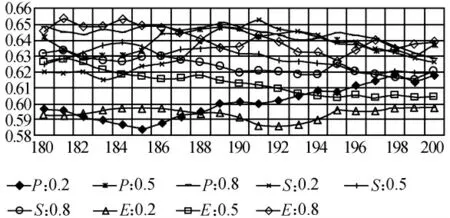
图6 方案1～5的SID均值变化

3.第3套模拟实验：预测一体化偏好的未来演变趋势

当上层政府或协调机构掌握了城市群政府主体的初始状态数据时，希望预测支持一体化程度的未来演变趋势，以便更有针对性地、及时准确地采取相应调控措施。设计3套实验方案，调整SID初始均值分别为0.2、0.5、0.8，保持其他所有变量不变，观察和比较不同方案在不同时点的一体化偏好演化态势。

实验结果如图7所示，无论初始状态如何，群体一体化偏好都会经历若干次波动后趋于一个稳定值。方案1初始均值为0.2，快速、稳定上升，t≥179后稳定于0.67～0.69区间，终值为0.69；方案2初始均值为0.5，大体保持上升趋势，t≥96后稳定于0.72～0.77区间，终值为0.73；方案3初始均值为0.8，基本保持稳定，微幅于0.8上下，终值为0.79。结果表明，虽然方案1、2、3中群体支持一体化程度的初始均值差距显著（0.2，0.5，0.8），但演化的最终结果差距很小（0.69、0.73、0.79），趋于一致。

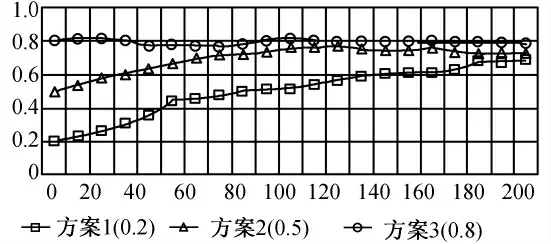
图7 方案1、2、3的均值变化

五、结论与建议

本文通过概念模型、数学模型和计算机模型的完整建模过程，建立一个城市群多政府互动仿真模型，系统思考并模拟实验了利益得失、经济实力、行政权力、群体压力等关键变量对群体一体化偏好的动态影响。研究结论与建议如下：

（1）无论初始参数如何调整，群体一体化偏好的演化结果总会趋向于稳定。根据组织行为学原理，群体成员在外部环境变化或内部相互作用下，总是从一种态度或行为的波动状态逐渐达到一种稳定的均衡状态。在城市群政府互动过程中，赞成和反对一体化双方“相互角力”、“反复争夺”，但互动结果总会趋于稳定，且很可能停滞于“非理想状态”。上层政府或协调机构应当准确判断和把握系统当前状态，在均衡格局出现之前及时采取调控措施，引导互动结果向有利的方向演变。

（2）相同强度的行政措施比激励措施的引导调控效果更加有效。行政措施的作用面更广，能压缩每一个利失者的行政权力和影响势力，而激励措施的作用范围仅限于价值观类型匹配的部分决策主体。上层政府或协调机构多样化、系统性的调控手段可向行政措施适当倾斜，以谋求较高的调节效率，这也符合于现实政治和行政系统的客观规律，对政府主体来说，强制性的行政手段往往比激励手段更加直接、有效。

（3）群体支持一体化程度的初始状态对未来演化结果没有决定性影响，上层政府或协调机构推进城市群一体化进程中，不能因为初始状态不理想而“却步”，应当全面、系统地考虑群体互动过程中的重要环节和关键因素，如利益分配、权力体系、经济格局等，并有针对性地采取合理的调控手段，提高决策主体的一体化收益，遏制反对势力的一体化阻力，促进区域统筹发展和城市群一体化进程。

［1］JESUS S，JOSE P，JORGE I.Intermunicipal cooperation：the effect of the metropolitan police in the almatam metropolitan area［J］.Gestion Y Politica Publica，2011，20（2）：433－457.

［2］HELLMUT W.Comparing two logics of interlocal cooperation：the cases of france and germany［J］.Urban Affairs Review，2010，46（2）：263－292.

［3］FEIOCK C，LEE I，JUN P.Collaboration networks among local elected officials：information，commitment，and risk aversion［J］.Urban Affairs Review，2010，46（2）：241－262.

［4］SAGER F.Policy coordination in the european metropolis：a meta－analysis［J］.West European Politics，2006，29（3）：433－460.

［5］LAQUIAN A.Metropolitan governance reform in Asia［J］.Public Administration and Development，2005，25（4）：307－315.

［6］陈群元，喻定权.中国城市群的协调机制与对策［J］.现代城市研究，2011，（3）：79－82.

［7］付景涛.“两型社会”建设主体的合作博弈研究——以长株潭城市群为例［J］.经济问题探索，2010，（9）：157－161.

［8］胡斌，董升平.管理者－人群心理归顺博弈定性模拟原理［J］.系统仿真学报，2004，（12）：2813－2816.

［9］吴江，胡斌.信息化与群体行为互动的多智能体模拟［J］.系统工程学报，2009，24（2）：218－225.

［10］张江，李学伟.人工社会——基于Agent的社会学仿真［J］.系统工程，2005，23（1）：13－20.

［11］HODGETTS R M.现代工作中的人际关系：第8版［M］.谢铮，郭悦译.北京：中信出版社，2005.120－156.

［12］罗杭，郭珍，张毅.移动政务的价值分析［J］.情报资料工作，2010，（4）：36－40.

［13］湖北省统计局.湖北统计年鉴2011［M］.北京：中国统计出版社，2011.

［14］BARLAS Y.Formal aspects of model validity and validation in system dynamics models［J］.Systems Dynamic Review，1996，12（3）：183－210.

［15］DIJKUM C D.Validation of Simulation Models［M］.Amsterdam：SISWO Publication，1999.102－130.

［16］胡斌，蒋国银.管理系统集成模拟原理与应用［M］.北京：高等教育出版社，2010.82－85.