环境振动试验传感器布置优化方法研究
2013-02-13李奇志陈国平
李奇志,陈国平,房 凯
(1.南京航空航天大学 振动工程研究所,南京 211006;2.南京电子技术研究所,南京 210039;3.中国人民解放军驻十四所军事代表室,南京 210039)
随着大推力电动振动台的出现,使得电子设备整机振动环境模拟试验得以实现。在试验过程中,整机夹具的尺寸有时远大于振动台台面尺寸,这将会导致试品振动输入各点响应加速度均方根值偏离设置的参考谱值,同时也会出现控制超差现象,严重情况甚至出现试验中断。为了解决这些问题,试验人员常采用多点布置控制传感器的方法,虽有学者胡小弟、周桐等[1-2]在试验和研究过程中发现通过改变控制传感器不同位置,可以改善夹具传递特性和控制特性,但未提出一套可行性的理论。美军标MIL-STD-810G[3]指出振动环境的产生和测量精度在很大程度上取决于夹具及试验样品的固定、测量系统和激励器控制策略,细致的设计试验、夹具、传感器安放位置在振动试验控制中是有必要的。同时,提出在振动试验的传统方法——输入控制中,控制加速度计安放在夹具与试品的连接点上,激励器的运动由控制加速度计的反馈来控制,在可行的情况下,控制信号可以是一个以上的试验样品/夹具传感器信号的平均值。但在实际试验过程中,虽然控制谱与输入的参考谱一致,但各控制点加速度均方根值相差很大,最大和最小的比值有时能达到2倍以上,这就出现试验输入严重不均匀和偏离设置参考谱的加速度均方根值的现象。
为了解决这种输入严重不均匀和偏离设置的参考谱加速度均方根值的现象,本文首先分析电动振动台多点控制原理和夹具传递函数特性,建立了在多点控制情况下基于响应加速度均方偏离度最小的传感器布置位置优化计算模型,然后,依据Patran和Nastran有限元软件计算某试品夹具的传递函数,通过Matlab仿真寻找传感器最优布置点,最后通过某试品夹具在控制传感器优化布置和传统布置二种情况下振动试验,比较二种传感器布置模式下试品与夹具连接点处响应均方加速度偏离度,从而证明本文所提传感器布置优化方法是实用和可行的。
1 数学模型的建立
1.1 电动振动台振动控制理论
如图1所示,振动试验是一种反馈控制的试验。当功放给定的推力与传感器检测到加速度信号满足试验需求时,即控制响应谱(加速度谱密度测量值)和参考谱(加速度谱密度设定值)一致时试验处于平衡状态,即:φ(f)参考谱=φc(f)控制响应谱,振动试验得以正常运行。

图1 振动台控制示意图Fig.1 Vibration control schematic diagram
当在多点控制时,一般振动控制信号有三种设置方式:平均控制、最大值控制、最小值控制,通常采用平均控制方式,即:

式中:φck(fp)为各控制传感器ck在频率fp上响应加速度谱密度测量值,k为控制点个数。
当φ(fp)参考谱=φc(fp)控制响应谱振动达到平衡,试验得以进行,即:

1.2 响应均方偏离度定义
当试品在振动台上试验时,在各频率分辨率点上控制输入谱为φ(fp)参考谱,夹具与产品的连接点上加速度谱密度响应谱(简称传递响应谱)为Φdi(fp),则定义[3]udz为总响应均方偏离度:

式中:i为夹具安放产品传递振动量级位置的个数,p为参考谱的频率,dv为频率段下限值,uv为上限值。
对于单点,则定义uds为为夹具与安放产品传递部位的单个振动响应均方偏离度:

由上两式可以看出当响应均方偏离度越大则表示传递给试品的振动量级与设置参考谱偏离越大,越不符合试验要求。
1.3 夹具振动传递特性[4]
由图1可知振动环境试验系统包括:振动台(含台体)、夹具、试品和控制仪器等。以夹具为研究对象,假定振动台传递给夹具的响应点位于振动台面的中心位置上的夹具o点,夹具传递给试品的响应为试品与夹具的安装部位di(i=1,2,….m),控制传感器安装位置为ck(k=1,2,….n),则由动力学分析知:

当考虑夹具上的受力部位o点,试品安装部位di及传感器安装位置ck,则有:

若在正弦激励作用下,由上式可得:

式中:Hodi、Hock为di、ck点相对于o点位移传递函数。
若是随机激励作用下,通过响应与激励协方差函数Fourier变换可得加速度功率谱密度传递函数等式:

式中:H(f)odi和H(f)ock分别为di和ck处相对于o点加速度功率谱密度传递函数,Φdi(f)和Φck(f)分别为di和ck处加速度谱密度,Φo(f)为o点振动台传递给夹具的加速度谱密度。
1.4 传感器布置优化模型
通过以上理论分析可知,当夹具尺寸较大,为了满足试验过程中控制特性,通常采用多点控制,这时夹具与试品的连接部位处传递给试品的响应会出现与参考谱不一致的现象而且各传递部位处响应也不一致,它是夹具的传递特性和振动台控制方式耦合的结果,基于以上思想,引入上文定义的响应均方偏离度最小的方法,建立表征传力点处的响应加速度谱密度与实际设定参考谱的加速度谱密度的函数F,则目标函数为:

将式(11)代入式(2)可得:

考虑实际试验过程中响应谱是分段频率测量的,所以有:

将式(13)代入式(10)可得:

所以目标函数为:

式中:SC为传感器可布置区域,当ck(k=1,2,….n)的位置满足上式目标函数,即是所求最优布置点。在di位置确定,SC区域明确时,可以编程将SC区域内所有可能的n点(将n点看成一个组)的传递函数值代入式(15)计算F值,通过比较所有的F值,最小F值对应的n点即是最优布置点ck。
2 实例
本文以某试品环境振动试验夹具为例,给定夹具与试品的连接部位,通过已建立优化模型计算加速度传感器最优布置位置。
2.1 传递函数的计算
本文以Patran和Nastran软件作为夹具传递函数计算平台,物理模型如图2,去掉对传递函数值影响不大的夹具棱边和倒角,所得有限元模型如图3,采用垂向振动方向作为传感器布置优化求解振动方向,固定约束夹具与振动台连接孔边界节点所有自由度,如图3所示。在10~2 000 Hz内取100个频率点、结构阻尼值设为0.02计算夹具与试品的连接部位和传感器可布置区域内节点的频率响应函数值,考虑到对称性和计算效率,夹具与试品的连接部位为图4中圆点所示位置节点、传感器可布置区域为图5中小四边形所示位置节点。
2.2 控制传感器最优位置计算
通过vc编程提取NASTRAN频响分析完成后的f06文件中夹具传感器可布置点位置节点和夹具与试品的连接部位节点相对于固定位置的传递函数值,最后依据优化模型,通过Matlab软件编程求得2个传感器最优布置为节点位置Node 62 485、84 005,如图6中圆点所示位置。

图2 物理模型Fig.2 Physical model

图3 有限元模型和约束部位Fig.3 Finite element model and the binding site

图4 夹具与试品的连接部位节点Fig.4 Clamp and sample connection node

图5 控制传感器可布置区域Fig.5 Control sensor arrangement area

图6 两控制传感器最优布置点Fig.6 The two control optimal sensor placement points

图7 控制传感器最优布置点试验图Fig.7 Optimal control sensor placement test chart
2.3 试验验证
本文以优化后控制传感器布置位置和传统的控制传感器布置位置分别在振动台上以10~2 000 Hz频率范围内以平直加速度谱密度0.001 623 18 g2/Hz,加速度均方根值为1.789 9g设置的参考谱做振动试验,振动物理试验如图7、图8所示,图中圆点所示位置为控制传感器布置点,夹具与试品的连接部位的位置Node 62 796、70 892、71 298、71 690的测试响应谱分别为图9中的input(5)~input(8)所示,加速度均方根值和各点及总的响应均方偏离度见表1。

图8 控制传感器传统布置点试验图Fig.8 Traditional control sensor placement test chart
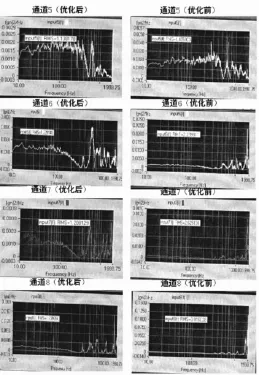
图9 优化前后夹具与试品连接点响应谱图比较Fig.9 Before and after the optimization of fixture and test connection point response spectrum comparison
从表1可以看出控制传感器优化布置后的加速度均方根值,input(5)~input(8)点的加速度均方根值最大与最小差值为0.7 g,总均方偏离度为0.012 087,传统布置input(5)~input(8)点的加速度均方根值最大与最小差值为1.37 g,总均方偏离度为0.706 85,由此可见优化后传感器布置所得夹具与试品的连接部位总均方偏离度远小于传统的传感器布置所得夹具与试品的连接部位总均方偏离度,由此可说明优化方案是可行、合理的。

表1 夹具与试品的连接部位测试点加速度均方根值和均方偏离度Tab.1 Fixture and test the connection part of test point acceleration root-mean-square value and mean square deviation
3 结论
本文首先对电动振动台多点控制反馈理论进行描述,结合试品在振动台上振动传递特性,建立传感器优化布置模型,然后以某产品的夹具为例,建立有限元模型,依据Nastran软件计算出夹具各点相对于振动台上固定位置的传递函数值,根据建立的优化模型,求出传感器最优布置位置,最后通过振动台振动试验,表明传感器放于最优布置位置所得夹具与试品的连接部位的响应总均方偏离度远低于传统的凭经验布置传感器的振动传递点的总均方偏离度,这也说明本文所用传感器优化布置方法是可行的和有效的,可以为其它环境试验传感器布置和试验方案的制定提供实践和理论指导。
[1]胡小弟,朱伟繁.用多点振动控制的方法优化夹具动态特性的研究[J].环境技术,1999,1:11-19.
HU Xiao-di,ZHU Wei-fan.Study on optimizing the dynamic characteristics of the fixture with the method of multipoint control[J].Environmental Technology,1999,1:47-51.
[2]周 桐,张思箭,李 健,等.夹具特性与振动控制方式对试件响应的影响[J].振动测试与诊断,2007,27(1):58-61.
ZHOU Tong, ZHANG Si-jian, LI Jian, et al. Fixture characteristic and vibration control method on response for the specimen[J].Vibration,Mesurement & Diagnosis,2007,27(1):58-61.
[3] MIL-STD-810G .Environmental Engineer Considerations and Laboratory Test,2010.
[4]高贵福,赵保平.一种定量评价随机振动试验效果的新方法——计量法[J].装备环境工程,2006,3(1):67-69.
GAO Gui-fu,ZHAO Bao-ping.A new method of describing the quantity of the random vibration test effect-statistics variable method[J]. Equipment Environment Engineering,2006,3(1):67-69.
[5]欧进萍,王光运.结构随机振动[M].北京:高等教育出版社,1998.
[6] Nastran2004 Quick Reference Guide[M].MSC,2003.
[7]胡志强,法庆衍,洪宝林,等.随机振动试验应用技术[M].北京:中国计量出版社,1996.
