考虑多间隙的齿轮柔性转子耦合系统非线性动力学分析
2013-02-13宋晓光郑建荣
崔 立,宋晓光,郑建荣
(华东理工大学 机械与动力工程学院,上海 200237)
齿轮轴承转子系统是在各种机械设备中都有广泛的应用,由于现代机械传动设备的要求越来越高,工作环境也开始向高速、高温、重载方向发展,对于齿轮转子系统的研究也就变得越来越重要。
目前对于齿轮非线性动力学进行了大量的研究,但是在齿轮轴承转子耦合系统方面的研究还不够成熟[1]。传统的研究方法往往忽略了整个系统的耦合作用,考虑自由度较少,将轴和轴承当做刚性体处理,未考虑柔性转子造成的响应或是将支承轴承简化成线性力,未考虑非线性轴承力的影响。如Kahraman等[2]考虑时变啮合刚度和齿侧间隙,建立了齿轮系统的动力学模型,但仅考虑3个自由度。李润方等[3]建立了弯扭耦合的齿轮系统力学数学模型,采用集中质量法,将支撑刚度设为定值,但未考虑轴、轴承对整个系统的影响。张锁怀等[4]建立了具有齿侧间隙的齿轮系统动力学模型,但转轴为刚性轴,系统仅考虑4个自由度。也有研究考虑系统多个自由度,考虑齿轮啮合产生的弯曲和扭转耦合振动,但往往忽略系统中的多种非线性因素及柔性转轴的影响[5-6]。
最近的研究开始考虑多种非线性因素耦合效应建模,比如Cai等[7-8]在建立齿轮轴承系统数学模型时,考虑了系统的强非线性因素,引入了非线性油膜力、非线性啮合力,这种模型得到了轴承、主动轮、被动轮中心点的振动响应时异步的。Byrtus[9]使用模态综合法建立了齿轮系统动力学模型,将时变啮合刚度、齿侧间隙、非线性轴承力等因素引入系统模型中,但未研究柔性转轴的影响。崔亚辉等[10-11]在建立齿轮模型过程中,考虑齿侧间隙、时变啮合刚度、静态传动误差、不平衡质量的影响。陈思雨等[12]建立了考虑齿侧间隙、时变啮合刚度齿轮模型,研究了齿轮非线性冲击响应,对脱齿现象进行了研究。李明等[13]研究了齿轮转子轴承系统的弯扭耦合振动和非线性动力学进展情况,提出应考虑多种激励同时作用下系统的动力学分析、同时考虑多种非线性因素的齿轮转子轴承系统动力学分析。蒋庆磊等[14]研究了齿轮传动多转子耦合系统振动特性,得到了齿轮副耦合作用对机组振动特性的影响。窦唯等[15]建立了高速齿轮转子系统弯扭耦合振动模型,研究了偏心距、齿轮啮合刚度等参数对系统振动响应的影响规律。但以上研究均未考虑滚动轴承的非线性振动影响。滚动轴承径向间隙引起的非线性现象也可导致转子系统失稳或进入混沌运动[16-17]。齿轮轴承转子系统是一个多自由度、多耦合、多间隙的非线性振动问题,需要考虑齿侧间隙、轴承径向间隙等多间隙的非线性因素。
本文考虑齿侧间隙、轴承径向间隙,考虑齿轮时变啮合刚度、轴承时变刚度,建立适用于复杂载荷的齿轮轴承柔性转子耦合的动力学模型,研究转速变化对齿轮系统动力学响应的影响、转轴刚度变化对系统动态特性的影响规律、齿侧间隙和轴承径向间隙变化对系统混沌运动的影响,提高齿轮转子系统的可靠性。
1 计算模型
首先建立齿轮副啮合模型和动力学模型;然后推导滚动轴承接触力的非线性模型;接着采用有限单元法将转子系统划分为弹性轴段、圆盘及支承,建立各节点的动力学模型;将各节点参数叠加,得到整个系统的动力学模型。
1.1 齿轮啮合模型
1.1.1 时变刚度激励
齿轮啮合传动过程中,齿根处啮合时弹性变形较小,齿顶处时弹性变形较大,因此啮合刚度随时间发生周期性变化。计算啮合刚度研究比较成熟的方法有石川公式、保角映射法、傅里叶级数展开法等。本文采用修正的梅泽清彦公式计算啮合线上每点的时变刚度[18],齿轮副的啮合综合刚度计算如下:


式中:km(t)为齿轮副啮合综合刚度;kp为节点处单对齿的啮合刚度;t为啮合时间;tz为端平面内转过一个基节的啮合时间;ε、εα分别为总重合度系数和端平面内重合度系数;b为有效齿宽;H为齿轮全齿高;q1~q5是由最小二乘法得到的常数,q1=-0.008 54,q2=-0.116 54,q3=2.978 4,q4=-0.006 35,q5=0.005 29;zv1、zv2为当量齿数;γ1、γ2为齿高修正系数。计算得到齿轮啮合时变刚度如图1所示,综合啮合刚度是一条连续的周期性曲线,这将造成齿轮在啮合过程中周期性振动。
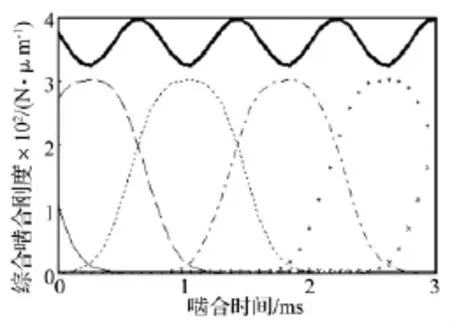
图1 齿轮啮合刚度Fig.1 Meshing stiffness for gear pairs
1.1.2 齿侧间隙激励
齿轮系统的受力分析如图2所示,沿y、z轴方向的齿轮动态啮合力分别通过Fy、Fz表示。
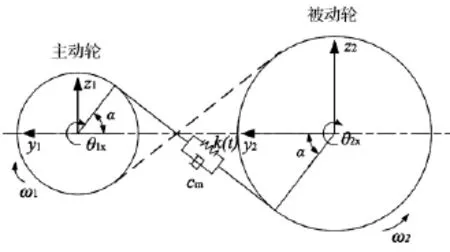
图2 齿轮啮合模型Fig.2 Model of gear mesh
轮齿的啮合传动会使其产生弯曲和扭转振动,考虑齿轮弯扭耦合的3自由度模型,齿轮中心处位移可表示为:
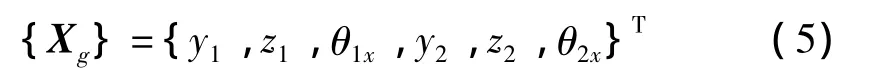
两齿轮在啮合线上的相对位移:
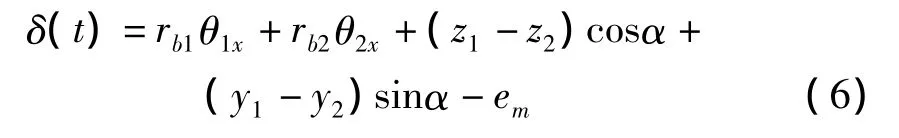
式中:em表示由于实际齿廓偏离理论位置引起的齿轮静态传动误差,α为齿轮压力角。
当δ(t)>bn时,齿轮处于正常啮合状态;当-bn<δ(t)<bn时,齿轮啮合会出现瞬时脱齿现象;当δ(t)<-bn时,出现齿背接触现象。
设齿侧间隙为2bn,采用分段函数表示齿侧间隙。轮齿间啮合力包括弹性力和阻尼力,可将时变啮合力表示为[19]:
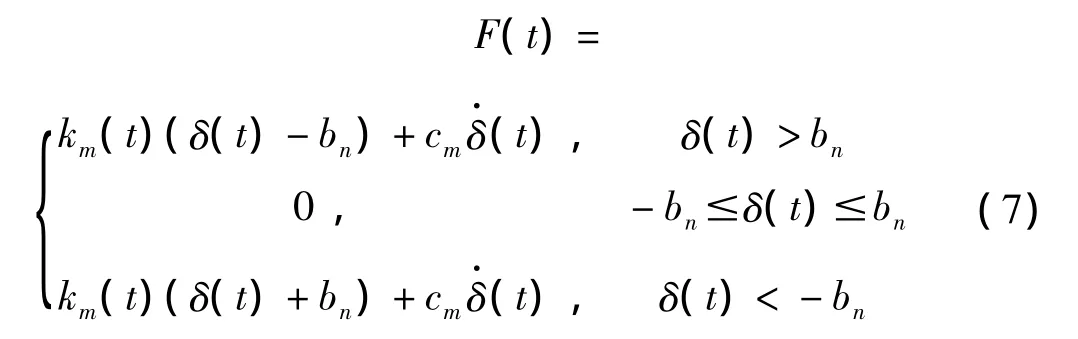
式中:cm是啮合阻尼。
此外,当沿y方向振动过大时,可能导致齿面、齿背同时接触,即产生所谓的挤齿现象,发生挤齿条件为:
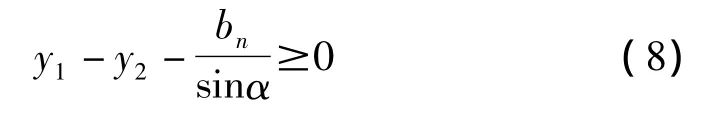
1.1.3 齿轮受力模型
对主动、从动轮进行受力分析,得到受力公式如下:
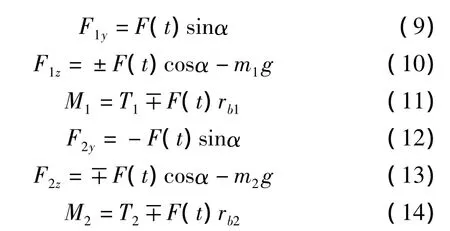
式中:F1y、F1z为主动轮在y,z方向受到的啮合力;F2y、F2z为从动轮在y,z方向受到的啮合力;M1、M2表示主、从动轮受到的力矩。rb1、rb2表示主、从动齿轮基圆半径;m1、m2表示两齿轮的质量;T1、T2是主、从动轮所受的转矩。
在正常啮合状态下,各公式取上面的符号;当发生齿背接触时,啮合力方向改变,各公式取下面的符号。
1.2 滚动轴承非线性接触力
图3(a)所示为球轴承,Dw为球径,D1为轴承外径,D2为内径,ur为轴承径向间隙。图3(b)为球轴承受力变形后球与套圈之间的位移-变形关系。假设外圈滚道沟曲率中心是固定的,内圈滚道沟曲率中心相对此中心而移动,滚动体质心也产生位移,内外圈接触角将不同。图中O1点为固定的外圈曲率中心,内圈沟曲率中心从O2点移动到了O'2点,球中心从Ob点移动到了O'b点。
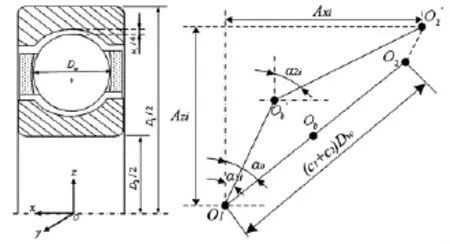
图3 滚动轴承几何关系Fig.3 Geometry relation of rolling bearing
图3中,c1、c2分别为外圈、内圈的沟曲率系数,α0为滚动体与套圈原始接触角,α1i、α2i分别为受载后第i个滚动体与外圈、内圈的接触角,Axi、Azi为内外圈沟曲率中心的轴向距离和径向距离,φi为第i个滚动体的方位角。由图中几何关系可求出滚动体与外圈、内圈的接触变形δ1i、δ2i,以及接触角,再由赫兹接触理论可得滚动体和套圈的接触力Q1i、Q2i。
考虑滚动轴承的离心力、陀螺力矩、惯性力、摩擦力,建立任意受载的滚动体拟动力学分析模型[20-21]。
内圈位移已知时,使用Newton-Raphson方法可求出各滚动体的接触力。可得滚动轴承的非线性接触力和力矩为:

式中:f1i、f2i为滚动体的摩擦力。rr2为内圈滚道沟曲率中心圆半径。
1.3 弹性转轴模型
使用有限元理论将弹性轴划分为若干个轴段,每个轴段单元采用两节点Euler梁单元模型,每个节点考虑6个自由度,包括横向弯曲振动(沿y、z轴)、轴向振动(沿x轴)、扭转振动(绕x轴)、扭摆振动(绕y、z轴)。如图4所示,两根弹性轴分别包括n1和n2个节点,i、j表示啮合齿轮在轴段上的节点位置。
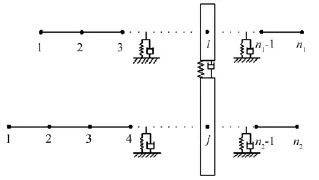
图4 齿轮轴承转子系统节点示意图Fig.4 Nodes of gear bearing rotor system
通过Euler梁单元模型,根据有限元理论,可得到轴段节点的质量、刚度、阻尼、陀螺和载荷矩阵。
1.4 整体法建模
采用整体法对齿轮、滚动轴承和弹性轴的质量、刚度、阻尼、陀螺和载荷矩阵进行组装。方法如下:
整体法是取各转子节点状态向量的集合X=[X1,X2,X3,…,Xn]作为系统的状态向量,Xi={xi,yi,zi,θxi,θyi,θzi},每个节点考虑 6 个自由度。组装维数为6(n1+n2)×6(n1+n2)的质量、刚度、阻尼、陀螺和载荷矩阵。其中,由于齿轮啮合力考虑3个自由度、轴承力考虑5个自由度,通过对应自由度补零的方法使其添加为6自由度矩阵。
整体法建模组装各矩阵的流程如图5所示。首先,输入初始条件,以齿轮副在转轴上的节点号ni和nj为基准,将两根轴的节点号排列为2行的矩阵;然后从转轴最左端节点开始组装,将节点的参数矩阵添加到相应的整体矩阵中,若一根转轴在另一转轴的对应节点处不存在节点,则将其在整体矩阵中对应的节点设为零矩阵;如该节点处有轴承支承,将滚动轴承质量、阻尼、轴承力矩阵组装到对应的节点上;对于齿轮耦合节点,考虑到齿轮间的耦合作用,在对应的节点位置上添加齿轮的质量矩阵、啮合力矩阵;直至所有节点全部组装,得到齿轮轴承转子系统的质量矩阵、阻尼矩阵、陀螺矩阵、刚度矩阵、载荷矩阵。
得到各矩阵后,可建立齿轮轴承转子系统的动力学模型如下:
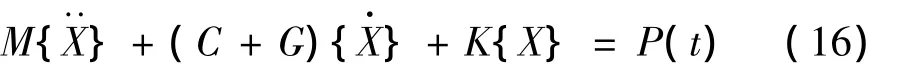
式中:质量矩阵M由转轴、轴承、齿轮质量组装得到;阻尼矩阵C由转轴、轴承阻尼组装得到;陀螺矩阵G、刚度矩阵K仅包含转轴项;载荷矩阵P(t)由外力、齿轮啮合力、非线性轴承力和重力组装得到。
2 计算方法
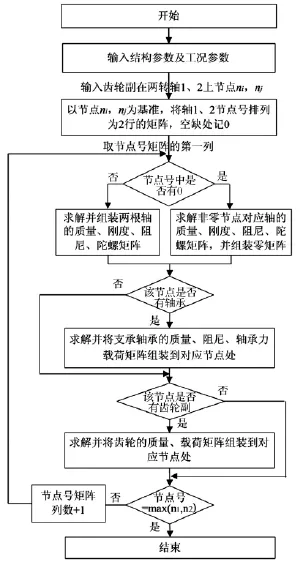
图5 整体法组装矩阵Fig.5 Matrix assemble using integration method
根据FPA修正法确定求解周期,采用Runge-Kutta法、Newton-Raphson法对非线性动力学方程组求解,通过时域图、频谱图、相图以及庞加莱截面图进行分析。然后求解最大Lyapunov指数,判断系统的动力学行为。
2.1 求解周期的确定
齿轮轴承转子系统中,存在齿轮啮合激励、轴承非线性变刚度激励,其中齿轮啮合力产生的激励其周期为轴转动周期的整数倍,但轴承的变刚度激励周期往往不是轴转动周期的整数倍,所以在判断和求解周期运动时,采用修正的FPA法建立统一的求解周期[22],定义求解周期如下:
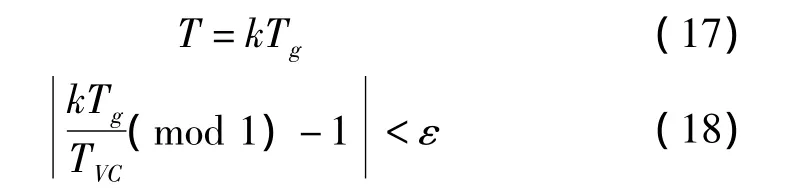
式中:T为求解周期,Tg为齿轮啮合激励周期,TVC为轴承变刚度激励周期,ε为常数,取ε=0.01,k=1,2,3,…。
根据上式循环计算,直至找到满足式(18)的k值,代入式(17)即得求解周期。
2.2 Lyapunov 指数计算
利用Lyapunov指数来判定是否存在混沌响应是目前最有效的方法之一。Lyapunov指数表示在相平面中2条相邻轨线间的距离随时间的平均指数发散率,它明确地区分了确定性运动和混沌运动。采用Wolf算法计算最大Lyapunov指数[23-24],对于连续系统:
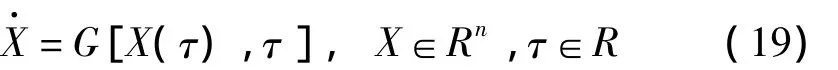
设(τ)为一基准轨线,X(τ)为其相邻轨线。定义向量X=(x1,x2,…,xn)T的范数为:
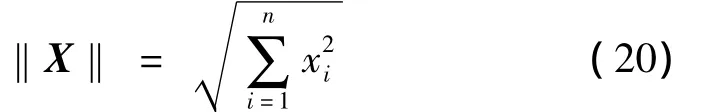
考察X(τ)与(τ)之间的距离随时间延续的发散程度。记:

设在τ0时刻‖δX(τ0)‖充分小,于是1维的Lyapunov指数定义为:
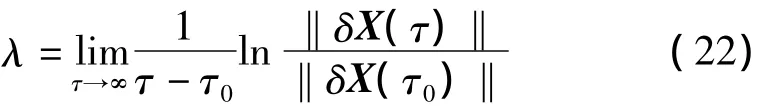
在n维连续系统中,δX(τ)在每个基底上有分量,每一个分量均可求出一个λ,因此共存在n个Lyapunov指数λi,称为 Lyapunov指数谱。当任意选取向量δX(τ)时,Lyapunov指数以概率1可能取得最大值,如果其中最大的Lyapunov指数λmax>0,则一定存在混沌运动。因此,只要计算出系统的最大Lyapunov指数,就可以判断系统是否处于混沌状态。
3 结果分析
对某齿轮轴承转子系统进行数值计算,两齿轮轴长度各400 mm,弹性模量为2×1011Pa,泊松比0.3,各由两个7306球轴承支承,轴承受预紧载荷200 N,齿轮传递扭矩100 N·m。主动、被动齿轮和支承轴承的结构参数如表1、表2所示。
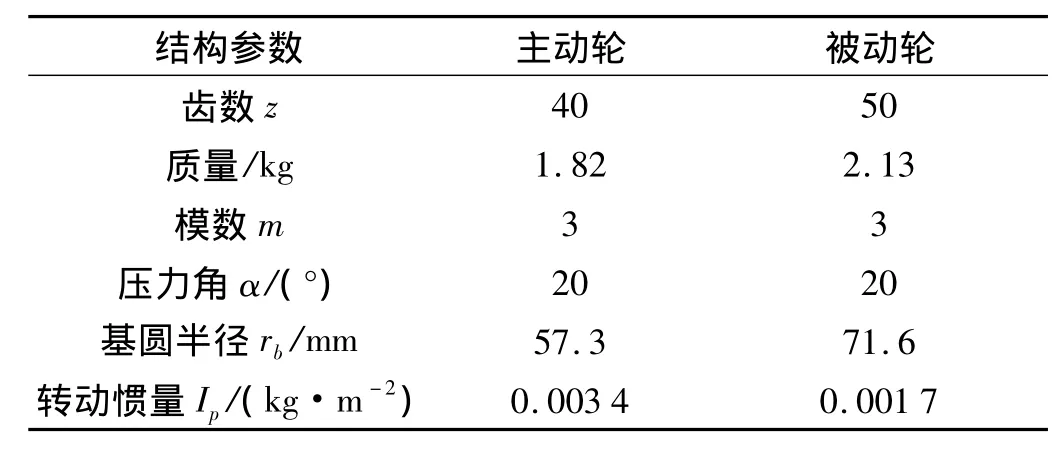
表1 齿轮结构参数Tab.1 Structure parameters of gears

表2 滚动轴承结构参数Tab.2 Structure parameters of rolling bearings
将两根齿轮轴各划分为5个节点,分析转速、齿侧间隙、转轴刚度、轴承径向间隙对系统非线性响应的影响,本文取从动轮节点处的弯曲振动响应分析。
3.1 齿侧间隙的影响
齿侧间隙会导致整个系统在运行过程中出现挤齿、脱齿、齿背接触等现象,造成齿轮单边冲击或双边冲击。其他参数不变的情况下,分析齿侧间隙对整个齿轮转子轴承系统的动力学特性的影响。
不同齿侧间隙时最大Lyapunov指数随转速变化如图6所示。可以看出,齿侧间隙为10 μm时,在2 900~3150r/min,最大Lyapunov指数大于零,系统出现混沌行为;当齿侧间隙为20 μm时,系统在2 750~3 300 r/min、4 300~5 400 r/min,系统出现了混沌行为,而当齿侧间隙为40 μm时,系统在2 700~ 3 350 r/min、4 150~5 500 r/min,出现混沌行为。随着齿侧间隙的不断增大,混沌区间逐渐变大。
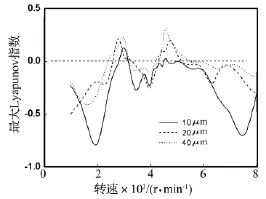
图6 不同齿侧间隙时最大Lyapunov指数随转速变化Fig.6 Variation of Maximal Lyapunov exponent with speed at different backlash
计算齿侧间隙为20 μm时z方向的振幅,如图7所示。在2 700 r/min处,振幅出现了跳跃现象。在转子转速为4 750 r/min时,出现了共振峰值。这是由于转速接近齿轮转子系统一阶弯扭耦合振动临界转速引起共振。
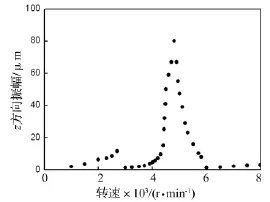
图7 齿侧间隙20 μm时的振幅Fig.7 Amplitude corresponding to 20 μm backlash
齿侧间隙为10 μm、转速为4 400 r/min,沿啮合线方向相对位移、沿y方向的相对位移、频谱图和Poincaré映射图如图8所示。可以看出,图8(a)所示沿着啮合线的相对位移大于齿侧间隙一半,说明齿轮正常啮合。图8(b)表示的啮合产生的y方向的相对位移小于零,根据式(8)中挤齿条件判断,系统未产生挤齿现象。图8(c)中频谱中仅有轴承变刚度振动频率fb、齿轮啮合频率fg,结合图8(d)Poincaré映射图为表明系统为周期运动。
齿侧间隙为20 μm、4 400 r/min时,相对位移、频谱图和Poincaré映射图如图9所示。图9(a)表明沿着啮合线的相对位移既存在大于齿侧间隙一半又存在小于齿侧间隙一半的现象,说明系统处于正常啮合与瞬时脱齿之间,即系统呈现单边冲击状态。图b)表明啮合产生y方向的相对位移偶尔会出现大于零的现象,表明系统出现轻微的挤齿。图9(c)频谱出现连续谱线,结合图9(d)Poincaré映射可知系统呈现混沌运动。

图8 转速4 400 r/min、间隙10 μm的响应Fig.8 Responses at 4 400 r/min and backlash of 10 μm

图9 转速4 400 r/min、间隙20 μm的响应Fig.9 Responses at 4 400 r/min and backlash of 20 μm
齿侧间隙分别为 10 μm、20 μm,系统一阶弯扭耦合临界转速附近4 750 r/min的Poincaré映射图如图10所示。图10(a)表明齿侧间隙为10 μm时系统为拟周期振动,图10(b)表明齿侧间隙为20 μm时系统为混沌运动。说明当齿侧间隙增大时,系统在一阶弯扭耦合临界转速附近由拟周期运动进入混沌运动。
以上分析可知,齿轮轴承转子系统中齿侧间隙对非线性动力学行为有重要的影响,随着齿侧间隙增大,齿轮系统会出现脱齿和挤齿现象,进入混沌运动且出现冲击。
3.2 转轴刚度的影响
齿侧间隙取20 μm,对转轴刚度的影响进行分析。在其他参数不变的情况下,分别取转轴长度为300 mm、400 mm、500 mm,转轴径向刚度分别为 2.61 ×107N/m、1.14×107N/m、0.59 ×107N/m,分析对齿轮转子轴承系统的动力学特性的影响。不同转轴刚度时对应的最大Lyapunov指数随转速的变化如图11所示。
转轴长度为300 mm时,在2 600~3 700 r/min、4 150~5 900 r/min,出现混沌行为。转轴长度为400 mm 时,在2 750~3 300 r/min、4 300 ~5 400 r/min,出现混沌行为。转轴长度为500 mm时,系统在2 800~3 200 r/min,出现混沌行为。可见,随着转轴长度增加即转轴刚度降低,系统混沌区间减小;共振转速附近产生混沌运动对应的转速降低,这是由于转轴刚度降低导致弯扭耦合振动临界转速减小,因此混沌运动的区间也发生改变。
转速为4 400 r/min、转轴长度为300 mm的响应如图12所示。图12(a)表明脱齿现象严重,系统出现单边冲击。图12(b)表明,有间歇性的挤齿现象。图12(c)证明系统为混沌运动。
转速4 400 r/min、转轴长度为500 mm的响应如图13所示,由图13(a)可知,无脱齿。图13(b)表明,无挤齿。13(c)证明系统为2周期运动。
对比图9、图12与图13可知,随着转轴刚度降低,系统由混沌运动逐渐转变为2周期运动;由严重脱齿逐渐减轻并变为不脱齿,由间歇性挤齿、轻微挤齿变为无挤齿;冲击现象也逐渐减轻并消失。
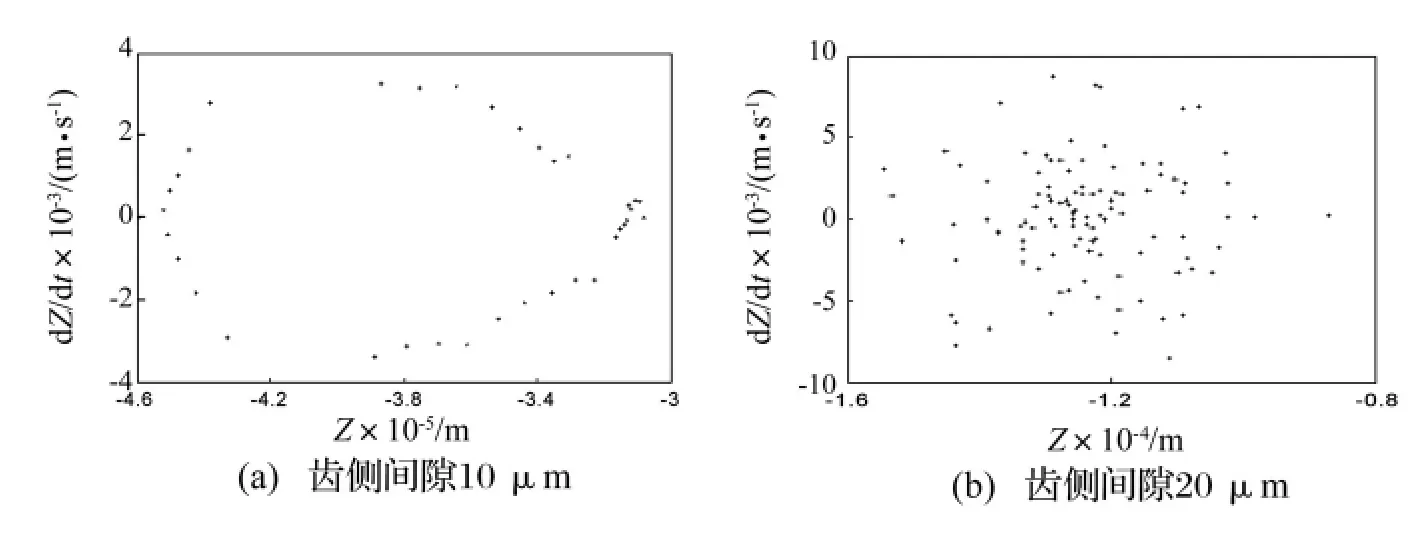
图10 不同齿侧间隙的Poincaré映射Fig.10 Poincaré figuresat different backlash

图11 不同转轴刚度时最大Lyapunov指数Fig.11 Maximal Lyapunov exponent at different stiffness
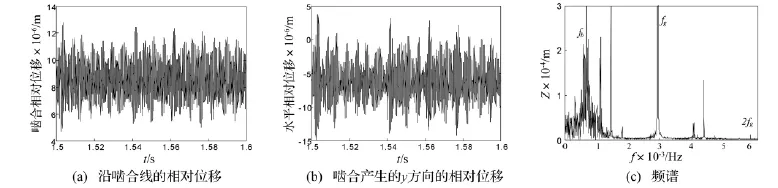
图12 转速4 400 r/min、转轴长度300 mm响应Fig.12 Responses at 4 400 r/min and shaft length is 300 mm
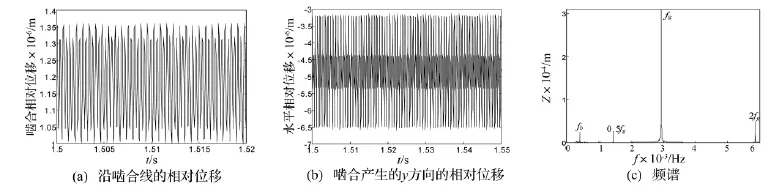
图13 转速4 400 r/min、转轴长度500 mm响应Fig.13 Responses at 4 400 r/min and shaft length is 500 mm
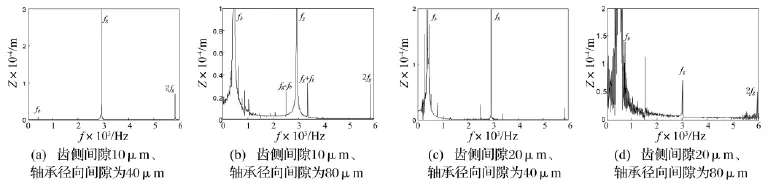
图14 不同间隙时的频谱Fig.14 Frequency spectrμm at different backlash and clearance
3.3 轴承径向间隙的影响
轴承径向间隙会导致轴承系统出现非线性行为。之前的研究因为轴承的振动幅值与齿轮相比较小而往往忽略,但随着结构参数与工况参数改变支承轴承的振幅可能很大[13-14],本文考虑轴承齿轮转子系统耦合影响,研究轴承的非线性对齿轮的影响。
图14(a)、(b)给出了转速4 400 r/min,齿侧间隙为10 μm、轴承径向间隙分别为40 μm、80 μm 时的频谱图,与图8(c)轴承径向间隙为60 μm时得到的频谱图对比,发现径向间隙为40 μm、60 μm时系统均为周期振动,但间隙为60 μm时轴承激励的幅值比间隙为40 μm时大;间隙为80 μm时发现啮合频率两侧出现轴承振动幅值调制产生的边频带,轴承振动频率附近出现了连续谱线,轴承变刚度激励的幅值增大,轴承非线性振动对系统的影响增大,系统由周期运动变为非周期运动。
图14(c)、(d)给出了转速4 400 r/min,齿侧间隙20 μm、轴承径向间隙分别为 40 μm、80 μm 时的频谱图。与图9(c)轴承径向间隙为60 μm得到的频谱图对比,发现三种参数下系统均为混沌运动,但随着径向间隙的增大,轴承激励的幅值明显增大,轴承振动对系统的影响增大,系统的混沌运动行为也变得更加明显。
4 结论
(1)齿侧间隙增大,系统混沌运动的转速区间变大,振幅出现跳跃现象;齿轮系统会出现脱齿和挤齿现象,由周期运动逐渐进入混沌运动且出现冲击;临界转速附近由拟周期运动进入混沌运动。
(2)随着转轴刚度降低,系统混沌运动的转速区间减少,柔性转轴对减少系统混沌运动有利;弯扭耦合振动临界转速减小;使系统脱齿、挤齿和冲击现象逐渐减轻。
(3)随着轴承径向间隙增大,轴承的非线性振动对系统的影响逐渐增大,轴承变刚度激励的幅值增大。
[1]王建军,李其汉,李润方.齿轮系统非线性振动研究进展[J].力学进展.2005,35(1):37-51.
WANG Jian-jun, LIQi-han, LIRun-fang. Research advances for nonlinear vibration of gear transmission systems[J].Advances in Mechanics,2005,35(1):37-51.
[2]Kahraman A,Singh R.Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system[J].Journal of Sound and Vibration,1991,146(1):135-156.
[3]王立华,李润方,林腾蛟,等.齿轮系统时变刚度和间隙非线性振动特性研究[J].中国机械工程,2003,14(13):1143-1146.
WANG Li-hua,LI Run-fang,LIN Teng-jiao,et al.Research on nonlinear vibration characteristics due to time-varying mesh stiffness and gear backlash in gear system[J].China Mechanical Engineering,2003,14(13):1143-1146.
[4]张锁怀,沈允文,丘大谋.齿轮耦合的转子轴承系统的不平衡响应[J].机械工程学报,2002,38(6):51-55.
ZHANG Suo-huai, SHEN Yun-wen, QIU Da-mou. On response of mass unbalance in a geared rotor bearing system[J].Chinese Journal of Mechanical Engineering,2002,38(6):51-55.
[5]Kubur M,Kahramang,Zini D M,et a1.Dynamic analysis of a multi-shaft helical gear transmission by finite elements:model and experiment[J].Journal of Vibration and Acoustics,2004,126:398-406.
[6] Maliha R,Dogruer C U,Ozguven H N.Nonlinear dynamic modelingofgear-shaft-disk-bearing systems using finite elements and describing functiom[J].Joumal of Mechanical Design,2004,126:534-541.
[7] Cai W,Chang J.Strong nonlinearity analysis for gear-bearing system under nonlinear suspension bifurcation and chaos[J].Nonlinear Analysis:Real World Applications,2010,11:1760-1774.
[8]Cai W,Chang J.Nonlinear analysis for gear pair system supported by long journal bearings under nonlinear suspension[J].Mechanism and Machine Theory,2010,45:569-583.
[9] Byrtus M,Zeman V.On modeling and vibration of gear drives influenced by nonlinear couplings[J].Mechanism and Machine Theory,2011,46:375-397.
[10]崔亚辉,刘占生,叶建槐.间隙非线性齿轮-转子系统的不平衡响应研究[J].振动与冲击,2008,27(S):29-31.
CUI Ya-hui,LIU Zhan-sheng,YE Jian-huai.Research on unbalance response of gear rotor system consider backlash[J].Journal of Vibration and Shock,2008,27(S):29-31.
[11]崔亚辉,刘占生,叶建槐.齿轮-转子耦合系统的动态响应及齿侧间隙对振幅跳跃特性的影响[J].机械工程学报,2009,45(7):7-15.
CUI Ya-hui, LIU Zhan-sheng, YE Jian-huai. Dynamic response of geared rotor system and the effect of clearance on jump characteristics of amplitude[J].Chinese Journal of Mechanical Engineering,2009,45(7):7-15.
[12]陈思雨,唐进元,谢耀东.齿轮传动系统的非线性冲击动力学行为分析[J].振动与冲击,2009,28(4):70-75.
CHEN Si-yu,TANG Jin-yuan,XIE Yao-dong.Analysis of nonlinear impact dynamic behavior for a gear pair system with time-varying stiffness and friction[J].Journal of Vibration and Shock,2009,28(4):70-75.
[13]李 明,孙 涛,胡海岩.齿轮传动转子-轴承系统动力学的研究进展[J].振动工程学报,2002,15(3):249-256.
LI Ming,SUN Tao,HU Hai-yan.Review on dynamics of geared rotor-bearingsystems[J]. JournalofVibration Engineering,2002,15(3):249-256.
[14]蒋庆磊,吴大转,谭善光,等.齿轮传动多转子耦合系统振动特性研究[J].振动工程学报,2010,23(3):254-259.
JIANG Qing-lei,WU Da-zhuan,TAN Shan-guang,et al.Development and application of a model for coupling geared rotors system[J].Journal of Vibration Engineering,2010,23(3):254-259.
[15]窦 唯,张 楠,刘占生.高速齿轮转子系统弯扭耦合振动研究[J].振动工程学报,2011,24(4):385-393.
DOU Wei,ZHANG Nan,LIU Zhan-sheng.The coupled bending and torsional vibrations of the high-speed geared rotor bearing system[J].Journal of Vibration Engineering,2011,24(4):385-393.
[16]Gupta T C,Gupta K,Sehgal D K.Instability and chaos of a flexible rotor ball bearing system:an investigation on the influence of rotating imbalance and bearing clearance[J].Journal of Engineering for Gas Turbines and Power,2011,133:1-11.
[17]张伟刚,高尚晗,龙新华,等.机床主轴-滚动轴承系统非线性动力学分析[J].振动与冲击,2008,27(9):72-75.ZHANG Wei-gang,GAO Shang-han,LONG Xin-hua,et al.Nonlinear analysis for a machine-tool spindle system supported with ball bearing[J].Journal of Vibration and Shock,2008,27(9):72-75.
[18]Cai Y.Simulation on the rotational vibration of helical gear in consideration of the tooth separation phenomenon[J].Journal of Mechanical Design,1995,117:460-468.
[19]李润方,王建军.齿轮系统动力学[M].北京:科学出版社,1997.
[20]Wang L Q,Cui L,Zheng D Z.Study on dynamic property of ball bearing system with nonlinear vibration of rotor[J].Journal of Mechanical Engineering Science,2008,222(C9):1811-1819.
[21]Harris T A.Rolling bearing analysis(4th Edition)[M].New York:John Wiley&Sons,Inc,2001.
[22] Choi S K,Noah S T.Response and stability analysis of piecewise linear oscillations under multi-forcing frequencies[J].Nonlinear Dynamics,1992,3:105-121.
[23] Wolf A,Swift J B,Swinney H L.Determining lyapunov exponents from a time series[J].Physica D,1985,16:285-317.
[24] Sundararajan P,Noah S T.An algorithm for response and stability of large order non-linear systems application to rotor systems[J]. JournalofSound and Vibration, 1998,214(4):695-723.
