低周往复荷载下空心矩形墩抗震性能试验研究
2013-02-13李建中
罗 征,李建中
(同济大学 土木工程防灾国家重点实验室,上海 200092)
近年来,随着中国高速公路的迅猛发展,大跨径高墩桥梁的应用也越来越多,为确保高墩的延性能力大于桥梁结构需求,满足公路桥梁抗震设计规范的要求,通常将高墩设计为空心薄壁构件,以减轻桥墩重量,增强构件延性。国内规范对此类桥墩的抗震设计缺乏明确的规定,空心墩的设计常常依据矩形墩的设计条文,不但造成材料的浪费,而且带来一定的安全隐患。为了改变这一现状,必须进行大量的试验研究,以掌握钢筋混凝土空心矩形薄壁墩的抗震性能和破坏机理。
同济大学宋晓东[1]以壁厚、配筋率为研究参数,长安大学崔海琴等[2]及北京工业大学杜修力等[3]以轴压比、配箍率为研究参数对矩形薄壁墩柱进行了拟静力试验,结果表明试件延性,耗能等抗震性能随着配箍率的提高、轴压比的降低而提高。本文将在前人研究的基础上,以配箍率、剪跨比为研究参数对矩形薄壁墩的抗震性能做进一步的试验研究。
1 试验设计

图1 截面钢筋布置(单位:mm)Fig.1 Configurations reinforce section(units:mm)
本次试验共有五个试件,编号分别为 405、805、902、905、908,其截面几何尺寸完全一致,外廓截面尺寸为768 mm×600 mm,壁厚100 mm。混凝土为C40,纵筋及箍筋均为Ⅱ级钢筋,。空心桥墩截面试件的尺寸如图—1、配筋如图—2所示。5个试件分成2系列,分别研究剪跨比、配箍率的影响。系列Ⅰ主要考察分析不同剪跨比的影响;系列Ⅱ则考察不同配箍率的影响。各试件的设计参数见表1,材料实测强度见表2。
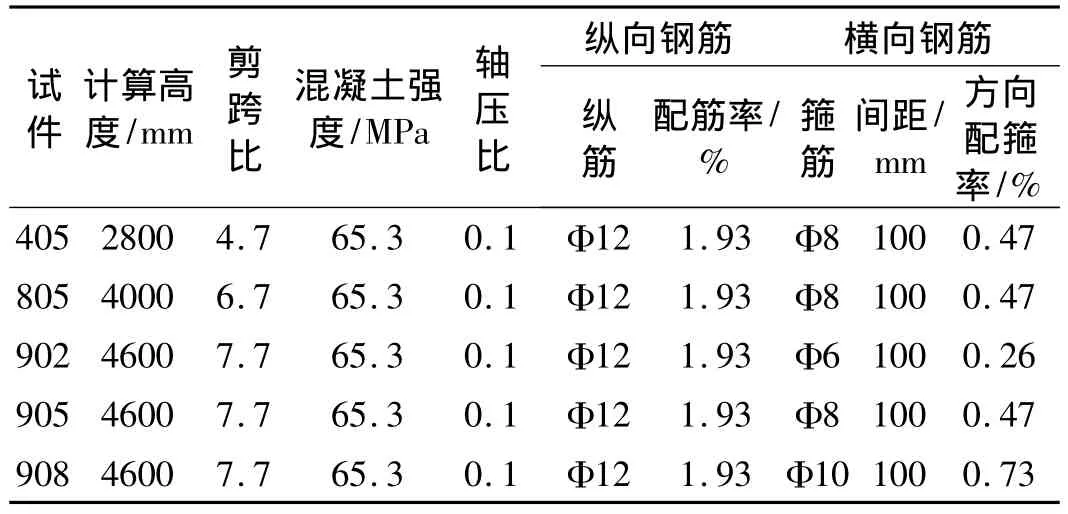
表1 构件参数Tab.1 parameters of specimens

表2 钢筋的材料参数Tab.2 Properties for the reinforcing steel
2 测试方案
2.1 加载装置
试验在同济大学土木工程防灾国家重点实验室进行,加载系统分为三个部分:竖向加载装置、水平加载装置、数据采集系统。竖向加载系统采用两个穿心式千斤顶贯穿两根高强螺纹筋,并张拉螺纹筋予以施加轴压力,千斤顶的作用方向会随着墩顶位移的变化而变化,轴力将始终平行于墩柱的轴线。水平荷载由德国SHENK公司生产的电液伺服高性能作动器来控制,作动器最大出力为600 kN;行程为 ±250 mm;加载示意图如图2。

图2 试验装置Fig.2 Experimental setup
2.2 测量仪器布置
试验过程中钢筋应变、试件各关键位置位移分别通过预埋应变片、设置位移传感器加以记录。其中,应变片主要预埋于墩底塑性铰区域的纵筋及箍筋上;位移传感器主要用于测量墩柱最大位移,塑性铰区域截面曲率。试验数据采用国产DH3817数据自动采集系统进行采集,采集频率最高可达8 Hz。
墩柱曲率测量采用回弹式位移计共计8个,安装在塑性铰区域的外伸横向钢筋上,用于测量墩底塑性铰区域的曲率,如图3所示。由塑性铰区域位移计测量出的竖向位移求得截面曲率,工作原理如图4所示。公式1为墩柱发生弯曲变形时,两侧混凝土纤维分别产生拉压变形h1、h2,D为截面宽度,则此时距墩底为H的截面曲率为:
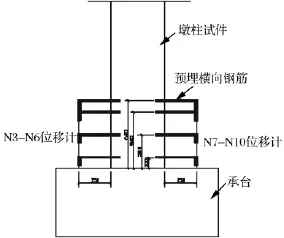
图3 塑性铰区域位移计布置立面图Fig.3 Elevation view of displacement gauges in the plastic hinge zone
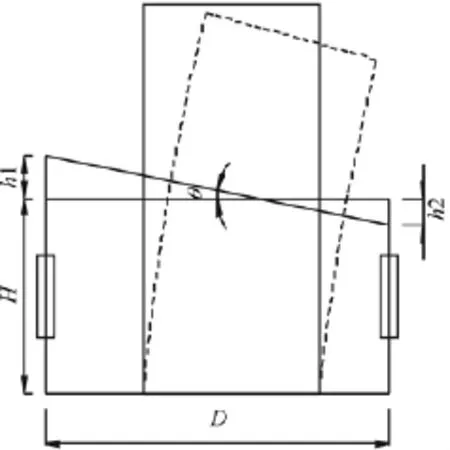
图4 曲率计算原理图Fig.4 Calculation principle of curvature
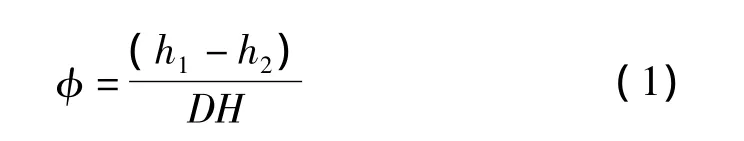
2.3 加载制度
首先沿轴心在试件顶部施加竖向荷载,墩柱轴压比为0.1;然后利用水平作动器对试件顶部施加低周往复水平荷载。在加载过程中采用位移和力混合控制的加载方式;其中位移控制阶段为等幅、变幅交错控制的加载过程。加载伊始采用力控制,每个试件对应进行3个力控制目标的加载过程,分别为开裂荷载控制、二级荷载控制、屈服荷载控制,每级力控制目标进行3个循环。在完成力控制加载过程后,加载方式转为位移控制,每个位移水平同样对应3个循环,直至试件破坏。
3 试验结果与分析
3.1 破坏过程及特征
总体说来,五个试件均为弯曲破坏,试件的各个破坏状态基本相同,破坏状态按照如下顺序发展:① 混凝土开裂② 钢筋屈服③ 混凝土保护层开始剥落④ 混凝土保护的完全剥落⑤ 纵筋的屈曲断裂。以试件805为例,简述其在各个加载阶段的破坏过程及破坏形态。荷载控制阶段,混凝土开裂之前,试件处于弹性工作阶段,其加载与卸载曲线基本重合且为一条直线。当水平推力为95 kN时,墩顶水平位移为20 mm,受拉的东、西两侧(垂至于加载方向)距墩底250 mm处受拉区出现了细微的水平开裂。随后观察到已有纵筋屈服,改为位移加载控制。加载位移为38 mm时,加载过程中沿着墩高向上出现新的裂纹,旧裂纹的长度和宽度也得到发展,位移等级达到50 mm时,试件正面裂纹继续增加及间距加密,在距墩底1 000 mm的高度内,裂纹都有出现。位移等级到达58 mm,角点处的混凝土保护层出现明显开裂。位移等级达到62 mm,角点处混凝土保护层开始剥落见图5。位移等级达到115 mm时,角点处明显混凝土剥落,剥落高度50 mm,宽度190 mm。位移等级达到130 mm时,角点处混凝土剥落区域加大,剥落高度60 mm,宽度200 mm。位移等级到达145 mm,角点处混凝土保护层完全剥落,露出纵筋,同时角点露出的纵筋屈曲。此时墩顶水平力达到的峰值荷载强度188 kN,。位移等级达到160 mm时,混凝土剥落区域继续增大,角点屈曲的纵筋断裂,但墩柱的荷载强度没有下降,墩顶水平力依然为188 kN。位移达到175 mm时,加载过程中,清楚的听到多根纵筋断裂的声音。同时,墩顶水平力开始下降为182 kN,相对峰值荷载强度能力下降3%,没达到试件破坏时承载力下降15%的要求,但出于保护加载仪器的需要,试验停止。由墩柱试件加载完毕图6可见,墩柱试件的正面距墩底150 mm的混凝土保护层完全剥落。
其余各个试件的破坏过程与上述情况基本相似,试件905位移等级达到157mm的时候,施加竖向荷载的其中一根高强螺纹钢筋的底座螺母脱落,导致螺纹筋拔出,其后改为无轴力加载。观察各个试件的破坏状态,可以得到如下结论:

图5 角点混凝土剥落(位移等级=62 mm)Fig.5 Spalling corer of concrete(displacement level=62 mm)

图6 试件最终破坏(位移等级=175mm)Fig.6 Final damage state(displacement level=175mm)
(1)当空心矩形墩角点区域混凝土完全剥落露出箍筋时,墩柱荷载强度达到最大,继续加载后,荷载强度降低或者保持不变。
(2)当空心矩形墩达到最终破坏状态,纵筋屈曲断裂后,箍筋未见断裂,核心混凝土保持良好。
(3)对于空心矩形墩柱,墩柱角点区域为空心矩形墩的易损区域,混凝土保护层的剥落及钢筋的屈服、断裂往往都是首先发生在墩柱角点位置。
3.2 滞回特性
以试件902为例对空心墩试件的位移滞回曲线进行描述见图7、曲率滞回曲线见图8。由位移滞回曲线可见,试件开裂前,加载和卸载曲线基本重合,滞回曲线近似为直线,试件处于弹性阶段,滞回环包围的面积极小。试件开裂后,滞回环面积逐渐增大,呈现梭形。试件屈服后,加载循环一次,循环加载对应的滞回环明显比首次加载的要窄、细。随后,滞回环越来越饱满。达到峰值荷载后,滞回曲线逐渐出现“捏缩”现象,这是由于裂缝的宽度增大,产生了滑移。与位移滞回曲线不同的是,曲率初始滞回曲线几乎与纵轴平行,使得屈服曲率取值较小,在其后的曲率延性的确定中,曲率延性能力值比位移延性能力值大的多。
3.3 延性及耗能指标分析
采用国外应用较为广泛的延性和耗能指标[4]对空心矩形薄壁墩延性抗震能力进行对比分析,耗能指标定义详见图11所示,图中Lf为墩柱破坏后混凝土剥落区域高度;t为截面宽度;m为累积加载次数。将计算得到的试件屈服位移 Δy、屈服曲率Φy、极限位移 Δu、极限曲率Φu、位移延性系数μΔ、曲率延性系数μΦ、极限侧移率R(R=Δu/L,L为墩柱计算高度)、工作损伤指标W和能量损伤指标E分别列于表3中。
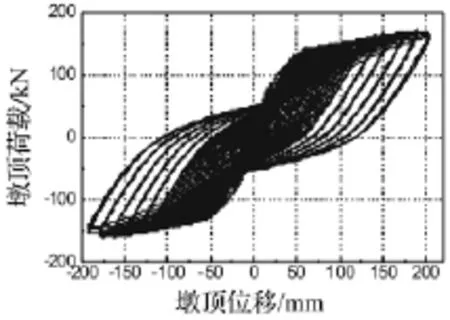
图7 墩柱滞回曲线Fig.7 Force-displacement response of bridge columns
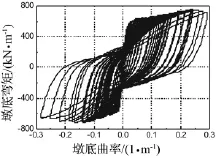
图8 墩底截面曲率滞回曲线Fig.8 Moment-Curvature response of pier bottom section
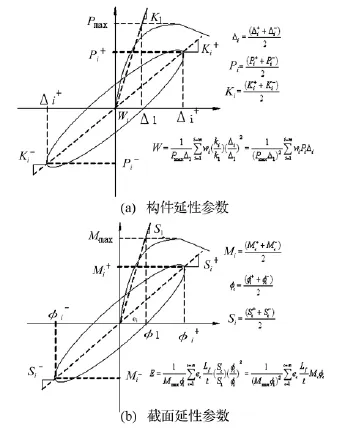
图9 延性参数定义Fig.9 Definitions of ductility parameter
位移延性系数μΔ、R及μΦ反映的是构件及截面的变形能力,工作性能指标W和能量损伤指标E体现的是试件与截面刚度退化与能量耗散综合能力。试件屈服位移采用国内外规范中普遍采用的等效屈服位移,其根据等能量法确定,具体做法见流程图11。由于空心墩试件破坏时承载力未下降至最大值的85%,本文以空心墩试件承载力达到最大值时的状态作为其的最终状态,试件905由于后期轴力缺失,未达到极限状态,数据未在图表中绘制。
目前,水生态保护修复的应用基础薄弱、关键技术缺乏,科技支撑能力不足,需加大投入,重点开展水工程生态学效应的基础理论研究,重要栖息地保护与修复、珍稀特有鱼类人工繁育与增殖放流、过鱼设施、生态流量保障与生态调度等关键技术的科技攻关,为长江大保护提供强有力的科技支撑。
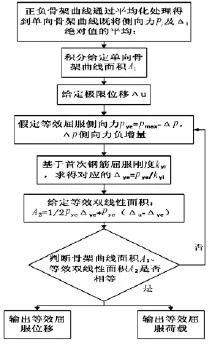
图10 等效屈服位移计算流程图Fig.10 The calculation flow chart of idealized yield displacement

表3 延性指标的对比Tab.3 Comparison of the ductility parameters
采用图10所示的方法将延性系数进行正负平均化处理按照剪跨比、配箍率的不同,绘制于对比图11~18中。
3.3.1 剪跨比的影响
剪跨比对墩柱抗震性能影响显著,构件405、805、905 剪跨比分别为 4.6、6.7、7.7,如图 11 所示,构件极限承载力随着剪跨比的减小而提高,试件405极限承载力比805提高了34%,同时在位移延性为4.4时,试件405、805出现了荷载下降段,试件405承载能力下降了2.4%,而试件805承载能力下降3.2%,说明剪跨比越大,荷载能力下降越快,且越早达到荷载下降15%的指标,空心墩柱剪跨比的位移延性随着剪跨比的增大而减小。能量损伤指标随墩顶位移延性的变化如图13。可以发现:墩柱未进入屈服阶段时即位移延性小于1时,空心矩形墩试件的能量损伤指标基本为零。墩柱进入屈服阶段以后时,空心矩形墩试件的能量损伤指随着位移延性近似呈现幂函数变化关系。国内学者孙治国[5]在文献中指出钢筋混凝土墩柱能量损伤指标在墩柱最终破坏状态下,剪跨比越大,能量损伤指标越小。图13为剪跨比不同的空心矩形墩试件能量损伤指标曲线,图中看出墩柱进入屈服阶段后,剪跨比越小,在相同的位移延性下的能量损伤指标越大,该结论与文献结论相同。
图12、14分别为截面层面的弯矩-曲率延性曲线及工作损伤指标-曲率延性曲线,图12所示,试件405相对于试件805极限弯矩强度提高了5%,同时曲率延性能力基本相等,说明剪跨比的提高对墩底截面极限弯矩强度影响不大,对截面曲率延性能力没有影响。图14所示,剪跨比越小,在相同的曲率延性下的工作损伤指标越大,与构件层面结论相同。
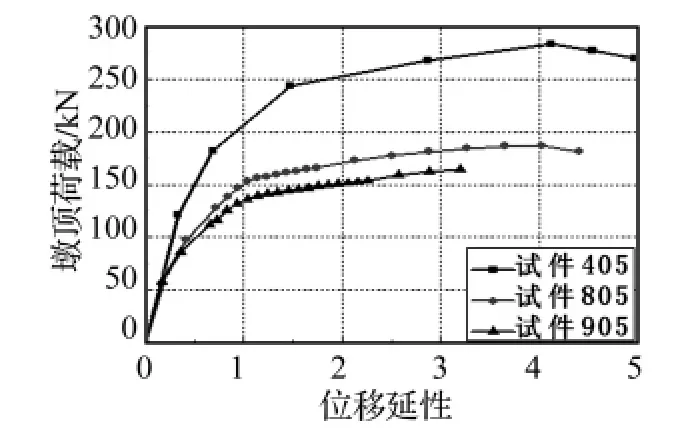
图11 405、805和905位移骨架曲线Fig.11 Force-displacement curves of 405、805、905
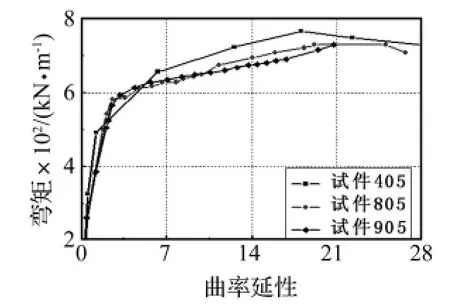
图12 405、805和905曲率骨架曲线Fig.12 Moment-curvature curves of 405、805、905
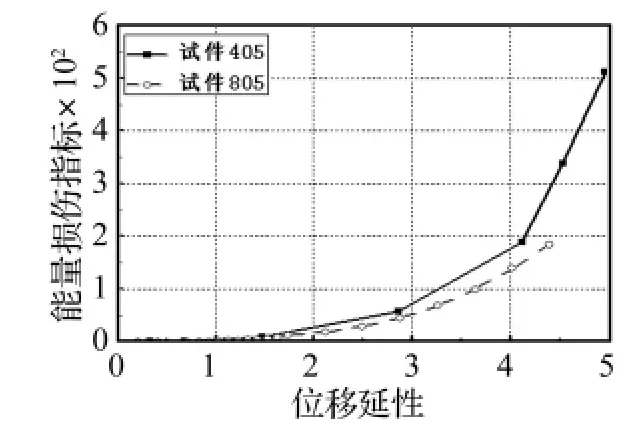
图13 405、805能量损伤指标Fig.13 Energy damage indicator of 405、805
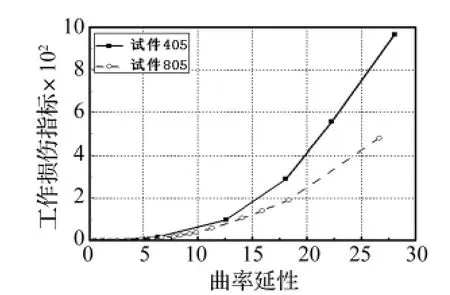
图14 405、805工作损伤指标Fig.14 Work damage indicator of 405、805

图15 902、905和908位移骨架曲线Fig.15 Force-displacement curves of 902、905、908
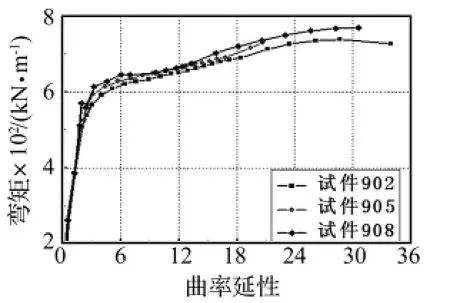
图16 902、905和908曲率骨架曲线Fig.16 Moment-curvature curves of 902、905、908
3.3.2 配箍率的影响
试件 902、905、908的配箍率不同,分别为 0.62、1.11、1.73,试件 908 比 902 的极限承载力仅提高了4%,同时如图15所示,在位移延性为3.9时,试件902承载能力下降1.8%,而试件908承载能力没有下降,说明配箍率越小,荷载能力下降越快,越快达到荷载下降15%的指标,故空心墩柱的位移延性随着配箍率的增大而增大。图17为配箍率不同的空心矩形墩试件能量损伤指标曲线,由图看出墩柱在延性小于2时,配箍率不同的曲线基本重合;延性大于2后,在相同的位移延性下,配箍率越大,能量损失指标越大,说明配箍率的提高会提高墩柱能量损伤指标。
图16、18分别为不同配箍率的截面层面弯矩—曲率延性曲线及工作损伤指标—曲率延性曲线,由图可以得到与构件层面相同的结论,即配箍率的提高对试件极限承载力影响甚微,但曲率延性及耗能能力显著提高。
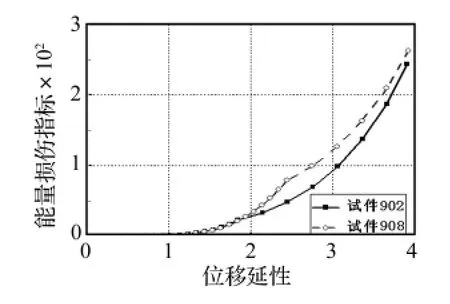
图17 902、908能量损伤指标Fig.17 Energy damage indicator of 902、908

图18 902、908工作损伤指标Fig.18 Work damage indicator of 902、908
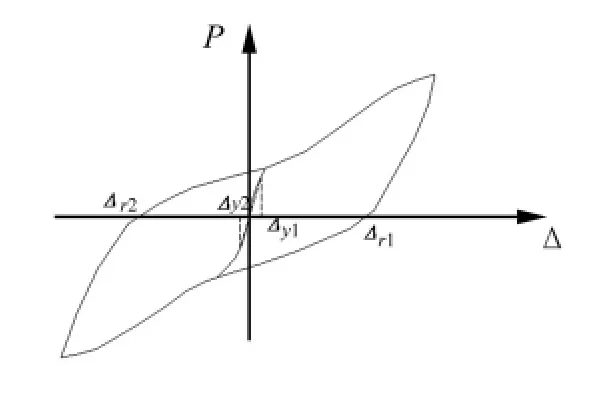
图19 残余位移示意图Fig.19 Schematic diagram of residual displacement
3.4 残余位移延性指标
桥梁墩柱的残余位移是震后桥梁是否能继续服役的重要指标。日本神户兵库县在神户地震后,研究者发现尽管有的桥梁墩柱残余位移侧移率超过1.5%,墩顶位移超过150 mm,但是桥梁结构并没有倒塌。说明墩柱在震后允许有残余位移,但是残余位移过大,将引起构件修复的困难,以及诸多不安全因素,所以,残余位移的研究有着重要的实际意义。
本文采用Hose[6]所提出的残余位移指标RDI对残余位移进行研究,残余位移指标RDI的定义如图19。
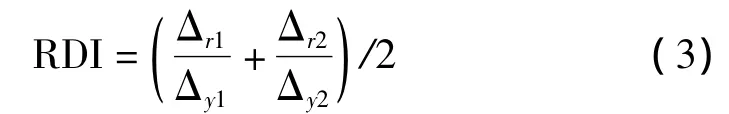
式中:Δr1正加载方向残余位移(mm);Δr2负加载方向残余位移(mm);Δy1正加载方向等效屈服位移(mm);Δy2负方向等效屈服位移(mm)。
日本抗震设计规范[7]中规定在第二级地震性能水准下,地震后桥墩处产生的残余位移Δr须满足下列条件:
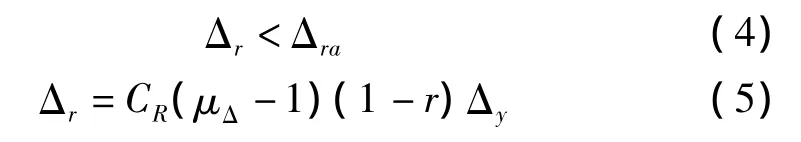
式中:Δra为墩柱允许残余位移,取值为1/100的墩柱高度,即墩柱允许残余位移侧移率比为1%。Δy为墩柱屈服位移;CR为残余位移系数,规范建议取值0.60;μr为为桥墩反应延性系数;r为桥墩屈服刚度与屈后刚度之比定义的双线性系数,规范建议取值0;
将上式的残余位移按照残余位移指标表达,同时代入规范建议值,则上式变为:

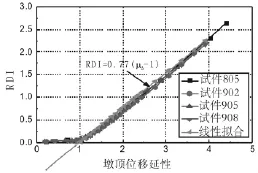
图20 空心墩试件残余位移指标Fig.20 Residual displacement index of hollow piers
5个空性墩柱残余位移指标如图20所示,在位移延性小于1时,延性残余位移指标基本为零。位移延性大于1时,残余位移指标随着位移延性的增加线性递增。试件405的由于加载级数过少,同时残余位移左右位移偏差较大,未在图中体现。不同剪跨比与配箍率的4个试件残余位移指标曲线基本重合,说明剪跨比与配箍率两参数的变化对残余位移指标无影响。对试验数据进行线性拟合得到残余位移指标与位移延性的关系式:与公式6进行比较发现,日本规范中的残余位移公式符合实际情况,但系数CR取值偏小,本文建议取值CR=0.77。

4 结论
(1)本次试验中的钢筋混凝土空心桥墩,在低周往复荷载和竖向轴压的共同作用下,均发生弯曲破坏,抗震性能好,同时空心试件最终破坏时,纵筋屈曲断裂,但核心混凝土保持良好。
(2)配筋率相同,剪跨比的减小使钢筋混凝土空心桥墩的承载力、位移延性和耗能能力都有提高,但对墩底截面极限弯矩、曲率延性没有影响。
(3)配箍率对空心墩的极限承载力与墩底极限弯矩影响不大,却大大提高了位移延性、曲率延性和耗能能力。
(4)根据日本规范中对于残余位移计算模型提出的修正计算公式更加符合工程实际应用。
[1]宋晓东.桥梁高墩延性抗震性能的理论和试验研究[D].上海:同济大学,2002.
[2]崔海琴,贺拴海,宋一凡.空心矩形薄壁墩抗震性能试验研究[J].公路交通科技,2009,27(6):58-63.
CUI Hai-qing,HE Shuan-hai,SONG Yi-fan.Test study on seismic performance of hollow rectangular thin-walled pier[J].Highway Jiaotong Technology,2009,27(6):58-63.
[3]杜修力,陈明琦,韩 强.钢筋混凝土空心桥墩抗震性能试验研究[J].振动与冲击,2011,30(11):254-259.
DU Xiu-li, CHEN Ming-qi, HAN Giang. Experimental evaluation of seismic performance of reinforced concrete hollow bridge columns[J].Journal of Vibration And Shock,2011,30(11):254-259.
[4]Bayrak O,Sheikh S A.Confinement reinforcement design considerations for ductile HSC columns[J].Journal of Structural Engineering,ASCE,1998,124(9):999-1010.
[5]孙治国,司炳君,王东升,等.高强箍筋高强混凝土柱抗震性能研究[J].工程力学,2010,27(5):128-136.
SUN Zhi-guo, SI Bing-jun, WANG Dong-sheng, et al.Research on the seismic performance of high-strength concrete columns with high-strength stirrup [J]. Engineering Mechanics,2010,27(5):128-136.
[6]Hose D,Frieder Seible.Performance evaluation database for concrete bridge components and systems under simulated seismic loads[R].Pacific Earthquake Engineering Research Center,PEER Report 1999/11.
[7]Japan Road Association,Design specification of highway bridge,part[S]:Seismic Design,2002.
[8] Sheikh S A,Shah D V,Khoury S S,Confinement of highstrength concrete columns[J].ACI Structural Journal,1991,91(1):100-111.
[9]Lehman D E,Moehle J P.Seismic performance of wellconfined concrete column[R].PEER Report 1998/01.
[10] Brachmann L,Browning J,Matamoros A.Drift-dependent confinement requirements for reinforced concrete columns under cyclic loading[J].ACI Structural Journal,2004,101(5):669-677.
