基于灰色理论的数控机床主轴热误差温度测点优化*

赵昌龙

(长春大学机械与车辆工程学院，长春 130022)

基于灰色理论的数控机床主轴热误差温度测点优化*

赵昌龙

(长春大学机械与车辆工程学院，长春 130022)

为了保证数控机床的加工精度，提高其加工质量，针对影响数控机床热误差的机床主轴温度场分布问题，对主轴系统在加工过程中的温度场变化情况进行了实际的测温实验，在实验的基础上利用灰色理论中关联度分析的方法，对主轴温度场上温度传感器的优化布点进行了研究，从初始实验中的8个温度测点减少到3个关键的温度测点，更有利于提高今后的建模及热误差预测的精度。

灰色系统;热误差;数控机床;测点优化

0 引言

随着人们对现代制造技术要求的不断提高，数控机床正向高精度、高效率以及高自动化方向发展，如何控制数控机床在工作过程中所产生的热误差控制问题也已成为提高机械加工精度的一个关键问题。由于机床各部件温升引起的热变形，使机床上刀具与工件之间原来相对正确的位置发生了改变，从而造成了加工误差。整个主轴系统作为数控机床最为重要组成部件之一，是引起热误差变形的最重要的因素［1-5］。我们从设计和制造技术的角度出发改进主轴结构可减小热误差，但其成本较高，采用热误差补偿技术来减小热误差从而提高机床加工精度则是一种更为有效、更为经济的途径。

在对机床进行热误差补偿之前，首先要对主轴温度场的分布进行测量并建模，一般说来，布置在主轴上的温度测点数目越多，所建立的热误差模型也就越精确，对热误差的估计也越准确，但是布置过多的温度传感器会大大增加数据处理的工作量，同时，出于对系统成本的考虑有必要对温度测点的布局进行优化和处理，以较少的测点代替多测点争取表明温度场变化，从而简化热误差补偿系统［6-7］。但是运用传统的数理统计方法，例如回归分析等方法对于处理主轴热误差这种包含了复杂因素的非线性系统比较困难，而利用灰色理论可以在小样本的情况下，对内部没有明显规律的系统进行分析，而且计算量很小且方法简单，能够获得系统中存在的某些未知的内在规律，并对整个系统以后可能出现的发展状况进行预测，最后实现系统的优化与组合。

本文实际测量了机床主轴温度场的分布情况，并利用灰色系统的基本理论，根据实际测得的温度场统计数据序列，建立起灰色关联分析模型，并分析机床主轴系统温度场中各个测点对其热误差影响的重要程度，并对其进行综合性能评价并进行相对优劣排序，从整个温度场温度测点中选出影响程度最关键的点，从而达到减少测点数量的目的，避免了由于温度变量过多造成的布线过多等诸多问题［8-11］。

1 主轴温度场及热误差的检测

1.1 主轴测温硬件系统

本文使用的机床主轴测温系统由8个型号为DS18B20的智能型温度传感器、一块芯片为89C51的开发板、串口线以及电脑组成，测温系统组成及工作流程图如图1所示。智能温度传感器将获得的主轴温度数据通过开发板和RS232接口实时传送到电脑中，在电脑中通过温度采集软件系统可以实时显示并对数据进行储存，以便后期的数据处理。

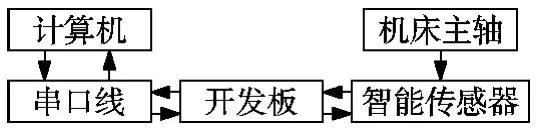
图1 系统组成及工作流程图

1.2 主轴测温软件系统

主轴测温软件控制系统流程图如图2所示。在运行测量程序之前，可以确定采样通道，设定采样时间，然后开始采集数据，程序可以将采集来的数据实时显示在界面中，并可以将各个采样点数据储存在硬盘中。

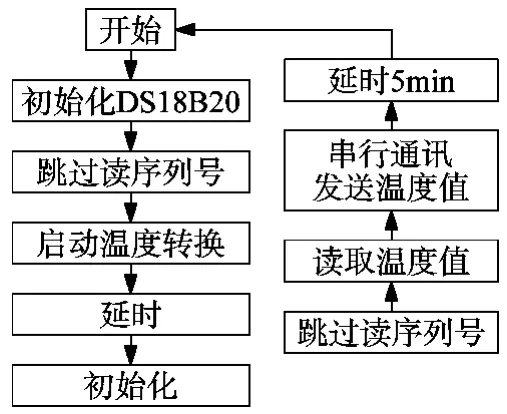
图2 温度采集软件系统流程图

1.3 主轴温度布点

在实际布点的过程中，考虑到加工中心主轴的实际结构，若主轴实际长度为L，则将1号传感器放置在前轴承处，8号传感器放置在后轴承处，在前轴承和后轴承之间等距离安放6个传感器［12］。主轴温度布点实物图如图3所示。而主轴热误差则通过固定在工作台上的位移传感器进行测量，主要测量主轴Z方向上的热误差。

图3 主轴温度布点实物图

1.4 加工中温度场及热误差测量实验

测量试验中模拟机床加工过程，为了分析方便，实验中忽略了切削对热误差造成的影响，主轴以8000r/min的转速进行空切削，采样周期为5min，同时对主轴温度场和主轴Z方向热误差进行测量。主轴温度场和热误差变化如图4a、b所示。

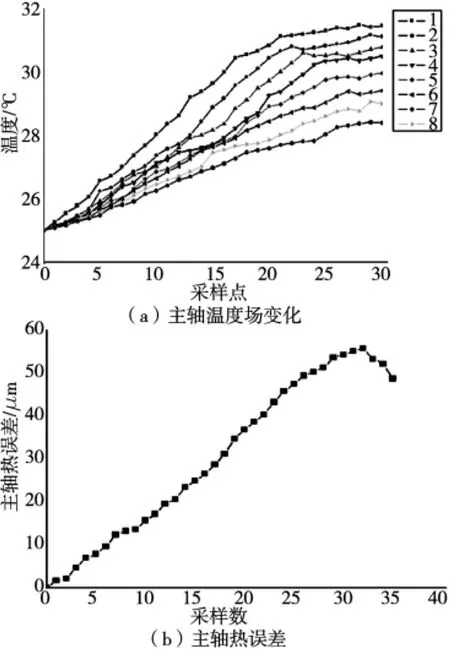
图4 数据采集曲线

2 灰关联度分析模型

灰色系统分析是依据整个系统中每个特征参量系列之间的近似程度用数学理论所进行的系统分析。在处理实验数据的过程中，灰色系统理论具有其他传统统计理论无法比拟的优点，即在实验样本较少并且所研究系统概率未知的情况下，计算结果可以充分体现所研究系统存在的内在规律［13］。本文在对机床主轴各测温点的测量数据进行分析时，通过灰色系统理论的灰色关联度分析法，找出系统中各因素间的相互关系，从而寻出影响主轴加工热误差的主要因素，以减少测温点数目，方便建立热误差预测模型。

2.1 数据序列的规范化处理与灰关联系数

设有参考数列x0={x0(k)|k=1，2，…，m}及比较数列xi={xi(k)|i=1，2，…，m}，在计算灰关联系数之前，首先要对所有数列进行规范化数据处理，这是为了便于今后的比较，并保证各因素间具有等效性和同序性，使其无量纲化和归一化。本文对原始数据采用了三种处理方法，分别是初值化变换、均值化变换和极差化变换。初值化变换是将所有数据均用第一个数据除，然后得到一个全新的数列，为数列中每个不同时刻的值相对于第一时刻的值的百分比。均值化变换法是用所有数据的平均值去除所有数据，得到的新数列为占平均值百分比为多少的数列，而极差化变换法有两种变换形式，本文采用其中一种，即数值越大效用越小的因素处理法，具体处理过程如下式:

q为分辨系数，q ∈［0，1］，一般取 q=0.5，在实际处理过程中，可根据各数据序列间的关联度，对q取值进行适当调整，以增加分析中的分辨能力。

2.2 灰关联度

两个序列间的关联度可以利用其各个时刻关联度系数的平均值来表示，如式3

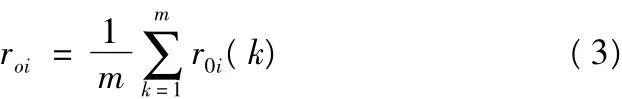
式中，r0i为子序列i与母序列的关联度;m为两个比较序列的数据个数。

最后按照所得各个子序列对同一母序列的关联度按大小将子序列顺序排列起来，继而组成了关联序，它能够直观的反映出各个子序列对同一母序列影响程度的大小关系，所得数值越大则表示这一子序列对母序列有着相对大的影响程度。

3 主轴温度场灰关联模型的应用分析

在主轴温度场测点的优化过程中，引入了灰关联度分析模型，此模型可以分析出多个因素对主行为的影响程度的大小，即找出影响主轴热误差的诸多温度测点中最为重要的测点位置，以最少的测点个数反应整个温度场的变化情况。考虑到在实际测量温度场的过程中所得数据比较多，同时灰关联模型对数据采集的等时距性，具体选取的时间节点以25分钟为一个采样周期，共选取了7个节点。以机床主轴径向热误差为母序列x0，安装在主轴上的8个温度传感器所测得的数据数列为子序列xi。

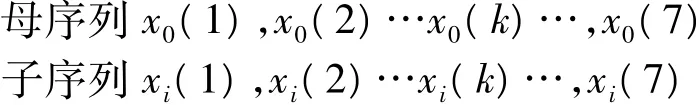
在将最初的实验数据进行规范化处理，消除了量纲影响的基础上，得到不同时刻子序列xi与母序列x0的关联系数和关联度。关联度计算结果如下:

(1)通过初值化变换法所得各时刻子序列与母序列的关联度:

运用初值化变换法、均值变换法以及极差化变换法进行处理后，本文得到了三个灰关联序，从中我们可以找到每一个关联序中关联度最大的因素分别为 r01、r04、r08，即主要影响因素为 r01、r04、r08。实验中与之对应的三个传感器分别为:

r01为1号传感器，位于主轴前轴承处;r04为4号传感器，位于距离主轴前轴承3/7L处;r08为8号传感器，位于主轴后轴承处。经过灰关联度模型分析出的对主轴热误差影响最大的三个主要因素，即三个传感器所测量的温度能够准确的反应出整个主轴温度场的变化情况。

4 结束语

本文在实际测温实验的基础上，运用灰色系统理论的关联分析方法，进行各因素对主行为的影响程度的分析和确定，即数控机床在加工运行过程中，确定各数控机床主轴温度场各个温度测点对其热误差的影响程度，将原来8个温度传感器减少到3个温度传感器，有效的确定了机床主轴热误差建模时所需的关键温度变量的最优组合，分别是测量主轴前轴承、后轴承和距离主轴前轴承3/7L处，而且计算过程十分简单、计算量很小，更有利于之后所进行的数控机床主轴系统热误差建模预测及补偿，提高其预测补偿精度。

［1］窦小龙，杨建国，等.温度测点优化在机床主轴热误差建模中的应用［J］.航空精密制造技术，2003，39(4):33－36.

［2］J.L.Deng，Control problems of grey system，Systems and Control letterΙ，1982(5):288－294.

［3］Y.P.Huang，CC.Huang，CH.Huang，Determination of the preferrred fuzzy variables and applications to the prediction control by the grey modeling，in:Proceeding of the Second National Conference on Fuzzy Theory and Application，1994.

［4］J.L.Deng，Introduction to grey system theory.The Journal of Grey System Ι，1989(1):1－24.

［5］F.M.Tseng，G.H.Tzenge，The comparison of four kinds of predicitionmethods:ARIMA，fuzzy time series，fuzzy regression time series and grey forecasting-an example of the prediction value forecast of machinery industry in Taiwan，in:proceedings of the Second National Conference on Grey Theory and Applications，Taiwan，1997.

［6］S.He，Y.Li，R.Z.Wang，A new approach to performance analysis of ejector refrigeration system using grey system theory.Applied Thermal Engineering，2009(29):1592 －1597.

［7］Huang，J.T，Lin，J.L.，“Optimization of machining parameters setting of die-sinking EDM process based on the Grey relational analysis with L18 orthogonal array，”J.Techol.2002，17:659 －664.

［8］Fung，C.P.，Huang，C.H.，Dong，J.L，“The study on the optimization of injectionmolding process parameterswith Gray relational analysis，”J.Reinf.Plast.Comp，2003，22(1):51－66.

［9］Chorng-Jyh Tzeng，Yu-Hsin Lin，Yung-Kuang Yang，Ming-Chang Jeng，“Optimization of turning operationswithmultiple performance characteristics using the Taguchi method and Grey relational analysis，”Journal of Materials Processing Technology，2009，209(3):2753－2759.

［10］Yang Jianguo，Deng Weiguo，Ren Yongqiang，Li Yuansheng，DouXiaolong，“Grouping Optimization modeling by Selecting of Temperature Variables for the Thermal Error Compensation on Machine Tools，”China Mechanical Engineering，2004，15(3):478 －481.

［11］ Cao Yongjie，Fu Jian-zhong，“Study on Optimal Layout temperature measurement for thermal errors of spindle in machine tools，”Modular Machine Tool＆ Automatic Manufacturing Technique，2007(1):61－64.

［12］ Xiang Hongwei，Zheng Li，Liu Dacheng，Zhao Daquan，“Thermal Error Model for Spindle of Machine Tool，”Manufacturing Technology＆ Machine Tool，2000(11):12－14.

［13］Y.X.Li，J.G Yang，T.Gelvis，Y.Y.Li，“Optimization of measuring points for machine tool thermal error based on grey system theory，”Int J Adv Manuf Technol，2008，35(1):745－750.

［14］Wong K，“Extension relational algebra and grey relational algebra，”ACM SIGICE Bulletin，1997，22(4):17 －24.

［15］Wong K，“Grey functional dependency in numerical relational database，”In Proc ISCA International Conference，1995(6):203－207.

(编辑 赵蓉)

Optim ization of Measuring Points Based on the Grey System Theory for Spind le of CNC Machine Tool

ZHAO Chang-long
(College of Mechanical and Automotive Engineering;Changchun University，Changchun 130022，China)

To improve processing precision of numericalmachine tool，research on analyze the thermal error of spindle，the grey correlation analysismethod is used to optimize the thermal key points to build themodel of temperature field on the basis of temperaturemeasurement experiment.By optimizing，the number of temperaturemeasuring points from 8 to 3.In this way，the precision of thermal error model and thermal error prediction can be improved.

grey system;thermal error;CNC machine tool;measuring point optimize

TH161

A

1001－2265(2013)03－0021－03

2012－08－17

吉林省教育厅项目:吉教科合字［2011］第343号

赵昌龙(1979—)，男，吉林长春人，长春大学机械与车辆工程学院博士，讲师，主要研究方向是精密加工技术、数控装备与数字制造技术，(E－mial)zhao19790204@126.com。