空载试验台飞轮系统设计及其模态分析
2013-02-05林巨广江宏勇蔡高坡
林巨广,江宏勇,蔡高坡
(1.合肥工业大学 机械与汽车工程学院,合肥 230009;2.安徽巨一自动化装备有限公司,合肥 230051)
空载试验台飞轮系统设计及其模态分析
林巨广1,江宏勇1,蔡高坡2
(1.合肥工业大学 机械与汽车工程学院,合肥 230009;2.安徽巨一自动化装备有限公司,合肥 230051)
针对变速箱空载试验台的飞轮系统进行了结构设计,并基于ANSYSWorkbench有限元分析软件对其进行了模态分析。对于轴承座,地基和滚动轴承等并非是绝对刚性的情况,为了更好地模拟飞轮系统运行时的实际工况,对影响系统最大的轴承的支承刚度进行了计算,为系统添加了弹性约束。经过分析得出了飞轮系统的固有频率和临界转速,并通过尺寸修正,提高了低阶固有频率,改善了飞轮系统高速运转时的抗振性能。
飞轮系统;支承刚度;模态分析
0 引言
空载试验台主要用于检测变速箱在运行状态下的换挡性能。通过该试验台,可以及时发现变速箱的异响、振动、干涉、卡滞等现象。为了能够准确模拟汽车在行驶过程中产生的惯量,在设计空载试验台时添加了飞轮组件。
飞轮质量很大,会使转动轴产生一定的变形,特别在运转中有不平衡力存在的情况下这种变形将会增大。纵使这些变形很小,但是这对承受较大负载的转动轴来说,对其寿命影响却是很大。另外,如果轴的尺寸结构设计不当引起共振,很可能会造成试验台损坏的事故。因而,在设计时对飞轮组件进行振动模态分析显得尤为重要。
1 飞轮系统的结构设计
考虑变速箱实际运行的工况,根据文献[1]对试验台所需的模拟惯量进行计算,得出模拟惯量为14 kg·m2。据此设计了直径520mm,厚度135mm的两片形状尺寸相同的飞轮,并通过胀紧套将两片飞轮固定在转动轴上。飞轮组件及安装结构如图1所示。

图1 飞轮组件安装结构图
由图1可知飞轮组件主要由飞轮、胀紧套、转动轴、调心滚子轴承、锁紧螺母以及支座等零部件组成。其中飞轮通过胀紧套固定在转动轴上,而锁紧螺母对支撑转动轴的调心滚子轴承进行预紧定位。
相对于飞轮与飞轮轴热装过盈配合的安装方式,用胀紧套连接飞轮和转动轴可大大减小飞轮系统的制造成本和技术难度。同时在进行转动轴的结构设计时,中间部位采用了宽度为50mm,直径为120mm的轴肩结构。通过此结构,可以保证飞轮准确的安装在左右两支撑座的中间位置,避免因为不对称而使左右轴承受力不等,引起受力较大的轴承磨损加剧,缩短飞轮系统的使用寿命,同时此种结构可以有效加强转动轴中间部位强度,改善轴的变形情况,而又不会明显增加轴的重量。
2 模态分析的理论基础
由弹性力学有限元法,可得飞轮系统的运动微分方程为:

式中:[M]、[C]、[K]分别为飞轮系统的质量矩阵、阻尼矩阵和刚度矩阵;
{f(t)}为飞轮系统的外界载荷向量。
公式(1)是一组耦合方程组,需要将其解耦后得到非耦合方程组才能求解。对解耦后的非耦合方程组求解,使其变成多组相互独立的方程。在这些相互独立的方程中,每个方程都只含有一个独立的模态坐标,这些相互独立的方程就是模态方程。这个求解的过程就是模态分析要完成的任务。
在本例中,飞轮系统所受外界载荷可忽略不计,故{f(t)}=0。这时飞轮处于自由振动状态。又因在求解自由振动的固有频率和振型时阻尼的影响不大,因而阻尼可视为零。进一步得飞轮系统的运动微分方程为:
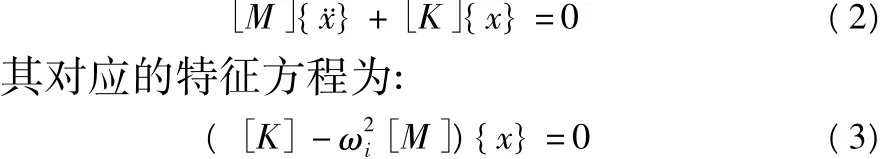
求解方程(3)可得各阶模态的固有频率ω1,ω2,…,ωi。再将各阶固有频率带入方程(3)可得对应的特征向量[xi],也即第i阶主振型。
3 基于Workbench的模态分析
3.1 飞轮系统有限元模型的建立
飞轮系统三维模型采用Pro/E软件构建,并导入Workbench分析软件进行有限元建模。飞轮系统中转动轴材料采用45号钢,飞轮材料采用铸铁,查相关手册得45号钢与铸铁的弹性模量、密度和泊松比,如表1所示。

表1 转动轴和飞轮的材料属性
连接飞轮的胀紧套由于结构比较复杂,不利于网格划分,故在不影响分析结果的情况下将其简化为外形尺寸相同的筒状零件,材料定义为45号钢。同时,为了方便网格划分,建模时去除转动轴上的倒角和螺纹等。划分网格时,采用自动网格划分,精度为中等,得到如图3所示的有限元模型。有限元模型节点数为49571个,单元数为27352个。

图2 转动轴的网格划分
3.2 约束条件的施加
在模态分析中,约束条件对分析结果有着很大的影响。如果约束施加不合理,可能得不到准确的分析结果。飞轮系统中,转动轴的两端分别用调心滚子轴承支撑于支撑座上,然后用锁紧螺母对滚动轴承进行预紧。由于轴承中油膜、游隙等诸多因素的存在,滚动轴承并非刚性体,所以转动轴所受的约束不是刚性约束而是弹性约束。同时由于受负载的变化和预紧力的不同,轴承的支承刚度也会不同。故在对飞轮系统施加约束之前必须对轴承刚度进行计算。
忽略转速对轴承刚度的影响,轴承的径向刚度的估算公式为[6]:
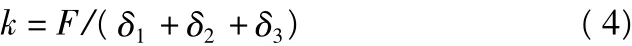
式中:F——轴承的径向负荷,N;
δ1——轴承的径向弹性位移,mm;
δ2——轴承外圈与支撑座的接触变形,mm;
δ3——轴承内圈与轴径的接触变形,mm。
已知飞轮系统中轴承所受载荷为F=2000N,轴承的预紧量g=-8μm,调心滚子轴承型号为22217E,查得轴承的相关参数并计算得:

对转动轴施加弹性约束,将调心滚子轴承简化为轴的弹性支撑,即可对轴进行模态分析。
3.3 模态分析
在实际工程应用中,低阶固有频率对应的临界转速往往可能处在工作转速内,很容易引起设备的共振。故在设计之初就有必要对零件进行分析,找出其固有频率和临界转速。这里对转动轴进行模态分析提取前3阶固有频率便已满足分析需要。
分析可得各阶固有频率和临界转速如表2所示。
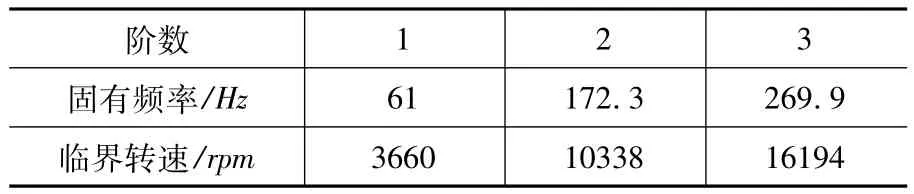
表2 系统的各阶固有频率和临界转速
试验台飞轮系统的最高设计转速为3000rpm,从表2可以看出系统的一阶临界转速明显高于这一转速。
在进行旋转件设计时,为避免共振和减小振动,应使其工作转速远离临界转速而处在一定范围之外。根据文献[5],当零件工作转速低于一阶临界转速时,工作转速应小于0.8nc1(nc1为一阶临界转速);当零件工作转速高于一阶临界转速时,工作转速应选在1.4nck<n<nck+1(nck、nck+1分别为第ck阶和ck+1阶临界转速)之间。由于飞轮系统的一阶临界转速3660rpm的0.8倍为小于最高设计转速,故为安全起见,有必要通过尺寸修正来提高系统的一阶临界转速,以使得工作转速处在一阶临界转速一定范围之外。
为此,提出更改和胀紧套配合处轴径尺寸的方案。为配合胀紧套的选型,将轴径依次更改为95mm,105mm。因轴径变化,相应的轴承型号也发生了变化。通过3.2节公式算出方案中轴承的支撑刚度如下:k1=117.74N/μm,k2=133.01N/μm。
对轴施加约束,通过Workbench软件分析可得不同轴径的飞轮系统的一阶固有频率和对应的临界转速如表3所示:
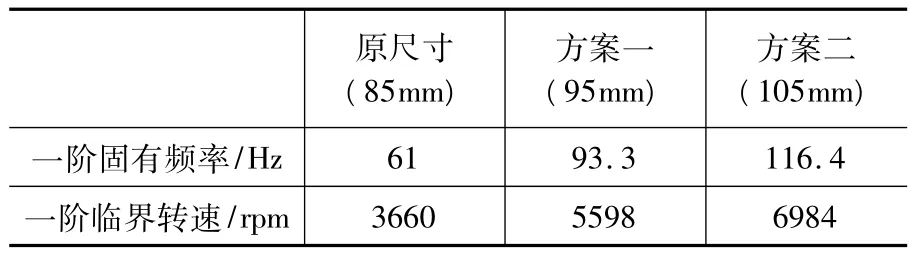
表3 不同方案对应的一阶固有频率和一阶临界转速
方案一和方案二的一阶临界转速0.8倍分别为4478.4rpm和5587.2rpm,均大于最高工作转速。由于轴的尺寸增大,轴的成本和技术要求也更高,所以虽然方案二将一阶临界转速提高许多,但是在满足临界转速和静强度的条件下还是选择方案一。
方案一的各阶固有频率和临界转速如表4所示,各阶振型图如图3所示。

表4 方案一的各阶固有频率和临界转速

图3 飞轮系统的各阶振型
4 结束语
(1)分析发现增大轴径尺寸,飞轮系统的固有频率增加。其原因有两个方面,一是轴径的增大使得轴截面积增大,进而提高了轴的刚度;二是轴径尺寸变化引起轴承型号的变化,由计算结果可知,轴承改变后,相应的轴承的支承刚度也增加了。
(2)方案二相对于方案一固有频率增加了很多,但是,由于增加轴径尺寸同时也会增加制造成本和难度,所以在满足静动态要求的情况下,选择方案一。
(3)虽然改变飞轮系统的支承跨距也可改变系统的固有频率,但是飞轮系统的结构已经非常紧凑,在有限的尺寸内无法达到要求,所以选择改变轴径的方案。
试验台经调试运行后,在高速工作时具有良好的运转状态,飞轮系统运行比较平稳,达到了设计的要求。
[1]谢峰,盛军,刘波,等.汽车变速器在线加载试验台可变加载装置的研究[J].组合机床与自动化加工技术,2007(7):46-49.
[2]张有禄.机械式汽车变速箱试验方法与应用[J].机械工程与自动化,2009(1):159-161.
[3]李兵,何正嘉,陈雪峰.ANSYSWorkbench设计、仿真与优化[M].北京:清华大学出版社,2008.
[4]巫少龙,张元祥.基于ANSYSWorkbench的高速电主轴动力学特性分析[J].组合机床与自动化加工技术,2010(9):20-26.
[5]徐龙祥.高速旋转机械轴系动力学设计[M].北京:国防工业出版社,1994.
[6]陈忠.滚动轴承及其支承的刚度计算[J].煤矿机械,2006,27(3)387 -388.
[7]戴曙.机床滚动轴承应用手册[M].北京:机械工业出版社,1993.
[8]夏田,马晓钢,张功学.基于 ANSYS Workbench的DVG850滑座的拓扑优化[J].机械设计与制造,2011(1):107-108.
(编辑 李秀敏)
Structure Design and Modal Analysis of Flywheel System on the No-load Test Bed
LIN Ju-guang1,JIANG Hong-yong1,CAIGao-po2
(1.School of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei 230009,China;2.JEE Automation Equipment Co.,Ltd.,Hefei230051,China)
The structure of the flywheel system on the no-load test bed of gearbox has been designed,and modal analysis is carried out on it by the finite element software ANSYSWorkbench.According to the situation that the bearing pedestal,subgrade and rolling bearing are not rigid,in order to well simulate actual conditions,a research ismade on the bearing stiffnesswhich has the largest impact on the system and finally the elastic support is successfully added to the system.Through the analysis,natural frequency and critical speed are obtained.Then by modifying the size,natural frequency is increased and the condition of vibration-proof ability of the flywheel system when it is in high speed is improved.
flywheel system;bearing stiffness;modal analysis
TH16;TG65
A
1001-2265(2013)03-0084-03
2012-09-10
林巨广(1963—),男,安徽六安人,合肥工业大学机械与汽车工程学院教授,博士生导师,主要从事汽车自动化装备的研究、汽车试验台等研究,(E -mail)jhyby118@163.com。
