K2n-1×K2n+1'的邻点可区别全染色①

张 琛， 王欣欣

(陇东学院数学与统计学院，甘肃 庆阳745000)

2004 年，在全染色的基础上，张忠辅，陈祥恩等［1］提出了图的邻点可区别全染色这一新概念，得到了一些有价值的成果，并根据这些结果提出了一个猜想:对于阶数不小于2 的简单连通图，其邻点可区别全色数不超过最大度加3.要完全证明这一结论较为困难，但目前已有的结果中，该猜想均成立.本文中所讨论的相邻奇数阶完全图的直积图的邻点可区别全色数也不超过这一上界.

1 定义及引理

本文所考虑的图均为连通、有限、无向的简单图.Δ(G)，d(v)分别表示图G 的最大度和图G 中顶点v 的度.其它术语及符号参［2］.

定义1 对图G(V(G)，E(G))，t 是正整数，S是t 元集，f 是从V(G)∪E(G)到S 的映射. 如果

1)对∀uv，vw ∈E(G)，u ≠w，有f(uv)≠f(vw)，

2)对∀uv ∈E(G)，有f(u)≠f(v)，f(u)≠f(uv)，f(uv)≠f(v)，

3)对∀uv ∈E(G)，有Cf(u)≠Cf(v)，这里Cf(u)= {f(u)}∪{f(uv)| uv ∈E(G)}叫做点u在f 下的颜色集合，且记¯Cf(u)= S -C(u)，则f 叫做图G 的t -邻点可区别全染色. 简称t -AVDTC.χat(G)= min{t| G 有t -AVDTC}叫做图G 的邻点可区别全色数.

定义2 对图G1= (V1，E1)和G2= (V2，E2)，直积图G1× G2的顶点集为V × V2，点(u1，v1)与(u2，v2)相邻当且仅当u1u2∈E1，v1= v2∈V2或者u1= u2∈V1，v1v2∈E2.

显然有G1× G2≌G2× G1，Δ(G1× G2)=Δ(G1)+ Δ(G2).

定义3 如果图G 的一个边子集M 中，每条边的两个端点不同，且任两边在G 中不相邻，则称M为图G 的一个匹配.

引理1［1］如果图G 有两个相邻的最大度点，则χat(G)≥Δ(G)+2.

引理2［1］Kn是n(n ≥3)阶完全图，则

其中χt(Kn)为Kn的全色数.

引理3［3］Kn是n(n ≥3)阶完全图，则

其中χas'(Kn)为Kn的邻强边色数.

本文给出了相邻奇数阶完全图的直积图K2n-1× K2n+1' 的邻点可区别全色数.

2 主要结果

定理1 对于相邻奇数阶完全图的直积图K2n-1× K2n+1'(n 为正整数)，则

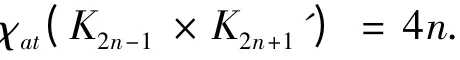
证明 在K2n-1× K2n+1'中，记vij= (ui，uj')，用K2n+1' 表示顶点集为V(K'(i)2n+1)= {vi1，vi2，…，vi，(2n+1)}的2n +1 阶完全图，用K2n-1表示顶点集为的2n - 1 阶完全图.

由定义2 知，K2n-1× K2n+1' 是两个边不交的子图与的并集.即

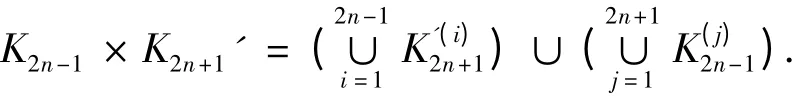
显然K2n-1× K2n+1' 为正则图，且χat(K2n-1×K2n+1')= 4n -2，由引理1，χat(K2n-1×K2n+1')≥4n.下仅需证明K2n-1× K2n+1'存在4n - AVDTC 即可.

可分三步定义一个从E(K2n-1× K2n+1')∪V(K2n-1× K2n+1')到色集{a0，a1，…，a2n，b0，b1，…，b2n-2}的映射f.

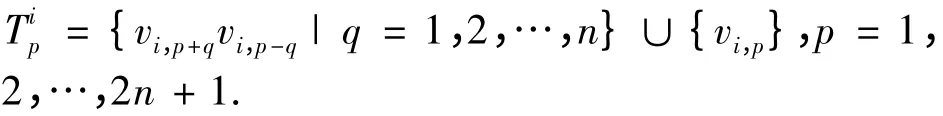
其中下标p + q 与p - q 取模2n +1.

显 然，Ti1，Ti2，…，Ti2n+1是 E(K2n+1') ∪V(K2n+1')的一个划分.对任意i = 1，2，…，2n -1，令

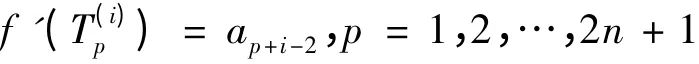
其中下标p + i -2 取模2n +1.

其次，用2n - 1 种色b0，b1，…，b2n-2染完全图的边，由引理3，使其成为的2n -1 - 邻强边染色，其中j = 1，2，…，2n + 1. 具体地，设的2n -1 个最大匹配为

其中下标t + s 与t - s 取模2n -1.

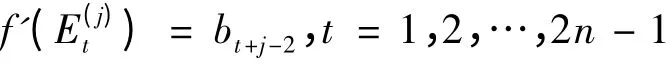
其中下标t + j -2 取模2n -1.

容易验证，f'为K2n-1×K2n+1'的4n -正常全染色，且有

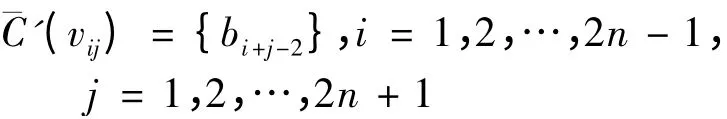
其中下标i + j -2 取模2n -1.

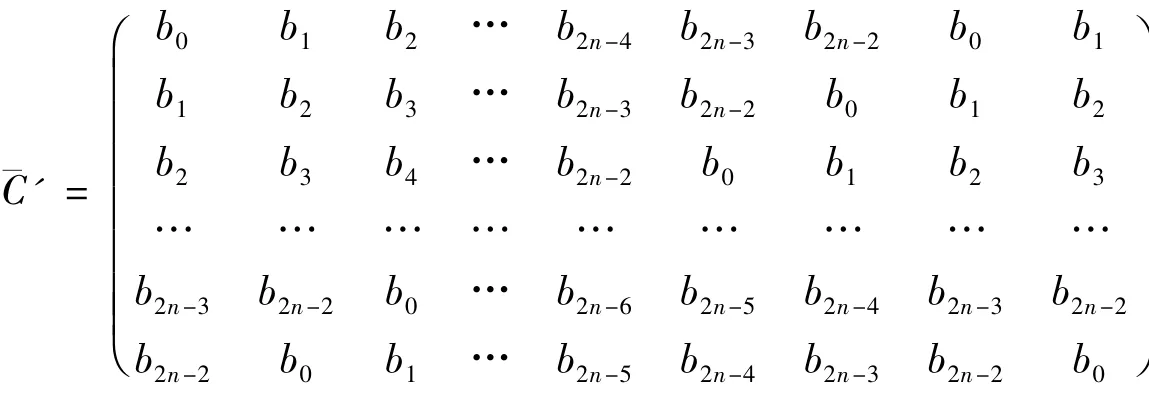
第三步，观察矩阵¯C'，每一列的任意两元素均不相同.而每一行的前2n - 1 个元素互不相同，但第1 列和第2n 列，第2 列和第2n +1 列元素完全相同，故下面对顶点vi，2n和vi，2n+1(i = 1，2，…，2n -1)进行改染.

其余顶点和边的染法不变，即令

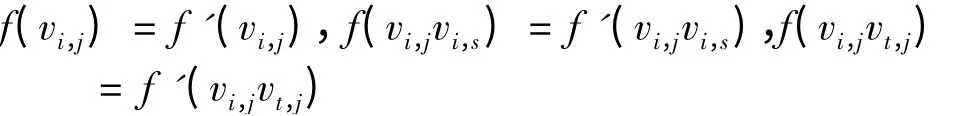
其中i ≠t，i，t = 1，2，…，2n -1;j ≠s，j，s = 1，2，…，2n -1.

下说明f 是K2n-1×K2n+1'的邻点可区别全染色.

若用矩阵¯C 表示在染法f 下各顶点色集的缺色情况，则有

因此，f 是K2n-1× K2n+1' 的4n - AVDTC.

对于任意奇数阶完全图的直积图K2s+1×K2t+1，若2s +1 与2t +1 不相邻，如使用上述定理1 中的染色方法，不能构成K2s+1×K2t+1的邻点可区别全染色.因此对于任意奇数阶完全图的直积图K2s+1×K2t+1的邻点可区别全染色还需要做进一步的讨论.

［1］ ZHANG Zhong-fu，CHEN Xiang -en，etc. On Adjacent -Vertex-Distinguishing Total Coloring of Graphs［J］.Science in China Ser.A Mathematics，2005，48(3):289 -299.

［2］ Bondy J. A. and Murty U.S.R［M］.Graph Theory with Applications，Macmillan［M］. New York:Longdon and Elsevier，1976.

［3］ ZHANG Zhong - fu. Adjacent Strong Edge Coloring of Graphs［J］.Applied Mathematices letters，15(2002):623 -626.

［4］ 张琛，张如清，吕卫东. K2s×K2t的邻点可区别全染色［J］.数学的实践与认识，2012，42(20):213 -216.

［5］ 陈祥恩，张琛.直积图的邻点可区别全染色［J］. 兰州理工大学学报，2008，34(2)，137 -140.

［6］ 张琛，陈祥恩，刘信生. 多重Mycielski 图的邻点可区别全染色［J］.西北师范大学学报，2007，43(6):22 -26.