对一道高三调研试题的探究

☉江苏省西亭高级中学 陆王华

对一道高三调研试题的探究

☉江苏省西亭高级中学 陆王华

前苏联数学家奥加涅相说：“必须重视，很多习题潜藏着进一步扩展其数学功能与教育功能的可行性.”某市2012-2013学年第一学期高三期末考试第18题（解析几何题）是一道涉及定点、定值的探究题，就是这样的好题.笔者通过对该题的拓展及探源，使这道测试题真正体现它的思维价值，同时也享受数学探究的方法与乐趣.

一、试题呈现

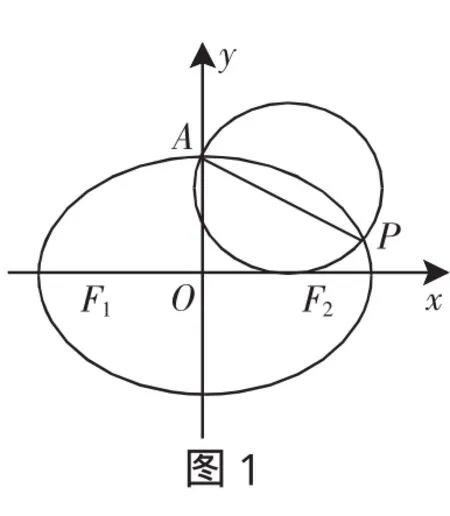
（1）求椭圆C的方程.

（2）若动直线l与椭圆C有且只有一个公共点，试问：在x轴上是否存在两定点，使其到直线l的距离之积为1？若存在，请求出两定点的坐标；若不存在，请说明理由.

首先看命题专家提供的答案.

综上，存在两个定点（-1，0）、（1，0），使其到直线l的距离之积为定值1.

上面的解法突出直线的斜截式，根据直线与椭圆相切，得到k与p的关系，过程自然，但运算量较大.如果设切点P（x0，y0），直接得到椭圆切线l的方程，一可避免对直线斜率是否存在的讨论，二可减少计算量.

所以存在两个定点（-1，0）、（1，0），使其到直线l的距离之积为定值1.

从上面的解法可以看出，根据椭圆上点P的坐标直接写出切线方程，要简捷得多！如果在学习中我们将该题解决后就完事大吉，放弃对该题的探究，自然领悟不到此题的价值，从而错失一个好的试题应有的功能.

二、该题的一般性结论

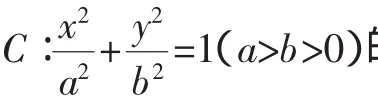
三、探寻试题的源头

弄清试题的源头，有助于把握问题的来龙去脉，促进我们把握知识之间的内在联系.该结论绝不会是凭空想出来的，它的得来一定与我们见过的一些基本结论或题型有联系.它的源头在哪里呢？

首先我们可以想象：当椭圆的两个焦点无限接近时，椭圆的形状越来越趋近于圆，因此圆可以看成焦点重合于圆心的椭圆.而圆心到圆上一点处的切线的距离显然为半径，但在椭圆中就无法确定是a2还是b2了.能否从椭圆的几何性质入手来探寻呢？

进一步思考：能否用平面几何知识加以证明：椭圆两个焦点到椭圆的切线的距离之积为定值b2呢？经过探究发现是可以的！为了能简捷证明这条性质，先解决一个与椭圆的切线有关的又一结论：

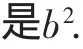
最后还需说明一下，既然椭圆与双曲线有这样的性质，那么对于抛物线y2＝2px（p＞0），虽然没有两个焦点，那么，在x轴或y轴上是否存在两点到抛物线上任一点P（x0，y0）处的切线y0y＝p（x+x0）的距离之积为定值呢？经过探究，答案是否定的，即在x轴或y轴上不存在这样的两点.限于篇幅，这里不予赘述.