单绕组无轴承开关磁阻电动机绕组电流计算

李 群，邓智泉，曹 鑫，冯绍兵

(南京航空航天大学，江苏南京210016)

0 引 言

基于磁轴承与电机相结合的思想，将无轴承技术应用于开关磁阻电动机(以下简称SRM)，形成了无轴承开关磁阻电动机(以下简称BSRM)。BSRM除了具有磁悬浮电机摩擦小、速度高、寿命长等优点之外，同时还具备普通SRM高容错性、高速适应性强和耐高温性能好等优点，因而在高速电机、航天航空和军民两用等领域有独特的应用优势。近些年来，SRM的无轴承技术逐渐成为研究的热门方向。

BSRM的研究最早始于日本学者，传统的BSRM是在普通BSRM的定子齿极上再增加一套绕组用于电机悬浮，通过对定子齿极上两套绕组的电流大小以及导通的宽度进行控制，使电机能够悬浮旋转［1－3］。但是，双绕组 BSRM 需要设计两套绕组，同时还存在着装配复杂等一系列问题［4］。因此单绕组BSRM的研究越来越受到关注。目前，对单绕组BSRM的研究主要集中在12/8、8/6齿极结构以及8/10等定转子变化结构上［5－17］。美国学者 B.B.Choi以及中国台湾的学者Yang S.M.对12/8极单绕组BSRM技术进行了研究［5－7］。其电机的各个定子齿极上无需额外增加绕组，本体结构与普通的SRM完全相同，通过对绕组电流的大小进行合理的控制，即能使电机运行在悬浮的状态。对8/6极单绕组BSRM技术进行研究的主要是学者Chen L.等人［8－10］。他们采用在一相导通的周期内给该相三个定子齿极绕组同时励磁的方法，实现了电机的悬浮旋转。

除此之外，一些学者还从改变电机定子和转子结构的角度出发，研究了一些结构较为特殊的BSRM。文献［17］提出一种将SRM转子与磁轴承复合在一起的结构。该种结构的电机从转子轴向上看可分为SRM转子与磁轴承转子两个部分，其中叠片的结构为凸极形的是SRM转子，而圆柱形的则为磁轴承转子，通过控制开通相绕组电流，产生所需要的悬浮力与转矩。另外还有一种宽窄齿相隔分布结构的8/10极单绕组BSRM。这种结构的电机采用双相导通模式，每次导通宽齿绕组和窄齿两套绕组，宽齿四套绕组为悬浮力相，窄齿两套绕组为转矩相，由于悬浮力和转矩分别由不同的齿提供，因而该结构的BSRM某种程度上实现了转矩和悬浮力的解耦控制。

本文主要是基于双绕组BSRM的研究已经相对完善，同时通过单绕组BSRM和双绕组BSRM磁势相等的原则，建立单、双绕组BSRM之间的联系，并解算出电机各绕组电流，为以后单绕组BSRM的悬浮控制奠定基础，并分析了单、双绕组BSRM内在联系，对比了其工作区域，指出在相同匝数的情况下，单绕组BSRM工作区域比双绕组BSRM大。

1 双绕组BSRM工作原理

双绕组BSRM在普通SRM的定子齿极上额外增加了一套绕组，其基本结构如图1所示。图中，Nma表示主绕组，且一相四个定子齿极上的主绕组相串联，主要用来提供转矩;Nsa1、Nsa2分别表示α和β方向上的悬浮绕组，其一相正对方向上的两个悬浮绕组相串联，用来提供不平衡的径向力。ima为主绕组电流，其所产生的磁通由粗实线表示，isa1、isa2分别为α和β方向上悬浮绕组的电流，由其产生的磁通用虚线表示，下标“+”、“－”则表示电流的流入与流出。A、B、C三相的绕组结构相同，但B、C两相与A相分别有－30°和+30°的空间位置差。将A相作为基准，定义直角坐标系，横轴用α(a1)表示，纵轴用β(a2)表示，B相和C相的坐标轴定义与A相相同。

若A相通入图示的电流，那么气隙1处的电流ima和isa1将产生相同方向的磁场，其磁密将会增大，气隙2处则相反。这样，叠加之后的磁场将会沿着α方向产生一个向右的磁拉力Fα。此时若不改变主绕组的电流，而是反向通入悬浮绕组的电流isa1，则产生的磁拉力将会反向。同理，沿着β方向同样能够产生径向的磁拉力Fβ。这样转轴的位移采用负反馈控制之后，就能够控制悬浮力的大小以及方向，从而使转轴悬浮旋转。

B、C两相的原理与A相完全相同，只需在控制的过程中对B相和C相做一定的坐标变换即可。

图1 双绕组BSRM悬浮力产生原理图

2 双绕组BSRM数学模型

目前大都采用虚位移的方法建立BSRM的数学模型，主要可分为以下几个步骤:(1)将磁场进行分割，求出气隙磁导;(2)运用等效磁路的方法得出一相的电感矩阵，同时以该矩阵求解出电机磁场的储能;(3)依据机电之间能量转换的基本原理，将磁场的储能对转轴的位置角以及径向位移分别求偏导，最终得出转矩表达式和悬浮力的表达式［20］。在不考虑漏磁通以及磁路饱和的情况下，悬浮力的数学表达式如下:

上述表达式并未将α方向和β方向上径向悬浮力之间的耦合因素考虑进去。若考虑悬浮力之间的耦合因素，则要对传统的数学模型进行改进［18］，改进后的模型将边缘的磁通路径近似成椭圆形，然后分割求取气隙的磁导，有效解决了绕组电感顶部凹陷的问题。基于改进后的数学模型，悬浮力和转矩的数学表达式可以分别表示:

上述表达式中的Kf1和Kf2以及J(θ)是只与转子的位置角以及电机的自身机械参数相关的函数，文献［22］有相关公式具体的推导过程。该模型更为准确地描述了双绕组BSRM。

3 单绕组BSRM工作原理

与双绕组BSRM不同，单绕组BSRM定子齿上无需额外增加绕组，只需给一相四个齿极绕组通以不同的电流，就能使转轴悬浮旋转。图2展示了12/8极单绕组BSRM的基本结构。

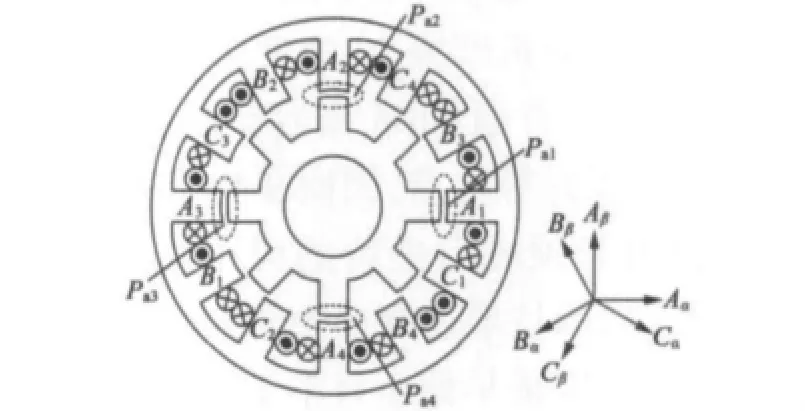
图2 单绕组BSRM结构示意图

当A1绕组电流大于A3绕组电流时，A1处磁密大于A3处磁密，其合成之后的磁场就会沿着α方向产生一个向右的磁拉力Fα。若A3绕组电流大于A1绕组电流，则产生的径向力方向将相反。依据同样的原理，沿着β方向同样能够产生径向的磁拉力Fβ。类似地，B相、C相亦是如此。因而，只需对转轴的位移采用负反馈控制，就可以使径向磁拉力的大小以及方向发生改变，从而达到转轴悬浮旋转目的。

由此可见，单绕组BSRM和双绕组BSRM本质上都是通过改变径向相对齿极气隙处磁密的不同来改变悬浮力的大小和方向。

4 单、双绕组BSRM等效原理

图3(a)、图3(b)分别为单绕组和双绕组BSRM单相等效磁路图。

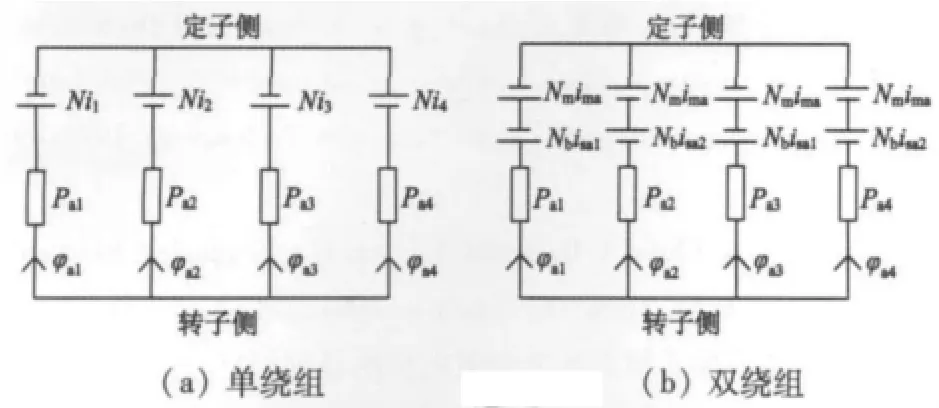
图3 BSRM单相等效磁路图

等效的前提是，双绕组单个齿极总匝数和单绕组单个齿极总匝数相等。根据磁势相等的原则，可得:

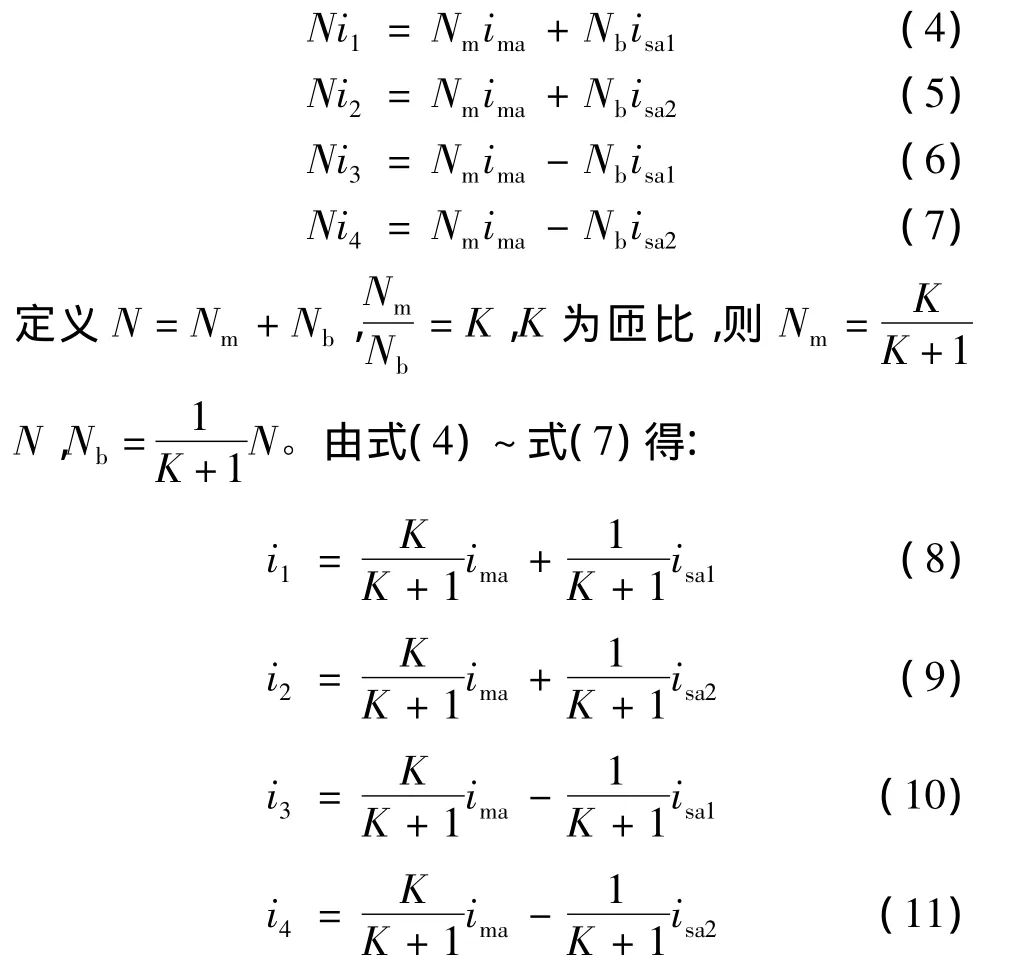
由双绕组公式［18］知，转矩T和悬浮力F表达式可改写成:

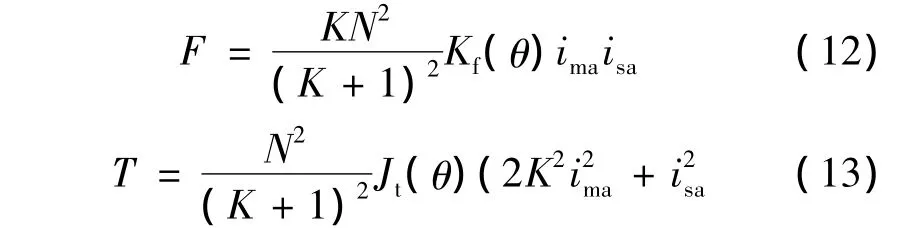
由式(4)～式(13)解得:

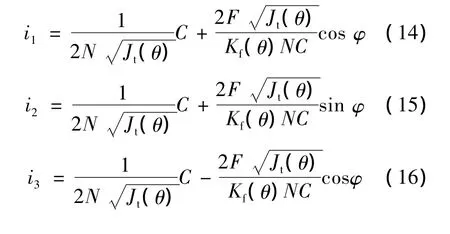
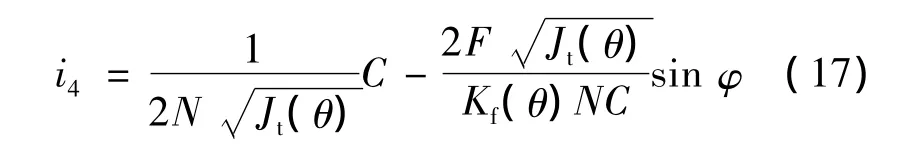
5 仿真验证

为验证等效原理的正确性，本文选取总匝数为18，主绕组的匝数为9、悬浮绕组的匝数同样为9的单、双绕组BSRM仿真参数，同时给出了一组悬浮力F以及转矩T(绝对值)，利用双绕组公式计算出主绕组电流和悬浮绕组电流，再利用等效原理计算出单绕组各绕组电流，分别用Ansys软件进行有限元仿真。

图4(a)为有限元转矩的仿真结果曲线，T为给定转矩，T1为双绕组仿真结果，T2为φ=30°时的单绕组仿真结果，T3为φ=45°时的单绕组仿真结果。从图中可以看出，单、双绕组BSRM转矩完全重合，只是在转子位置角为15°时，仿真转矩与给定转矩存在偏差，这是由于双绕组理论本身在15°时的不够精确导致，但等效依然正确。图4(b)为悬浮力的仿真结果曲线，F为给定的悬浮力，F1为双绕组仿真结果，F2为φ=30°时的单绕组仿真结果，F3为φ=45°时的单绕组仿真结果。

为进一步验证等效原理的正确性，本文用MATLAB软件搭建单双绕组BSRM仿真模型，选取总匝数为30，主绕组和悬浮绕组匝数都为15，给定悬浮力Fα=60、Fβ=40，主绕组电流为15 A的单、双绕组BSRM电机仿真参数。图4(c)、图4(d)分别为单、双绕组BSRM悬浮力仿真结果，图4(e)为单绕组BSRM电流仿真波形，图4(f)为双绕组BSRM 电流仿真波形，图中的为等效后的单绕组电流。图4(g)、图4(h)分别为单、双绕组BSRM转矩仿真波形。从仿真结果可以看出，无论单绕组BSRM还是双绕组BSRM，悬浮力跟踪良好，在磁势相等的情况下，单双绕组BSRM输出的悬浮力和转矩一致。

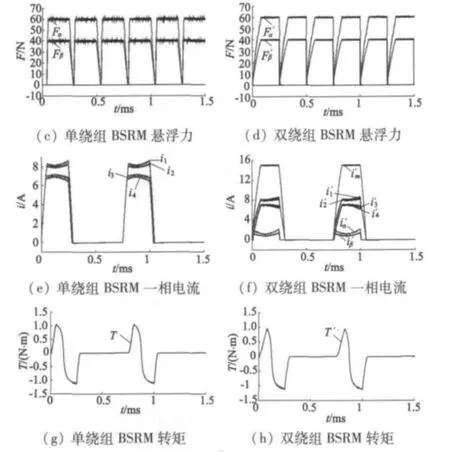
图4 单、双绕组BSRM仿真参数

基于以上有限元分析和MATLAB动态建模仿真结果，无论转矩还是悬浮力，单绕组BSRM的悬浮力和转矩分布均与双绕组BSRM结果吻合，从而验证了等效原理的正确性和有效性。

6 工作区域比较

为了对比单、双绕组BSRM的工作区域，选取总匝数为18，双绕组BSRM主绕组和悬浮绕组匝数分别取9、9(K=1)和 12、6(K=2)，绕组限流值为 20 A，图5为单、双绕组BSRM工作区域对比图。

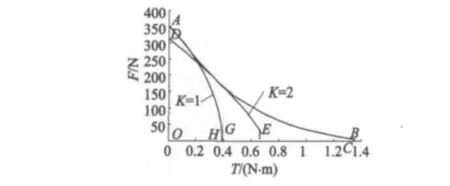
图5 工作区域的比较

图中区域OABC为单绕组工作区域，OAGH为主绕组和悬浮绕组都为9的双绕组BSRM工作区域，ODEF为主绕组12，悬浮绕组为6的双绕组BSRM工作区域。可以看出，在总匝数一定的情况下，单绕组BSRM比双绕组BSRM工作区域大，这是单绕组BSRM相对于双绕组BSRM最明显的优势。

7 结 语

等效原理利用现有双绕组BSRM的理论成果，能够精确计算出单绕组BSRM悬浮和旋转所需的各绕组电流，有助于继承和发展双绕组BSRM的研究体系，为今后单绕组BSRM控制策略的研究提供新的视角。同时，单绕组BSRM比双绕组BSRM工作区域大，更具研究价值。

［1］Chiba A，Fukao T.super high speed electical machine［C］//Power Engineering society general meeting.2004，6(2):1272－1275.

［2］Takemoto M，shimada K，Chiba A，et al.A design and characteristics of switched reluctance type bearingless motors［C］//4th International Symposium on Magnetic Suspensio Techonology.1998:49－63.

［3］Takemoto M，Chiba A.Improved Anaiysis of a Bearingless Switched Motor［J］.IEEE Trans.Ind.Applicat.2001，37(1):26－34.

［4］曹鑫.12/8极无轴承开关磁阻电机的研究［D］.南京:南京航空航天大学，2010.

［5］Choi B B，Siebert M.A bearingless switched reluctance motor for high specific power applications［C］//42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference ＆ Exhibit.2006.

［6］Liu W T，Yang S M.Modeling and control of a self－bearing switched reluctance motor［C］//2005 Industry Applications Conference，14th IAS Annu Meeting.Princeton:IAS，2005:2720－2725.

［7］Lin F C，Yang S M.Self－bearing control of a switched reluctance motor using sinusoidal currents［J］.IEEE Trans.Power Electron.，2007，22(6):2518－2526.

［8］Chen L，Hofmann W.Analytically computing winding currents to generate torque and levitation force of a new bearingless switched reluctance motor［C］//12th International Power Electronics and Motion Control Conference.2006:1058－1063.

［9］Chen L，Hofmann W.Performance characteristics of one novel switched reluctance bearingless motor drive［C］//Power Conversion Conference 2007(PCC ＇07).2007:608－613.

［10］Chen L，Hofmann W.Design procedure of bearingless high－speed switched reluctance motors［C］//SPEEDAM 2010，Pisa Italy.2010.

［11］Wang H，Lee D H，Ahn J W.Calculation of suspending force for new bearingless switched reluctance motor［C］//Proceedings of the 11th International Symposium on Magnetic Bearings(ISMB－11).Nara，Japan，2008:366－372.

［12］Wang Huijun，Park T－H，Kim T－H，et al.Novel bearingless switched reluctance motor with hybrid stator poles:Concept，A-nalysis，Design and Experimental Verification［C］//The 11th International Conference on Electrical Machines and Systems.2008:3358－3363.

［13］Lee D H，Wang Huijun，Ahn J W.Modeling and control of novel bearingless switched reluctance motor［C］//IEEE Energy Conversion Congress and Exposition 2009(ECCE2009).2009:276－281.

［14］Guan Zhongyu，Lee D H，Ahn J W，et al.A compensation strategy of suspending force in hybrid type stator pole bearingless switched reluctance motor［C］//2011 International Conference on Electrical Machines and Systems(ICEMS).2011.

［15］Xu Zhenyao，Lee D H，Zhang Fengge，et al.Hybrid pole type bearingless switched reluctance motor with short flux path［C］//2011 International Conference on Electrical Machines and Systems.2011.

［16］Wei Peng，Lee D H，Ahn J W.Design and analysis of double stator type bearingless switched reluctance motor［J］.Transactions of the Korean Institute of Electrical Engineers，2011，60:746－752.

［17］Morrison C R，Siebert M W，Ho E J.Electromagnetic forces in a hybrid magnetic－bearing switched－reluctance motor［J］.IEEE Trans.on Magnetics，2008，44(12):4626－4638.

［18］邓智泉，杨钢，张媛，等.一种新型的无轴承开关磁阻电机数学模型［J］.中国电机工程学报，2005，25(9):139－146.

［19］李倬，葛宝明.一种改进的无轴承开关磁阻电机数学模型［J］.电机与控制学报，2009，13(6):850－856.

［20］吴建兵，孙玉坤，吉敬华.磁悬浮开关磁阻电动机研究［J］.微电机，2007，40(7):79－85.

［21］孙玉坤，吴建兵，项倩雯.基于有限元法的磁悬浮开关磁阻电机数学模型［J］.中国电机工程学报，2007，27(12):33－40.

［22］杨钢.无轴承开关磁阻电动机的基础研究［D］.南京:南京航空航天大学，2008.