基于楔形基函数的点插值法

童小红, 胡 钢

(西安理工大学 理学院, 陕西 西安 710054)

0 引言

目前，无网格算法求解偏微分方程数值解是近年来迅速兴起的一种新型的、高效的数值方法[1-7].无网格算法中，相对于径向基函数研究，楔形基函数无论在理论研究方面还是实际应用方面都非常少[8-10].

文献[11]讨论了二维空间中楔形基函数插值问题的可解性,构造允许向量并且利用Kriging泛函的性质给出插值问题的误差估计.文献[12]构造了基于楔形基函数的加权最小二乘无网格方法，并应用于弹性静力学问题.最近，文献[13]讨论楔形基的配点无网格法，并给出了数值解的存在惟一性.文献[14,15]分别将楔形基函数无网格法应用于求解对流扩散方程.但在现有的文献中，基于楔形基函数的点插值方法还没有相关研究.考虑到点插值法在计算方面具有简单实用的特点，并针对热传导问题，本文提出了一种新的无网格方法—楔形基点插值法.通过数值算例验证该算法切实可行，而且能够达到满意的收敛效果.

1 楔形基点插值无网格法

考虑热传导方程的边值问题：

(1)

其中x= (x, y)T，Ω是有界矩形区域，光滑边界∂Ω，2为Laplace算子，k为常数.

1.1 楔形基函数近似

定理1[1]如果φ(·)不是多项式，则楔形基{φ(cTx+d)}可以逼近几乎所有的函数.

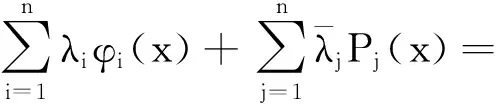
(2)

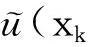
(3)

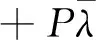
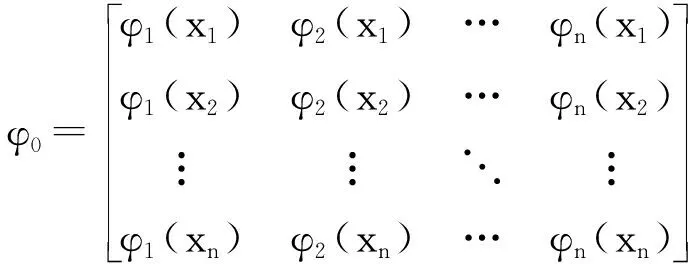
根据楔形基函数的性质，有φi(xj)=φj(xi)，所以Φ0为对称矩阵.

1.2 数值算法的构造

采用点插值法，于是由(1)式得到在时间层tn的离散：

(4)

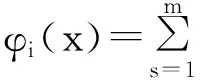
为保证近似函数惟一性，对系数附加如下条件：

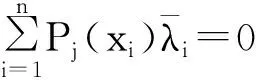
(5)

写成矩阵形式

(6)

G为(6)式中时间层t=tn-1时右端项的值组成的向量.

1.3 数值解的存在惟一性

定理2[11]若楔形基函数Φ(x)的傅立叶变换F[Φ](ω)几乎处处大于零，则插值矩阵Q是正定的.

定理3[13]函数Φ(x)=φ(a·x)是正定函数的充分必要条件是其傅里叶变换F[Φ](ω)几乎处处大于零.

定理4若楔形基函数Φ(x)是正定的，则楔形基函数点插值法求解(1)式有惟一的数值解.

证明：首先证明Φ是正定的.∀ζ≠0∈RN,

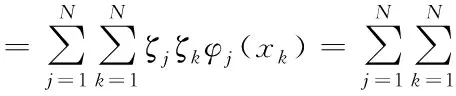
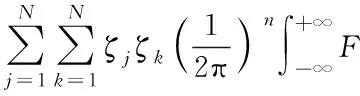
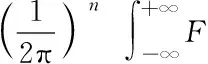
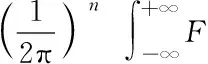
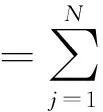
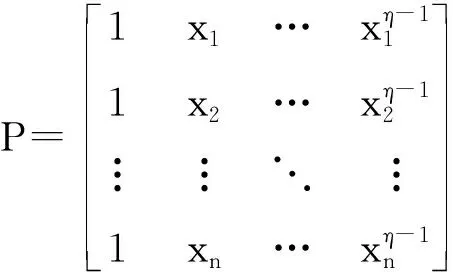
P的前η行构成η级Vandermonde行列式，由于节点的互异性，可知前η行为其最大线性无关组，故rank(P)=η.于是可对P进行行初等变换：P1=Q1P(Q1是一个n×n可逆矩阵)，使P1的线性无关组位于前η行，并且满足后n-η行的元素值皆为0，有

PTΦ-1P=(Q1-1)P1TΦ-1Q1-1P1=

P1T(Q1-1)TΦ-1Q1-1

P1=P1T((Q1-1)TΦ-1Q1-1)P1

(7)

Q1可逆，故(Q1-1)TΦ-1Q1-1可逆.对P1进行分块：P1T=[P20]，显然P2为η×η可逆矩阵，所以

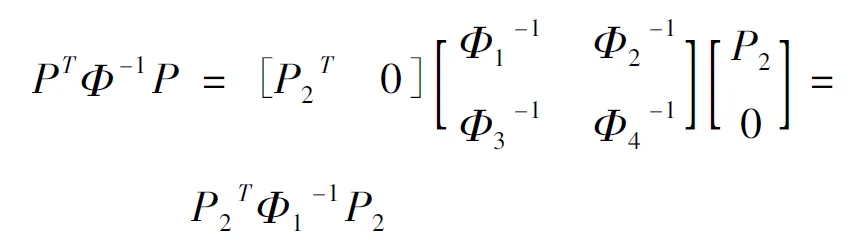
Φ对称正定，其合同矩阵(Q1-1)TΦ-1Q1-1对称正定，则Φ1对称正定，P2TΦ1-1P2对称正定，故PTΦ-1P对称正定.所以在时间层t=tn(5)存在惟一数值解.因此由定理3知，若楔形基函数正定， (4)存在惟一的数值解.

2 数值算例和分析

算例1 考虑一维初边值问题：

(8)

其中Ω={x|0≤x≤2}，解析解为u(x,t)=exp(0.001t)x(1-x).u0、g1和gN由解析解确定.采取L2误差估计.取IMQ为楔形基函数.用L2范数进行误差估计.计算方向在圆盘上取得，方向为：as=(cos(θs),sin(θs)),θs=(s-1)π/9，s=1,2,…,m；时间步长Δt=0.01，取m=4.计算结果如表1.

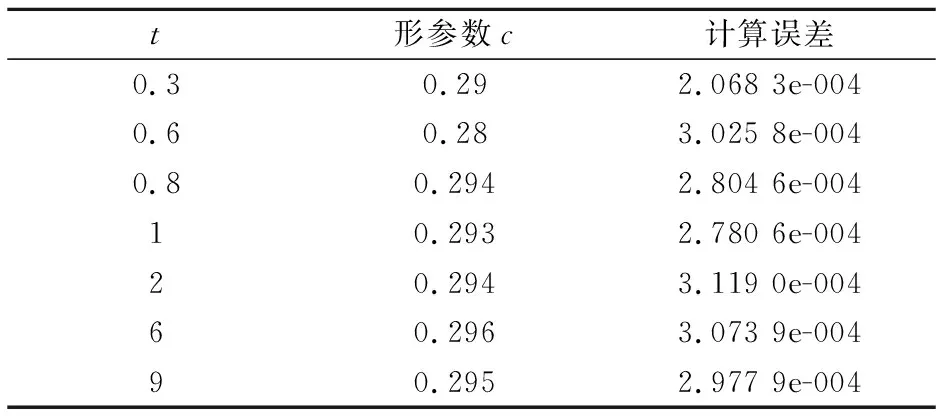
表1 本文方法数值解的误差计算

通过表1，我们可以看到楔形基点插值法求解一维热传导方程能得到满意的收敛效果.

图1～图4分别是本文方法、径向基点插值法、有限差分法和有限元法进行计算结果.通过图1和图2可以看到楔形基点插值法和径向基点插值法一样，都能达到满意的收敛效果.又将计算时间和计算误差进行了比较，结果如表2.

表2 本文方法计算误差与其他数值

由表2我们得到结论：本文楔形基点插值无网格法和径向基无网格法都能达到满意的收敛效果；与有限差分法和有限元法相比，本文数值算法在计算误差方面有明显的优势.通过表1和表2发现，影响本文楔形基无网格点插值法数值解精度的因素有插入节点数的取法和形参数的选取.

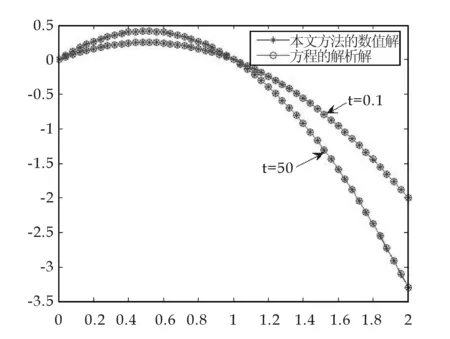
图1 本文的楔形基点插值法数值解

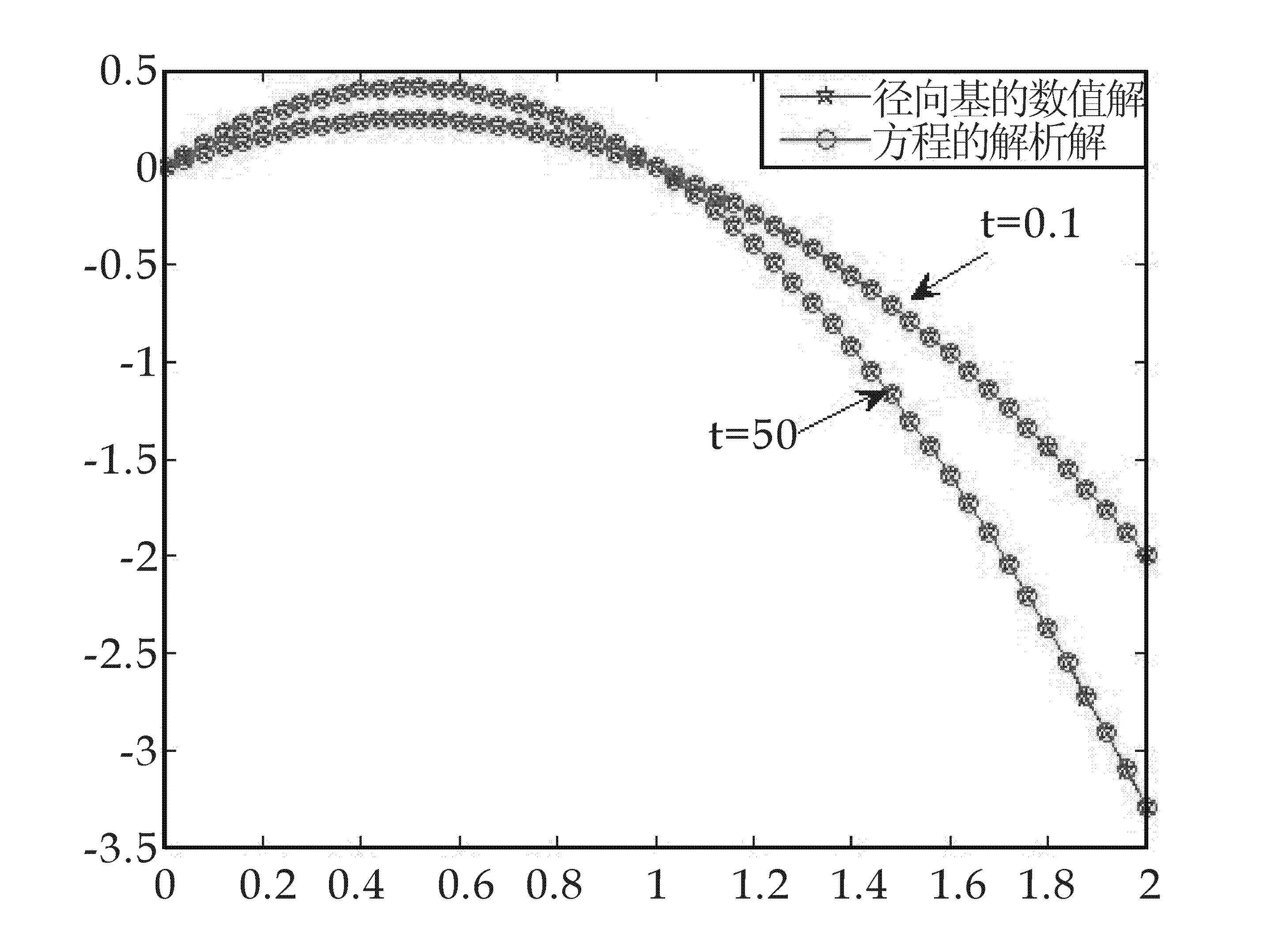
图2 径向基点插值法数值解

图3 有限差分法数值解

算例2 考虑二维初边值问题：

(9)

其中Ω={(x,y)|0≤x≤1,0≤y≤1} ,解析解为u(x,y,t)=tsin(πx)sin(πy).u0和g由解析解确定；我们采取L2误差估计.取MQ为楔形基函数.

图4 有限元法数值解

计算方向在圆盘上取得，方向为：as=(cos(θs),sin(θs)),θs=(s-1)π/(m-1), s=1,2,…,m；时间步长Δt=0.01，取m=9,10,11,12,13,14,15,16.误差计算结果如图5～图10、表3和表4.

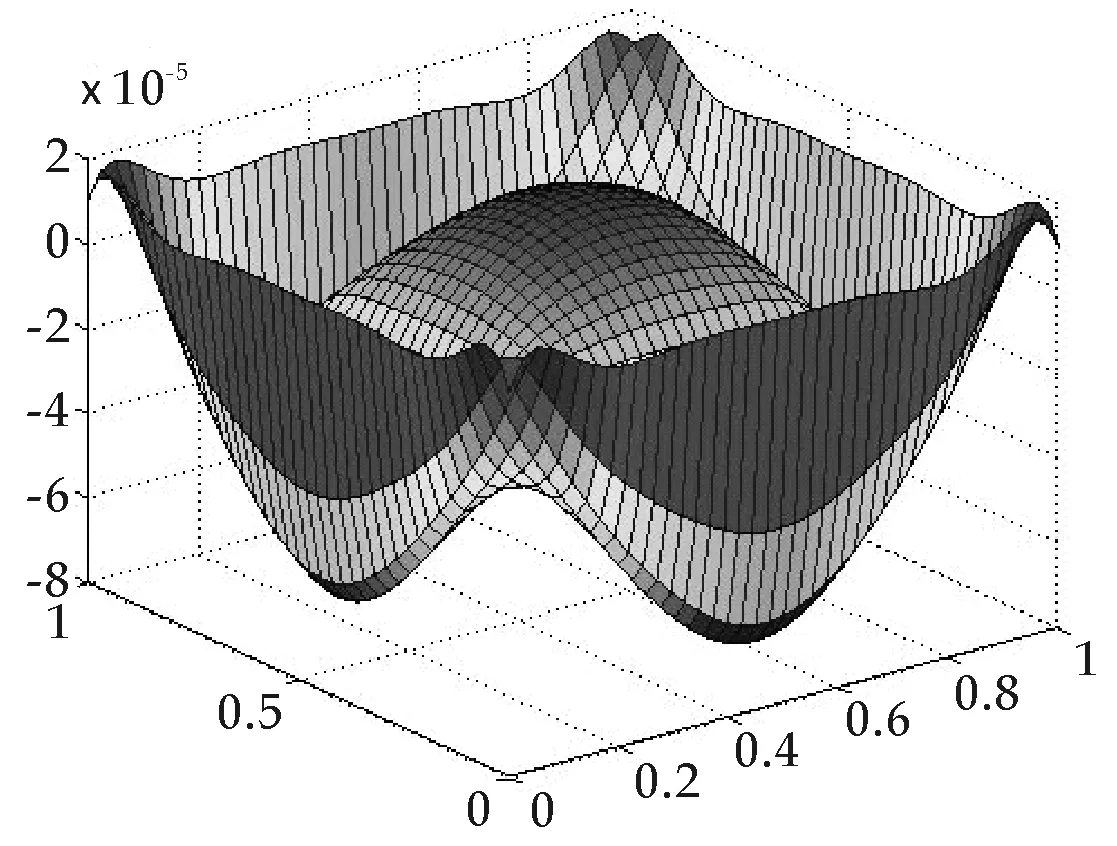
图5 本文数值解误差t=0.5,m=9

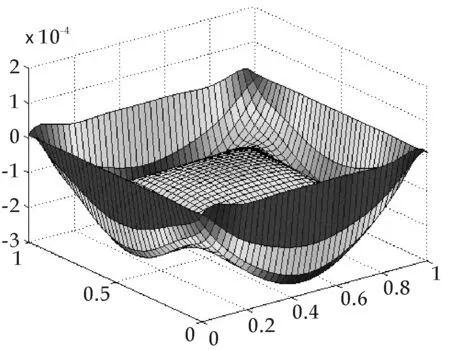
图6 本文数值解误差t=1.2,m=10

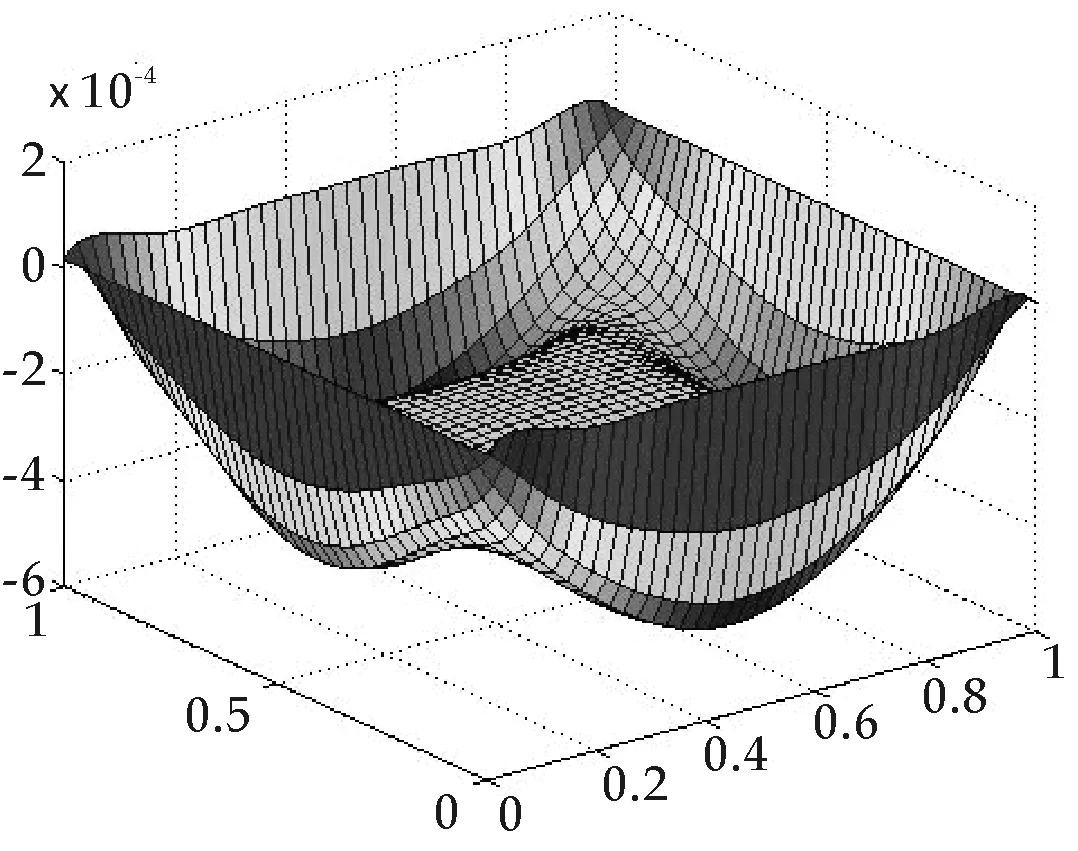
图7 本文数值解误差t=1.8,m=12

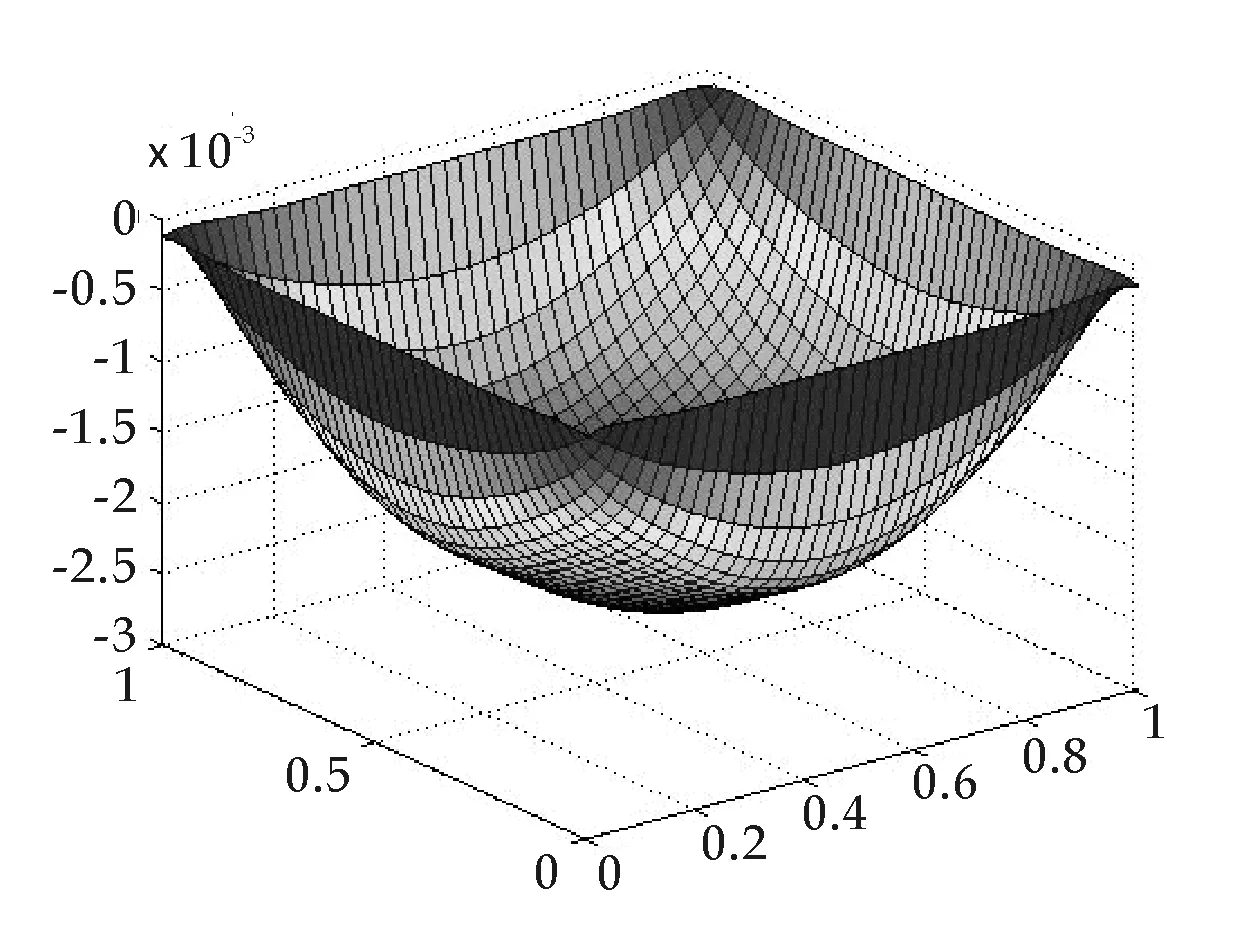
图8 本文数值解误差t=3.2,m=14

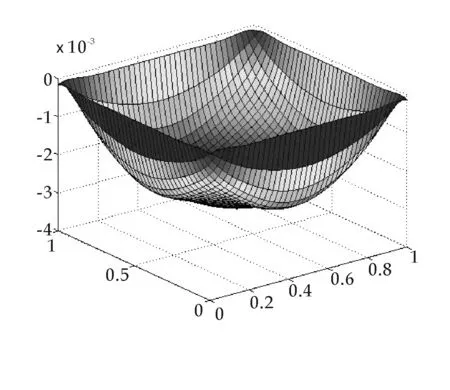
图9 本文数值解误差t=5.5,m=14

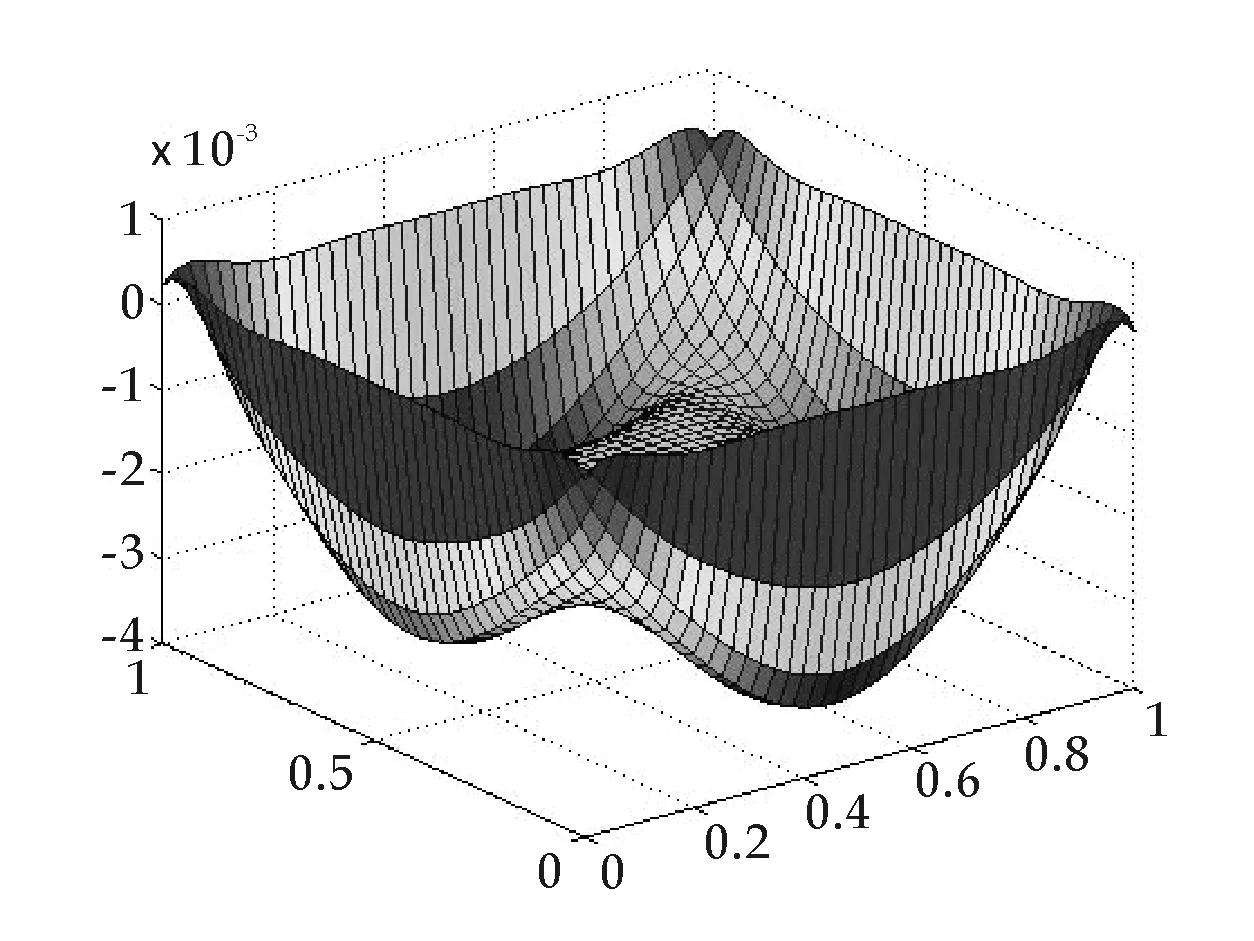
图10 本文数值解误差t=16,m=16

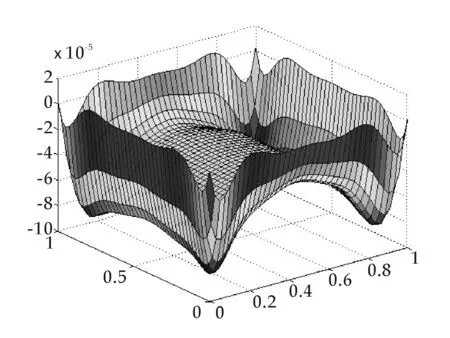
图11 本文数值解误差t=0.4,m=9

tcm=9计算误差 m=11计算误差m=13计算误差m=15计算误差0.51.61.138 7e-0046.505 5e-0044.694 4e-0042.611 3e-0040.81.569.697 0e-0057.035 8e-0044.425 2e-0042.287 8e-00411.552.467 7e-0049.399 7e-0041.829 0e-0041.036 8e-0031.51.552.997 8e-0048.783 7e-0041.871 1e-0041.056 0e-00331.61.076 6e-0041.867 7e-0044.372 9e-0048.997 8e-00451.552.606 2e-0049.166 4e-0041.830 5e-0041.021 8e-003151. 54.310 5e-0042.591 4e-0041.854 0e-0041.118 5e-003

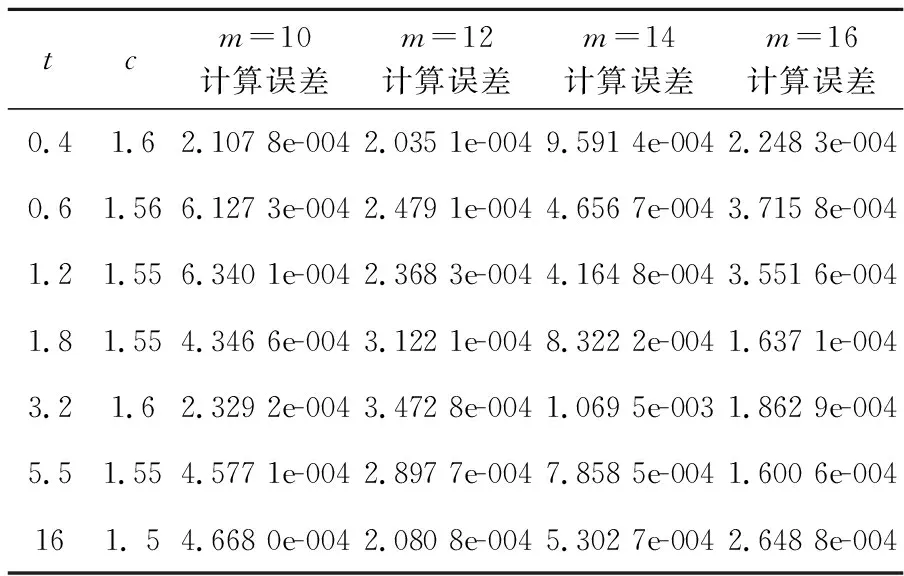
表4 本文方法数值解的误差计算结果

由图5～图10我们看到，本文无网格方法具有很好的收敛效果.再由表3和表4的数值分析我们发现，影响本文楔形基无网格配点法数值解精度的因素包括方向的确定.

当时间步长Δt= 0.02，取m= 9,10,11,12.取Gaussians为楔形基函数，计算结果如表5和图11～图14.

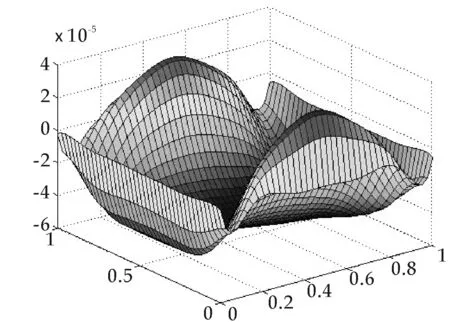
图12 本文数值解误差t=0.4,m=10

图13 本文数值解误差t=0.4,m=11

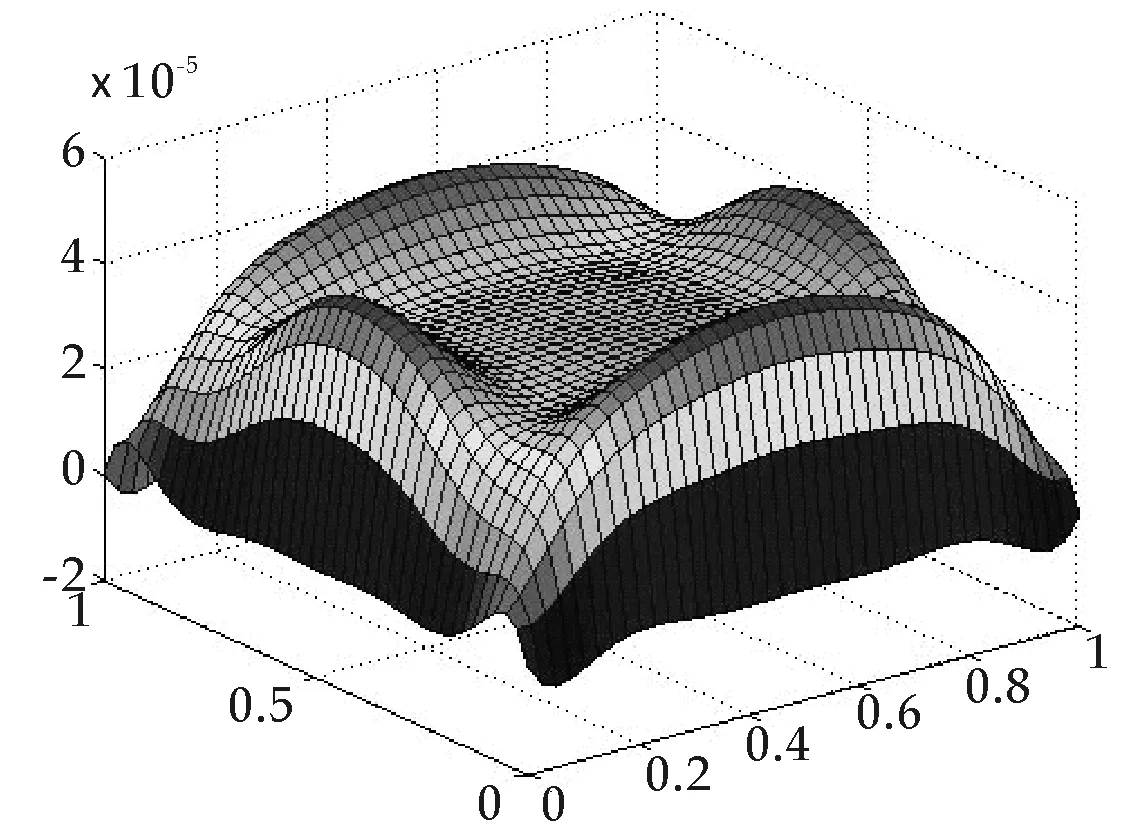
图14 本文数值解误差t=0.4,m=12

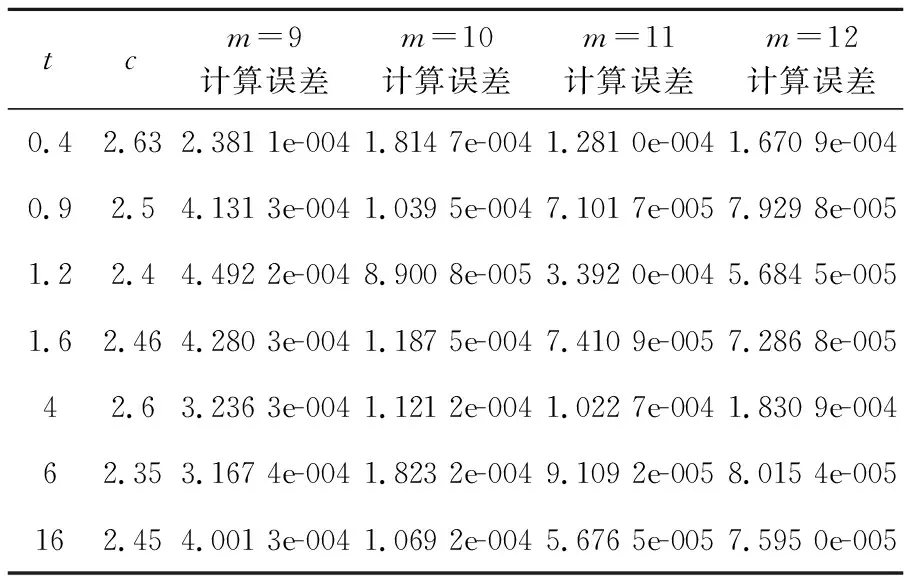
tcm=9计算误差 m=10计算误差m=11计算误差m=12计算误差0.42.632.381 1e-0041.814 7e-0041.281 0e-0041.670 9e-0040.92.54.131 3e-0041.039 5e-0047.101 7e-0057.929 8e-0051.22.44.492 2e-0048.900 8e-0053.392 0e-0045.684 5e-0051.62.464.280 3e-0041.187 5e-0047.410 9e-0057.286 8e-00542.63.236 3e-0041.121 2e-0041.022 7e-0041.830 9e-00462.353.167 4e-0041.823 2e-0049.109 2e-0058.015 4e-005162.454.001 3e-0041.069 2e-0045.676 5e-0057.595 0e-005

由表5的数值和图11～图14分析我们发现，影响本文无网格法数值解精度的因素有时间步长的选取和基函数的选取.

3 结论

本文所构造的楔形基点插值无网格法求解对热传导方程切实可行，该方法是真正的无网格方法，并且该无网格法仍具有非常高的计算精度.本文无网格法数值解的计算精度与基函数的形参数的选取、插入节点的取法、时间步长的选取、基函数的选取、方向的选取都相关.

[1] 吴宗敏.径向基函数、散乱数据拟合与无网格偏微分方程数值解[J].工程数学学报,2002,19(2):1-12.

[2] 张 雄,宋康祖,陆明万.无网格法研究进展及其应用[J].计算力学学报,2003,20(6):730-742.

[3] Zhang X,Song K Z,Lu M W,et al.Meshless methods based on collocation with radial basis functions[J].Computational Mechanics,2000,26(4):333-343.

[4] Duan Y,Tan Y.Meshless collocation method based on Dirichlet-Neumann substructure iteration[J].Applied Mathematics and Computation,2005,166(2):373-384.

[5] Wang J G,Liu G R.A point interpolation meshless method based on radial basis functions[J].International Journal for Numerical Methods in Engineering,2002,54(11):1 623-1 648.

[6] 张宏伟,李美香,李卫国.关于配点型无网格法边界条件处理技术[J].大连理工大学学报,2010,50(4):614-618.

[7] 张 林,欧阳洁,张文彬,等.基于无网格稳定化方案求解非稳态强对流问题的自适应节点加密技术[J].计算力学学报,2010,27(3):446-450.

[8] 张立伟.有限平面波的线性组合的楔形基函数逼近[J].山东大学学报(理学版),2006,41(6):89-92.

[9] 王志刚, 秦新强, 党发宁, 等.楔形基无网格法解的存在唯一性[J].山东大学学报(理学版),2010,45(2):44-49.

[10] 田双亮,房保言,王志刚.基于楔形基函数的微分博弈两点边值问题的逼近[J].山东大学学报(理学版),2011,46(8):38-41.

[11] 张立伟.楔形基函数插值及其误差估计[J].复旦学报(自然科学版),2005,44(2):302-306.

[12] 署恒木,黄朝琴,李翠伟.基于楔形基函数的一种新型无网格法[J].中国石油大学学报,2008,32(3):109-113.

[13] Wang Z,Qin X,Wei G,et al.Meshless method with ridge basis functions[J].Applied Mathematics and Computation,2010,217(5):1 870-1 886.

[14] 童小红, 秦新强.一种新的求解对流扩散边值问题的无网格方法[J].计算力学学报,2012,29(5):716-720.

[15] 王丽华,秦新强,王全九.对流占优扩散方程的特征线楔形基无网格法[J].数学杂志,2012,32(1):99-107.