声软障碍在两层介质中声波散射问题的数值解
2013-01-29荣翠莲王连堂
荣翠莲, 王连堂
(西北大学 数学系, 陕西 西安 710127))
0 引言
声波散射和传播问题在医学成像、地理勘探、非破坏性检测等领域中有着广泛的应用,一直都是数学物理领域的研究热点.古典声波散射理论有两个基本问题,一是时间调和声波在不可穿透障碍散射的问题,另一个是时间调和声波在非均匀介质中的散射问题.对于均匀介质中声波散射的各问题,如混合边界、开弧等大多都得到了很好地解决[1-4],而对非均匀介质的研究相对较少.分层介质是非均匀介质中一种简单而有实际意义的情况.文献[5]从理论上给出了不可穿透障碍在两层介质中声波散射正问题的适定性及反问题的唯一性,本文主要利用边界积分方程和Nystrom法给出此类正问题的数值算法,并给出不同的数值算例.

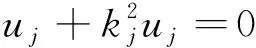
(1)
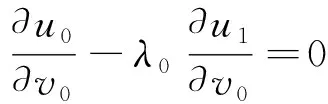
(2)
u1=0,x∈Γ1
(3)
这里,波数kj=wj/cj,wj为介质Dj中波的频率,cj为波速.λ0是D0,D1中两种介质密度之比,它为正常数.外部全场u0可以分解为u0=ui+us,其中ui表示入射平面波,比如ui=eik0x·d,us表示散射场,us满足Sommerfeld辐射条件,
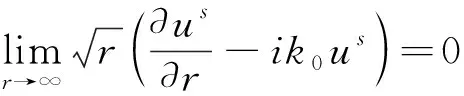
(4)
此外,每个散射场的辐射解有如下的外部渐进性:
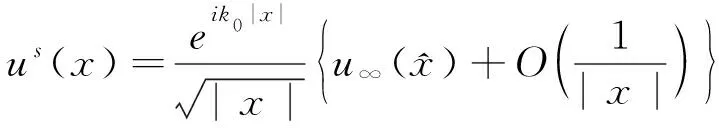
1 正散射问题的解
定理1 正散射问题(1)~(4)至多有一解[5].
对于正散射问题解的存在性,我们利用位势理论将其转化为边界积分方程组.因为Helmholtz方程的任何一个解均可表示为单、双层位势的组合,我们先定义单双层位势.设Γl,Γj均为有界封闭曲线,φ为可积函数,则积分
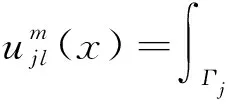
(5)
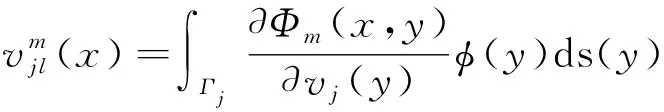
(6)
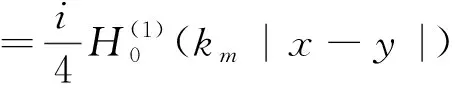
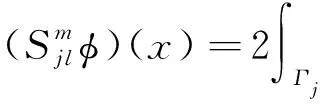
(7)
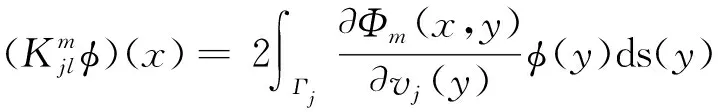
(8)
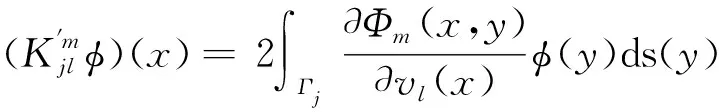
(9)
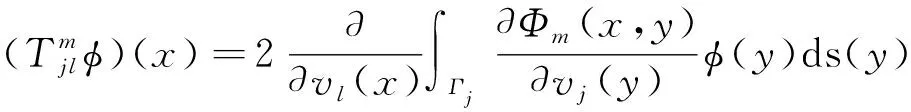
x∈Γl
(10)
这里,j,l,m={0,1}.用C0,α(Γj)和C1,α(Γj)表示Hölder连续函数空间和Hölder连续可微函数空间.当j≠l时,上述算子从C(Γj)→C0,α(Γj)和从C0,α(Γj)→C1,α(Γj)都是紧的[7].
用如下形式的单双层位势组合来表示散射场us和u1:
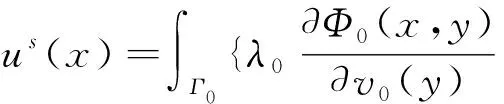
Φ0(x,y)φ(y)}ds(y),
x∈D0
(11)
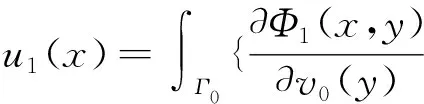
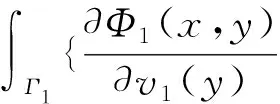
x∈D1
(12)
其中ψ,φ,χ是三个待定的函数,η≠0是耦合参数.运用边界条件(2)、(3)及单双层位势的跳跃关系,不难推出下面的边界积分方程组:
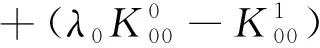

(13)
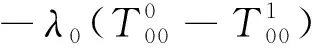
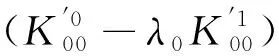
(14)
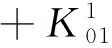
(15)
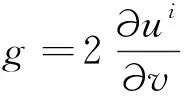
X=(ψ,φ,χ)′,C=(f,g,0)′,I为恒等算子.所以,方程组可简记为:
(E+A)X=C
因为E是有界逆算子,A为紧算子,由Riesz-Fredholm理论知方程组有唯一解[8].因此,我们有以下结论:
定理2 如果k12不是负的Laplace算子的Dirichlet特征值,则正散射问题有唯一解.
由Hankel函数的渐进性知,单双层位势组合所对应的远场模式为:
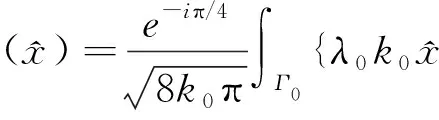
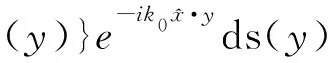
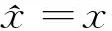
2 数值算法
Γj:{zj(t)=(zj1(t),zj2(t)),0≤t≤2π},j={0,1},
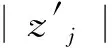
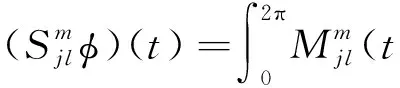
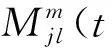

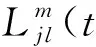
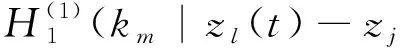
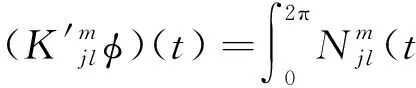
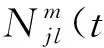
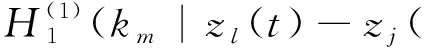
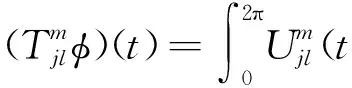
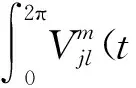
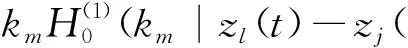
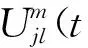
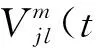
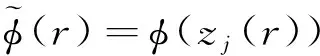
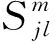
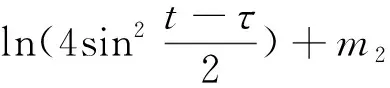
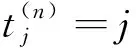
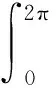
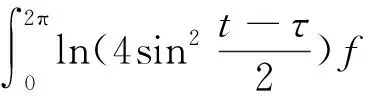
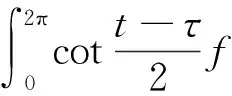
其中:
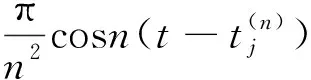
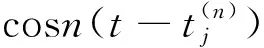
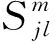
(λ0+1)ψ(z0(ti))+
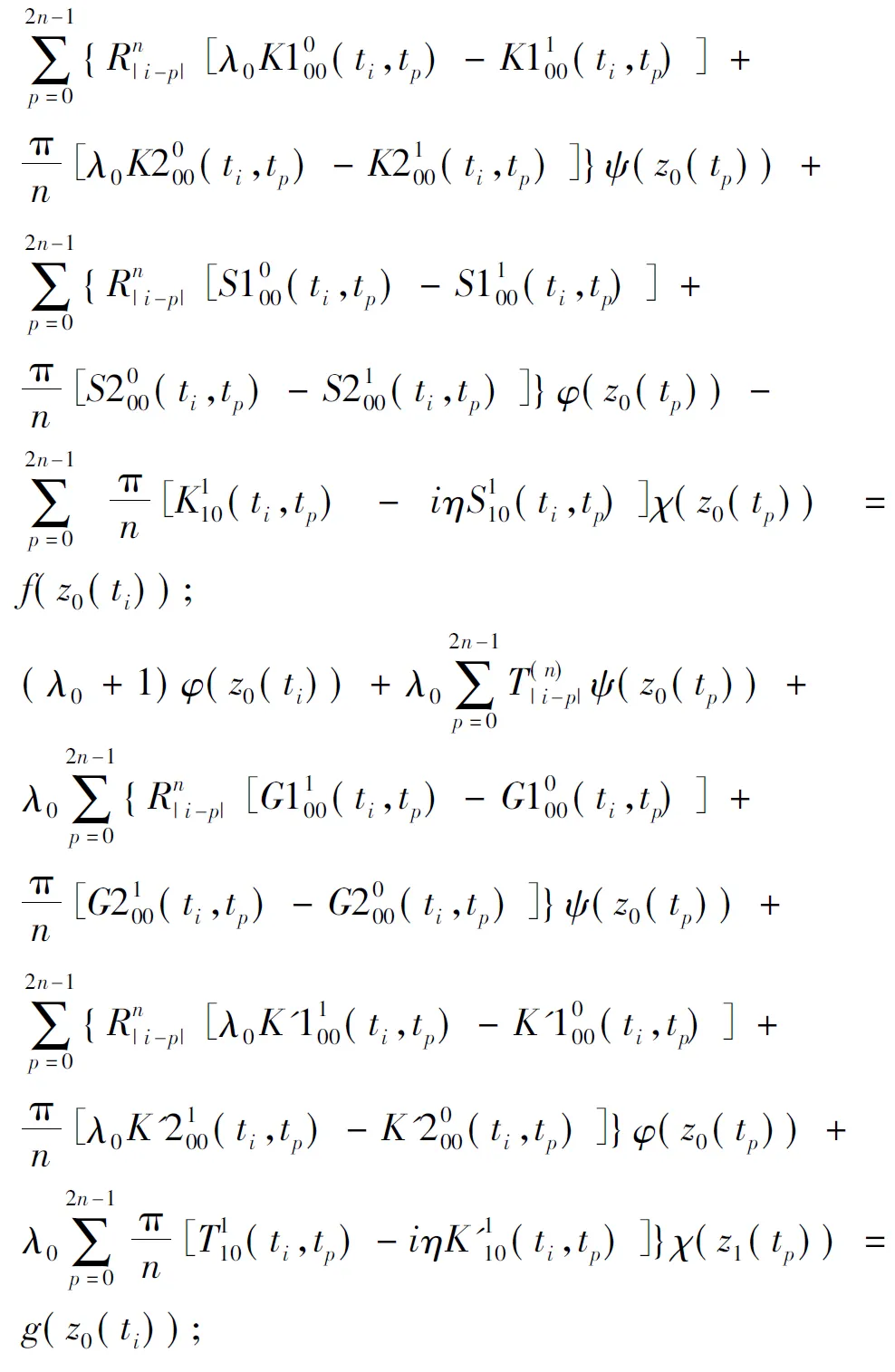
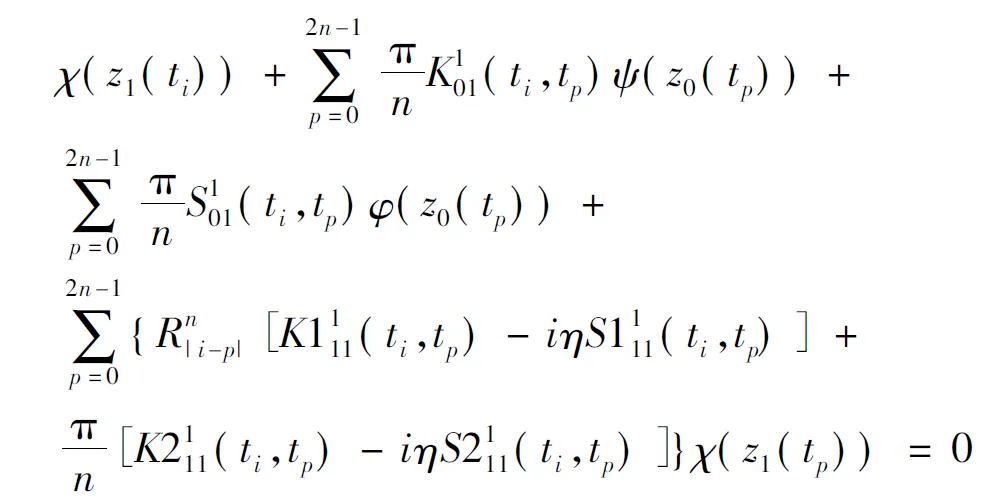
这里
(-1)|i-p|π
p=0,1,…,2n-1
式中,G1(t,τ),G2(t,τ)为超奇异T算子核裂解得出,具体可参考文献[9],这里只是加上边界标号.
3 数值算例
在数值计算时,取定入射波为ui=eik0x·d,其中d=(1,0)表示入射方向,参数η=k1.下面给出具体的数值算例的求值结果.
例1 外边界曲线Γ0,内边界曲线Γ1,

t∈[0,2π];
Γ1:z1(t)=(cost,sint),t∈[0,2π],区域内波数为k0=0.5,k1=1.远场模式u∞(d)和u∞(-d)的数值结果如表1、表2所示.

表1 例1中方向为d时数值结果

表2 例1中方向为-d时数值结果
例2 外边界曲线Γ0,内边界曲线Γ1,
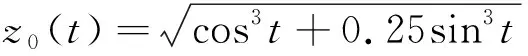
Γ1:z1(t)=(0.6cost,0.2sint),t∈[0,2π].波数为k0=2.5,k1=2.远场模式u∞(d)和u∞(-d)的数值结果如表3,表4所示.

表3 例2中方向为d时数值结果

表4 例2中方向为-d时数值结果
为了验证此方法的可行性,我们取d=(-1,0),λ0=1与文献[10]的结果做了一个对照,数值结果是一致的.同时,例1、例2的数值结果也表明该方法的收敛速度是非常快的,所以文中的方法是可行有效的.
4 结束语
目前,对于混合边界在分层介质中的声波散射问题的数值解暂时还没有有效的解决方式.因此,我们期望本文中所用方法可以有效地解决该类问题.
[1] Wang H B,Liu J J.Numerical solution for the helmholtz equation with mixed boundary condition[J].Numerical Mathematic,2007,16(3):203-214.
[2] 王连堂,杨阿莉,管金友,等.阻尼边界条件散射问题的数值解法[J].数学物理学报,2009,29(6):1 704-1 713.
[3] Monch L.On the numerical solution of the direct scattering problem for an open sound-hard arc[J].Computational and Applied Mathematics,1996,71:343-356.
[4] Kress R,Lee Kuo-Ming.Integral equation methods for scattering from an impedance crack[J].Computational and Applied Mathematics,2003,161:161-177.
[5] 刘晓东.分层介质中声波与电磁波散射问题及其反问题[D].北京:中国科学院研究生院,2010.
[6] Colton D,Kress R.Inverse acoustic and electromagnetic scattering theory[M].Springer Verlag,2003:38-41.
[7] Colton D,Kress R.Integeral equation methods in scattering theroy[M].New York:WileY-interscience Publication,1983.
[8] Kress R.Linear integeral equations[M].Berlin: Springer Verlag,1998.
[9] Kress R.On the numerical solution of a hypersingular integer equation inscattering theory[J].Computational and Applied Mathematics,1995,61:345-360.
[10] Yaman F.Location and shape reconstructions of sound-soft obstacles buried in penetrable cylinders[J].Inverse Problems,2009,25:1-17.
