民办继续教育培训机构教学质量动态评估方法研究

杨劲松，凌培亮，张 蔷

(同济大学 现代远程教育研究所，上海200092)

培训行业是一个非常诱人的行业，2010年3月出版的《2009—2012年中国教育培训市场调查与发展前景分析报告》中显示，中国培训业规模正以每年30%的速度递增，中国教育培训的潜在市场规模达3000 亿元，并保持着迅猛的发展态势。由于民办继续教育具有专业性强、个性化突出、方式方法灵活等特点，其发展必须直接面向社会、面向求学对象，取得社会的支持。在市场经济条件下，民办培训机构的可营利性往往容易被经营者放大效应，继续教育培训机构成为赚钱的工具，进而降低教育质量。为了防止民办培训机构为降低成本而牺牲教学质量，走向“唯利是图”的歧途，教育行政部门要确定适当的评价教学质量的标准。如果学校及其他教育机构在盈利的时候，没有达到评价教学质量的最低标准，那么就应该接受教育行政机构和有关检查与监督权力部门的处罚或取缔。

由于民办培训机构面向市场的办学特点和环境具有复杂性，项目种类、实施周期甚至社会因素都可能带来评定规则和评定条件的不断变化，民办培训机构教学质量的评定过程必须适应动态评估规则。研究适应规则动态演化具有模糊推理能力的民办培训机构教学质量评定机制，并使评估结果更加规范和科学，是一个有意义的内容。

一、民办培训机构教学质量动态评定机制实现思路

引入自然科学相关范畴的研究方法，建立适应推理规则动态变化并具有模糊评价能力的民办培训机构教学质量评定机制，是解决此项问题的有效途径。问题解决的思路和方向在于引入产生式规则、模糊Petri 网和模糊数学概念，使用产生式规则收集各项教学质量评估项，由此转化成模糊Petri 网表示的教学质量评定规则体系，以实现能适应民办培训机构教学质量评估规则动态变化并具有模糊评价能力的教学质量评定机制及计算方法。具体操作办法如下:

1．使用产生式规则表达民办培训机构教学质量的评估项。从心理学角度分析，人类在作出判断行为时的主要手段是因果关系推理，这种推理方式最直观的表达方式即产生式规则。由于这种知识表达方式接近人类思维以及交流的方式，因而得以应用在各种不同的领域，也是目前应用最广泛的知识表示手段之一。正是由于产生式规则对知识表示直观简明的优点，它符合人类的推理习惯的特点，也更利于民办培训机构教学质量的各评估项的收集。

2．将孤立的产生式规则统一成完整的模糊Petri 网表示的教学质量评定网络。这将形成一张包含民办培训机构教学质量评估特征项的评估体系集，是所有特定项目教学质量评估指标体系的父集。单一的教学质量评估项很难清晰地刻画评估体系的整体情况。模糊Petri 网的优点在于结合了Petri 网的图形描述能力，使得教学质量评估项的表示简单、清晰，又能表现出教学质量评估体系中的结构化特性。同时，由于Petri 网理论建立在较为严密的数学基础上，用Petri 网表示的产生式规则库内部逻辑为更加清晰，推力规则更数学形式化，便于知识的分析、推理、测试以及决策支持等。

3．使用基于模糊Petri 网的逆向知识推理方法提炼适用于民办培训机构教学质量具体项目的个性化评估体系，它将是第二步形成的完整评估体系集的子集，能更有效地刻画和表达特定民办培训机构项目，使评估更具针对性、科学性。

4．利用模糊Petri 网及模糊数学计算规则，根据基础数据条件计算民办培训机构教学质量等级。在这里还可以开展更进一步的研究，但由于研究中教学质量评估体系的模糊规则置信度的确定很大程度上依赖专家的经验，所以难以精确获得。因此，需进一步研究教学质量评估体系置信度的优化方法，将人工智能领域的算法引入模糊规则置信度的寻优过程，以有效提高教学质量评估体系的泛化能力，降低教学质量评估体系的实际应用难度。

5．由此建立的评估机制可以动态更新，按照市场条件或环境变化，只需更改或调整产生式规则，系统可自动调整模糊Petri 网表示的教学质量评定体系，以支持动态评估机制。

二、由孤立的产生式规则形成模糊Petri 网表示的教学质量评定规则体系

此过程的重心在于如何将孤立的产生式规则转化为模糊Petri 网表示的教学质量评定规则体系。

客观世界中存在着大量因果关系，产生式适合于表达这种因果关系。产生式规则的含义是:如果前提条件P 满足，则可推出Q 成立或执行Q 操作。产生式的基本形式为式(1．1)、式(1．2):

或则

其中，P 是产生式的前提条件，用于指明何种情况下该条件成立，Q 是一组结论或操作，用于指明前提条件成立时应执行的操作。

定义1 令R 是模糊产生式规则集，R={R1，R2，…Rn}。对于其中每个规则，Ri的定义为IF diAND djTHEN dk(CF=μi)。其中，di、dj和dk为命题，它们的真值是介于0 和1 之间的实数;di、dj被称为条件谓词，dk为结论谓词;Ri的条件谓词集合记为FP(Ri)，Ri的结论谓词集合记为CP(Ri);μi为规则的模糊因子置信度CF，μi∈［0，1］。μi越接近1，规则Ri越可信。

定义2 按表示模糊产生式规则的FPN 模型来表示一个基于规则的系统。根据文献［1］的定义，一个FPN 被定义为八元组:

FPN=(P，T，D，I，O，f，α，β)

这里:P={p1，p2，…，pn}是一个有限库所集合;

T={t1，t2，…，tm}是一个有限变迁集合;

D={d1，d2，…，dn}是一个有限命题集合;

|P|=|D|;

I:T→P∞是一个输入函数，映射一个变迁到它的输入库所集合;

O:T→P∞是一个输出函数，映射一个变迁到它的输出库所集合;

f:T→［0，1］是一个函数，映射变迁到一个从0－1 的数值，用来表示变迁对应的推理规则的置信度(CF);

α:P→［0，1］是一个函数，映射库所到一个从0－1 的数值，用来表示该库所对应的命题成立的真实度;

β:P→D 是一个函数，映射库所对应的命题。

为有利于模糊产生式规则向模糊Petri 网的转换，论文限定模糊式产生规则输入时仅限于以下类型1 和类型2 两种基本形式。

类型1:Ri:IF djTHEN dk(CF=μi)，其中产生式规则Ri的谓词dj，dk用模糊Petri 网的库所pj和pk表示，产生式规则Ri的因果关系用FPN 的变迁ti表示，模糊产生式规则的置信度用ti的置信度表示。Ri的FPN 模型为图1。

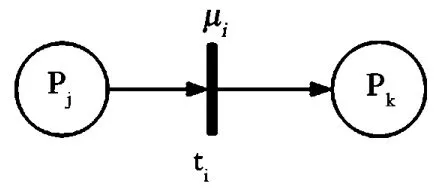
图1 Ri 的FPN 模型

类型2:RjIF dj1AND dj2AND … AND djnTHEN dk(CF=μi)。Rj的FPN 模型为图2。

其他常见的模糊产生式规则还有:

类型3:

Rk:IF djTHEN dk1(CF=μ1)AND dk2(CF=μ2)AND … AND dki(CF=μi)

类型3 可转化为一组类型1 的模糊产生式规则组:

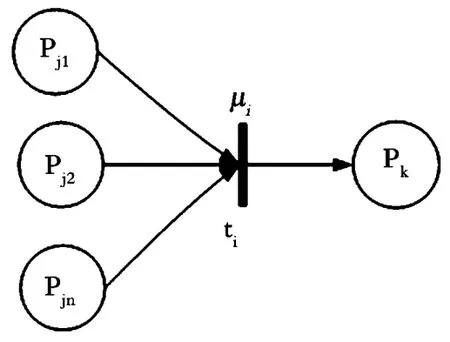
图2 Rj 的FPN 模型

Rk1:IF djTHEN dk1(CF=μ1);Rk2:IF djTHEN dk2(CF=μ2);…;Rki:IF djTHEN dki(CF=μi)

类型4:

Rj:IF dj1OR dj2OR …OR djiTHEN dk(CF=μi)。

类型4 可转化为一组类型1 的模糊产生式规则组:

Rk1:IF dj1THEN dk(CF=μ1);Rk2:IF dj2THEN dk(CF=μ2);…;Rki:IF djiTHEN dk(CF=μi)

类型5:

Rk:IF djTHEN dk1(CF=μ1)OR dk2(CF=μ2)OR …OR dki(CF=μi)

由于这种类型的模糊产生式规则无特定的结论产生，无法演绎推理，在实际应用中不允许出现。

当模糊产生式规则向FPN 迁移时，FPN 的库表示模糊产生式规则的命题;FPN 的变迁表示命题之间的因果关系;FPN 的托肯值代表模糊产生式规则的命题的真实度;FPN 的每个变迁有一个置信度表示每一个模糊产生式规则的置信度。

假设有模糊产生式规则库R={R1，R2，…Rn}，其中Ri均为转换成类型1 和类型2 两种基本形式的模糊产生式规则;R 中所有谓词集为D={d1，d2，…di}，谓词在D 中不重复出现;P、T 为FPN 的模糊库所集和模糊变迁集，将R 转换为FPN 的算法如下:

(1)i=1，T=φ，P=D;

(2)新建变迁ti，另CFi=μi;

(3)在FPN 中增加表示规则Ri条件谓词集合的库所集到变迁ti输入弧，在FPN 中增加变迁ti到表示规则Ri结论谓词集合的库所集输出弧;

(4)如果i=n，转换完成;否则，i=i+1，转(2)。

在此规则下，使用产生式规则表达高校继续教育合作办学的各项教学质量评估项即可转化成模糊Petri 网表示的教学质量评定规则体系。如适用环境或部分评估规则调整，系统可动态调整整个评估体系。

三、结束语

研究适应规则动态演化具有模糊推理能力的民办培训机构教学质量评定机制，能使教学质量评估结果更有项目针对性和科学性。论文使用产生式规则收集各项教学质量评估项，由此转化成模糊Petri 网表示的教学质量评定规则体系，提供了一种民办培训机构教学质量评估动态评估体系的解决思路和操作办法。

［1］ CHEN Shyi－Ming，Ke Jyh－Sheng，Chang Jin－Fu．Knowledge representation using fuzzy Petri nets［J］．IEEE Transaction on Knowledge and Data Engineering，1990，2(3)．

［2］ 李尘．服务质量对民办培训机构品牌忠诚的影响——以广州民办培训机构为例［J］．中国经贸导刊，2010，(1):52．

［3］ CHEN Shyi－Ming，Ke Jyh－Sheng，Chang Jin－Fu．Knowledge representation using fuzzy Petri nets［J］．IEEE Transaction on Knowledge and Data Engineering．1990，2(3):311－31．

［4］ 门鹏，段振华．基于代数的模糊Petri 网逆向推理算法［J］．系统仿真学报，2007，(S1):165－167．

［5］ 马金强．我国民办职业教育的发展、问题、机遇及对策［J］．职教论坛，2007，(9):40－43．

［6］ 周适，顾昕．中国职业教育改革与发展中的政府与市场［J］．东岳论丛．2011，(2):127－132．