上游粗糙元对叶片根部马蹄涡的影响

王建明，祝 魁，王虎彬，郑耀辉

(沈阳航空航天大学航空航天工程学部(院)，沈阳110136)

角区结构广泛存在于航空飞行器及动力装置中，如飞机上机翼与机体的连接处、发动机压气机或涡轮中的叶片根部等都是典型的角区结构。由于粘性作用与逆压梯度的存在，角区中边界层产生三维分离流动，流场中会出现具有复杂的演化机理的马蹄涡结构［1－3］。因此不管是在理论基础研究中还是在工程实际应用上，研究角区流动都具有较高的学术价值［4］。一般马蹄涡结构会对系统性能产生不利地影响，如引起流动噪音增强、系统结构振动失稳和增加热损失等，为此近些年来许多学者针对如何消弱甚至消除角区马蹄涡强度的流动控制方法进行了大量地研究。研究的载体大多是由简化了的圆柱–平板或叶片–平板所组成。利用叶片上游平板的空腔结构［5］、减小圆柱头部的钝度［6］、在圆柱前附加小圆棒［7］或倾斜棒［8－9］减小压差阻力等方法都可以减弱圆柱前马蹄涡结构;而利用文氏管引射叶片根部的流体［10］、叶形后掠［11］、叶片前增加类似三角翼的结构［12］或整流片［13］等方法亦能够达到消弱叶片根部马蹄涡结构的目的。同样本文为方便研究叶片根部的马蹄涡结构及其控制方法，继续沿用由(前端是长短轴比为3:2的椭圆接NACA0020翼型尾部构成［14］)Rood翼型所组成的叶片–平板结构作为研究载体。

1 计算模型

图1所示为叶片－平板结构，相应的计算域尺寸与网格见图2。来流速度Uref方向沿X轴从左至右，在X轴两侧对称地布置Rood翼型叶片，翼型前缘顶点位于坐标原点处，叶片高为0.2m，弦长为0.255m，厚度T=0.06m。在叶片上游距离前缘位置 d处放置两排由高为 h、边长为0.02m的小方块所组成的粗糙元;两排粗糙元之间相互错开且间距为0.02m(图1(b))。本文通过改变粗糙元的位置d和高度h两个参数来实现不同的控制工况，其中d分别取d/T=2/3、d/T=1、d/T=4/3，h 分别取 h/T=1/30、h/T=1/20、h/T=1/15、h/T=1/12。

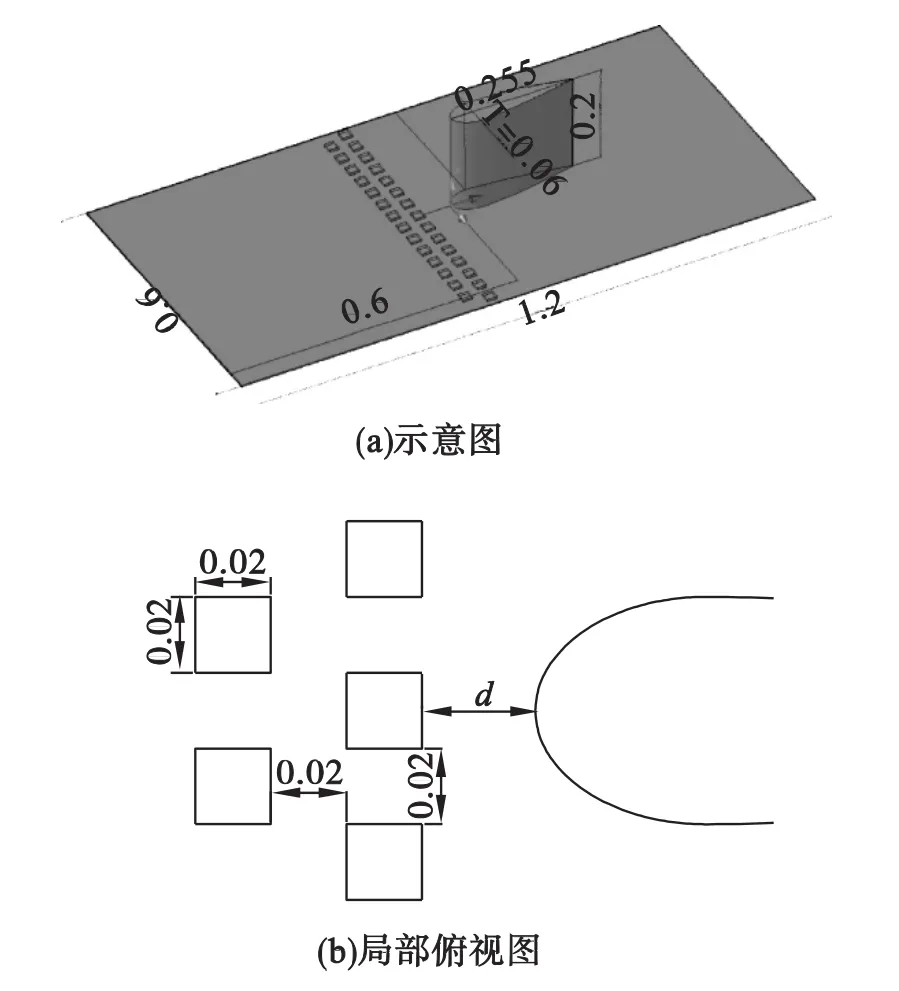
图1 模型尺寸(单位:米)

图2为计算域网格的划分情况，靠近壁面处采用边界层网格，第一层网格高设为0.1mm，沿高度网格增长率设为1.1倍，总网格数为200万左右。计算时选用剪切应力输运(SST k-ω)湍流模型，该模型适用范围广，可以用于带逆压梯度的流动计算与翼型扰流计算等。采用压力基隐式求解器，速度和压力的耦合采用SIMPLE算法，各参数离散采用二阶迎风格式。设入口速度为30m/s，出口采用压力出口。马蹄涡涡心的坐标用Xv和Yv表示，定义涡量系数，表面摩擦系数，其中Ω是涡量，T是叶片厚度，τw是壁面剪切应力。

图2 计算域与网格

2 结果与分析

2.1 计算结果验证

以入口速度Uref=30m/s为参数，计算当叶片厚度T是特征尺度时的雷诺数为1.2×105，并且当叶片中心距平板前缘的长度是特征尺度时的雷诺数为1.35×106，由文献［14］可判断出叶片根部流动状态是湍流形式的。对于不加粗糙元的基本流态来说，其叶片前对称面内(Z/T=0)的速度矢量与流线分布如图3所示，其中VM表示了流动速度矢量大小，相应的流动结构与文献［15］所提到的相一致。

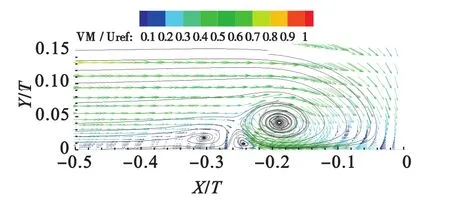
图3 Z/T=0平面内基本流态速度矢量和流线图

为证明计算结果的可信性，参考文献［14］的实验结果与本文计算结果的对比情况如图4所示。选用的是叶片上游对称面内(Z/T=0)不同位置的流向速度U/Uref的结果进行比较。可以看出数值模拟与实验结果虽有一定的差别，但大体上还是比较吻合的，在回流区的大尺度流动结构上的曲线趋势是基本一致的，说明本文所绘制的网格和所选的湍流模型具有一定的参考价值，后续的计算结果是比较可靠的。

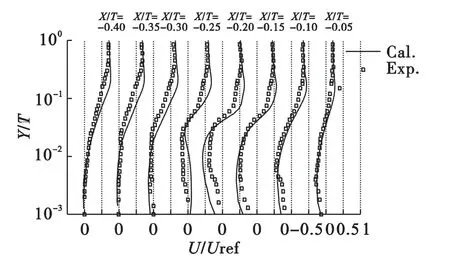
图4 Z/T=0平面内基本流态U/Uref的计算数据与实验数据［14］对比

2.2 粗糙元位置的影响

与速度矢量相比，涡量更容易显示出马蹄涡的空间分布，图5(a)是h/T=1/20粗糙元处于不同位置时叶片上游对称面内(Z/T=0)的涡量分布图，在叶片上游增加粗糙元，在粗糙元之间和顶部产生纵向涡和横向涡的漩涡结构，对流场的扰动增加，因此有效地改变了漩涡的空间尺度与马蹄涡的涡心涡量。基本流态时的主马蹄涡涡心处Cv=－38(图5(a－1));粗糙元位置d/T=2/3时Cv=－22;d/T=1时Cv=－14;d/T=4/3时Cv=－30。由此可以看出三种控制工况下，主马蹄涡涡心涡量较基本流态都有所降低(图5(a－2)－图5(a－4))，特别是d/T=1时控制效果最好。利用壁面剪切力系数Cf能够很好的衡量马蹄涡的强度，它综合了马蹄涡涡量分布与空间尺度的作用［10］。其中d/T=2/3与d/T=4/3时Cf值与基本流态相差不多，相比之下当d/T=1时对应的Cf值减小了许多(表1)，由此可见当粗糙元布置在距翼型前缘较近的d/T=2/3处和较远的d/T=4/3处控制效果都不是最佳，而当布置在d/T=1附近时，主马蹄涡强度会被有效地削弱，d/T=1是较佳的控制参数。

在平面X/T=3/4内讨论了粗糙元对于流向马蹄涡的影响(图5(b))。由于空气来流通过上游粗糙元时产生的流动结构影响到了下游的流场，相比基本流态时流动控制下的流向涡范围变大(图5(b)－图6(b))。其中d/T=1时，相应的Cv=5(图5(b－3))，相当于基本流态的一半左右。相比之下对于另两种工况来说，流向涡控制效果不佳，结合上游对称面内主马蹄涡控制效果来看，进一步说明d/T=1是比较好的控制参数。

图5 粗糙元处于不同位置下叶片根部马蹄涡涡量系数图(h/T=1/20)

2.3 粗糙元高度的影响

本小节讨论在参数d/T=1的基础上不同h/T的粗糙元影响下的流动工况，进一步优化流动控制效果。图6(a)是粗糙元处于不同高度下叶片上游对称面内的涡量分布图。结合前文所示共对粗糙元高度进行了4种工况的调整(图5(a－3)、图6(a))，从图中可以看出随着h/T的增加，扰动的范围明显增大且主马蹄涡有远离叶片根部的趋势。粗糙元高度为h/T=1/30时，涡心位置为(－0.235，0.048)，相应的 Cv= －38;h/T=1/15时，涡心位置为(－0.435，0.061)，Cv= －14;h/T=1/12时，涡心位置为(－0.506，0.066)，Cv=－14。除h/T=1/30外，另3种工况下主马蹄涡涡心涡量都明显减小。涡心下的壁面剪切力系数Cf值也都有所降低，并且存在随着高度的增加而减小的趋势(表1)，说明相对较高的粗糙元对控制效果来说是有利的。其中h/T=1/15和h/T=1/20时的Cf值相差不多;h/T=1/12时，Cf为基本流态的1/2左右。除h/T=1/30外，另外3种工况在X/T=3/4平面内流向涡涡心涡量也都明显下降(图5(b－3)、图6(b))。通过以上分析考虑到既要很好地削弱马蹄涡强度又不过分增强扰动范围，h/T=1/20是较佳的控制参数。而此参数结合图3来看与主马蹄涡涡心高度差不多，说明在选择合适的扰动体来影响马蹄涡时，高度应略大于马蹄涡涡心高度(Yv/T=1/25，表1)为宜。

表1 涡心位置与涡心下的平板表面摩擦系数

图6 粗糙元处于不同高度下叶片根部涡量系数图(d/T=1)

由于角区逆压梯度的作用，边界层三维分离流动产生马蹄涡结构［11］;通过粗糙元的作用，处在上游的粗糙元会产生横向涡与纵向涡并流向下游，会促使沿流向的具有较高动能的流体质点从边界层外被裹入到边界层中，这样会使层内流体质点所具有的平均流向的动量增加;并且这种是连续进行的过程，当供给的能量达到一定程度时，边界层中流体就有了抵御逆压梯度和克服表面摩擦的能力，最终减弱了分离的强度。选择粗糙元的位置及高度控制在一定范围内才能使上述过程更好地进行。

3 结论

在简化了的叶片－平板结构的上游某位置布置一组粗糙元来削弱叶片根部马蹄涡系，采用数值模拟的手段计算涡量分布，得到如下主要结论:

(1)文中涉及到的不同控制工况下的粗糙元都能不同程度地削弱叶片根部马蹄涡结构强度;

(2)布置在距叶片根部d/T=1处且高度h/T=1/20的粗糙元在其后的流动结构与流向涡的空间尺度以及主马蹄涡涡量的综合控制效果较好;并且主马蹄涡强度会降到原来的1/3左右;

(3)通过比较各工况的主马蹄涡涡心下壁面剪切力系数Cf值，都存在随着高度的增加而减小的趋势，说明相对较高的粗糙元对主马蹄涡控制效果来说是有利的，但对叶身两侧的流向涡来说都存在使其远离叶身的趋势。

［1］Baker C J.The oscillation of horseshoe vortex system［J］.J Fluids Eng，1991，113(4):89 －95.

［2］周逊，韩万金.涡轮矩形叶栅中的旋涡模型的进展回顾［J］.航空动力学报，2001，16(3):198 －204.

［3］刘火星，陈矛章，蒋浩康.扩压叶栅角区马蹄涡的实验研究［J］.工程热物理学报，2000，21(6):703－706.

［4］Simpson R L.Junction flows［J］.Annu Rev Fluid Mech，2001，33:415 －43.

［5］Kang K J，Kim T，Song S J.Strengths of horseshoe vortices around a circular cylinder with an upstream cavity［J］.J Mech Sci Technol，2009，23(7):1773 －1778.

［6］Wei Q D，Wang J M，Chen G，et al.Modification of junction flows by altering the section shapes of the cylinders［J］.J Visual-Japan，2008，11(2):115 －124.

［7］Wang J J，Zhang P F，LU S F，et al.Drag reduction of a circular cylinder using an upstream rod［J］.Flow Turbul Combust，2006，76(1):83 －101.

［8］Wang J M，Bi W T，Wei Q D.Effects of an inclined rod on circular cylinder-plate junction flow［J］.Exp Fluids，2009，46(6):1093 －1104.

［9］王建明，刘炜，艾延廷，等.圆柱－平板角区湍流流动控制的风洞试验研究［J］.实验流体力学，2011，25(5):10－15.

［10］王建明，刘炜，徐志晖，等.文氏效应在叶片根部马蹄涡控制中的应用［J］.航空动力学报，2011，11:2617－2622.

［11］张华，吕志咏.后掠翼身交接区流动结构及参数影响研究［J］.流体力学实验与测量，2000，14(2):16－20.

［12］Gupta A K.Hydrodynamic modification of the horseshoe vortex at a vertical pier junction with ground［J］.Phys.Fluids，1987，30(4):1213 －1215.

［13］Devenport W J，Simpson R L，Dewitz M B，et al.Effects of a leading-edge fillet on the flow past an appendagebody junction［J］.AIAA J，1992，30(9):2177 －2183.

［14］Devenport W J，Simpson R L.Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction［J］.J Fluid Mech，1990，210(1):23－55.

［15］Baker C J.The turbulent horseshoe vortex［J］.J Wind Eng Ind AeroD，1980，6(1):9 －23.