基于改进变密度法的飞机垂尾拓扑优化设计研究
2013-01-22邱福生季武强徐厚超
邱福生,季武强,徐厚超
(沈阳航空航天大学辽宁省数字化工艺仿真与测试技术重点实验室,沈阳110136)
按照设计变量的不同,结构拓扑优化可以分为以下3种:尺寸优化、形状优化和拓扑优化[1]。拓扑优化能在给定的约束和边界条件下,通过改变结构布局使结构的设计要求及性能达到最优。与尺寸优化和形状优化相比,拓扑优化的经济效果明显,发展前景广阔,应用范围广泛,在优化中能产生新的构型,是结构实现自动化智能设计广泛采用的设计方法。按照不同的优化对象的性质,拓扑优化可分为离散体拓扑优化和连续体拓扑优化两种方法[2]。连续体拓扑优化与离散体拓扑优化相比,有更加广泛应用范围的同时,也存在模型描述困难,设计变量较多,计算量较大,对载荷的敏感度较强等各种问题。
为了实现飞机的减重目标,本文通过拓扑优化技术实现飞机垂尾减重目标。一直以来连续体拓扑优化技术发展的比较缓慢,直到1988年Bendson等人[3]提出均匀化方法之后,它才得以快速发展。目前比较常用的连续体拓扑优化方法有均匀化方法[3]、变厚度法[4]、变密度法[5]、渐进结构优化方法[6]等。以上各种连续体拓扑优化方法都有各自的优势和擅长处理的问题,但是又都有一定的局限性。
本文主要以变密度法的研究为主,通过引入约束因子的方法改进变密度法实现飞机垂尾的拓扑优化设计;同时与ANSYS拓扑优化模块对垂尾简化模型进行优化设计和结果分析比较,发现带约束因子的变密度法在处理飞机垂尾的拓扑优化问题时,不仅仅可以找到新的构型,同时较ANSYS软件简便、有效。
1 带约束因子变密度法
带约束因子变密度法是在变密度法的基础上引入约束,通过约束因子优越的控制性,使得优化过程中对飞机垂尾多约束的控制更加简便有效,更加符合复杂垂尾结构拓扑优化的实现要求。变密度法是一种已经被证明的并且十分可靠的拓扑优化算法,但是它有一定的局限性:设计变量只包含单元的伪密度(Pseudo-density),难以在优化过程中根据实际设计要求控制多约束情况,例如单元的删除和保留选择、多种位移约束、或者其他更复杂的优化设计要求等;当优化结束后不能直接删除单元,需要根据设计要求人为给定一个伪密度值来删除单元,进而得到最终的结构形式。因此本文通过引入约束因子,对变密度拓扑优化设计法进行改进,使其可以更好地完成飞机垂尾的拓扑优化设计。带有约束因子的伪密度数学模型:
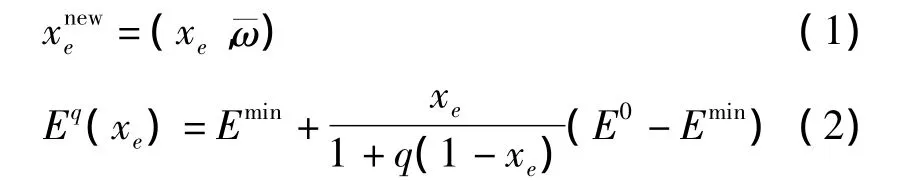
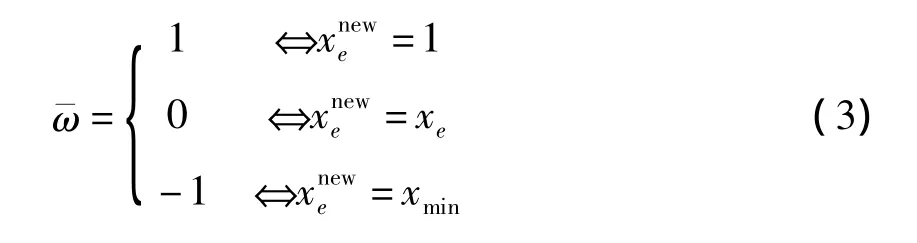
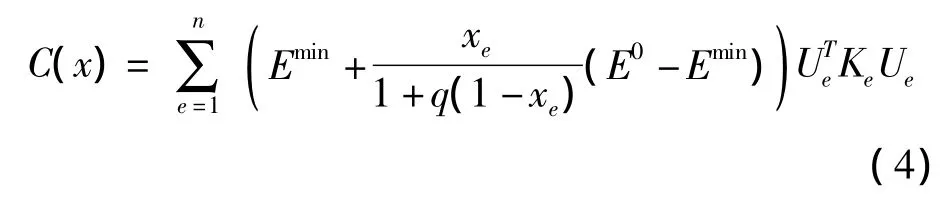
式(4)中:C(x)是拓扑优化的目标函数,表示结构柔度(结构应变能大小),Ue和分别是结构节点位移向量和节点位移向量的转置,用式(1)中的代替式中的伪密度xe。其他的变量参数与式(1)和式(2)中相同。
2 建模
2.1 模型的简化
飞机的垂尾大都是由垂直安定面和方向舵组成的,对垂尾的设计就要充分考虑上述两部分的功能和受载荷情况。以客机为例,客机的飞行状态相对平稳,在模型简化过程中只考虑飞机飞行时受到的气动载荷,并且该载荷只作用在垂尾前缘,因此对客机的飞机垂尾进行模型简化,将气动载荷简化为垂尾前缘结点载荷,垂尾的垂直安定面下端固定在机身上,将三维的垂尾简化成二维的模型来分析,其运算得到的结果也比较符合实际的垂尾情况。
根据拓扑优化设计要求定义飞机垂尾的设计域:按照垂尾的边界条件,将模型的下端从0~4内的所有节点固定,其在x和y方向上均没有位移;对气动载荷简化,在机翼前缘各个节点上加载指向x轴正向的大小为100N。
2.2 模型的建立
2.2.1 ANSYS 模型
ANSYS软件可用来实现拓扑优化的二维单元有plane2和plane82,本文选取plane82为有限元分析单元。尝试使用ANSYS进行飞机构件模型的建立,但是由于成型软件的固定形式,比较难以处理垂尾边框和控制方向舵的控制杆安装等细节问题。将模型的下端从0~4内的所有节点固定,其在x和y方向上均没有位移;对气动载荷简化,在机翼前缘各个节点上加载指向x轴正向的大小为100N;则使用ANSYS简化的飞机垂尾模型如图1所示。
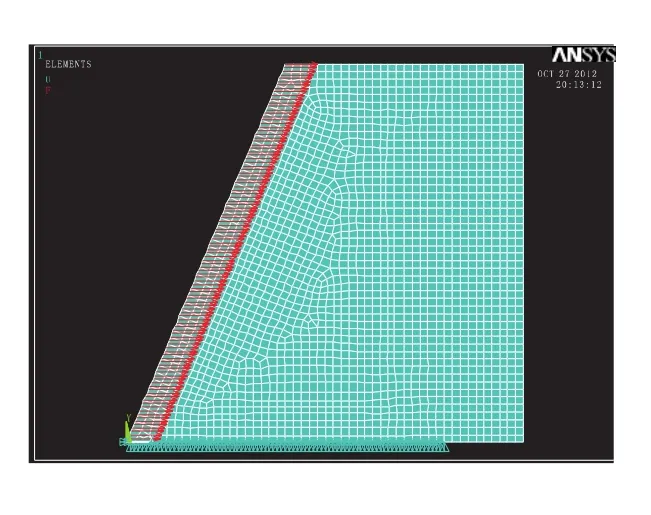
图1 ANSYS建立的飞机垂尾模型
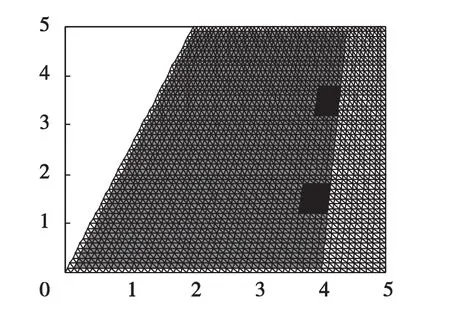
图2 带约束因子变密度法优化模型
2.2.2 约束因子变密度法优化模型
根据飞机垂尾的设计要求简化模型,使用三角形常应变单元划分网格,其单元数量为(2*50*50);定义飞机垂尾的设计域;按照垂尾的边界条件,将模型的下端从0~4内的所有节点固定,其在x和y方向上均没有位移;对气动载荷简化,在机翼前缘各个节点上加载指向x轴正向的大小为100N;考虑到机翼框架的完整性,周围边框处必须保留,而且必须保留安装控制方向舵的控制杆空间(如附录initialization函数)。
在用带约束因子变密度法进行建模时,则可根据具体的设计要求来定义约束因子,这里我们为了简单说明问题,仅仅使用如(2)式的约束因子的定义,保留区的约束因子¯ω=1,例如图2模型中白色部分;删除区的约束因子¯ω=-1,如图2模型中两个黑色方块;优化区的约束因子¯ω=0,如图2模型中的暗灰色部分。而在ANSYS软件建模时我们很难做到边框全部保留的情况,只能通过定义不同的单元编号属性,即只有优化区和非优化区的区别。
3 拓扑优化
3.1 模型拓扑优化结果
根据上面建立的几何优化模型,定义材料及其附加属性,包括弹性模量E=2.5*109GPa,泊松比υ=0.33;同时定义拓扑优化的体积比率因子f=0.5,即仅保留50%的设计域内结构质量。使用ANSYS软件拓扑优化模块进行飞机垂尾的结构拓扑优化,优化结果如图3所示,目标函数变化曲线如图4所示。使用带约束因子变密度法确定的伪密度值(如附录中的 changex函数)的MATLAB程序进行飞机垂尾结构的拓扑优化设计,优化结果如图5所示,目标函数变化曲线如图6所示:

图3 ANSYS拓扑优化结果
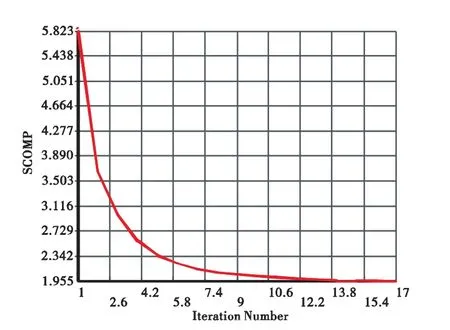
图4 ANSYS拓扑优化目标函数变化曲线

图5 带约束因子变密度法拓扑优化结果
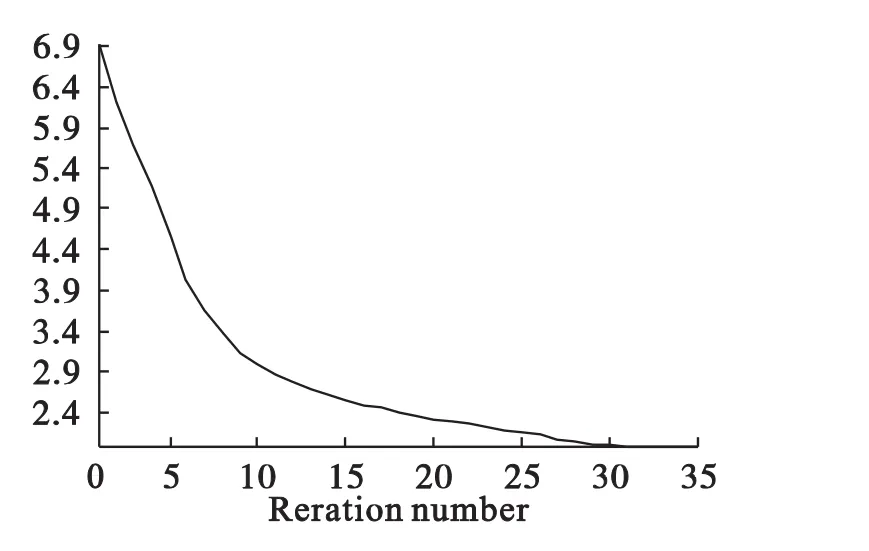
图6 带约束因子变密度法目标函数曲线
3.2 结果分析
从3.1的优化结果中可以看出,ANSYS拓扑优化模块虽然可以处理简单的结构拓扑优化问题,但是对于飞机垂尾的拓扑优化问题,需要考虑到机翼框架的完整性,周围边框处必须保留,而且必须保留安装控制方向舵的控制杆空间等问题时有一定的局限性。但是对于带约束因子变密度法而言则比较容易,只需要对拓扑优化模型的设计变量在初始化过程中根据设计要求定义不同的约束因子(如附录initialization函数),即可轻松、简便、准确的完成垂尾的拓扑优化,如图5所示。
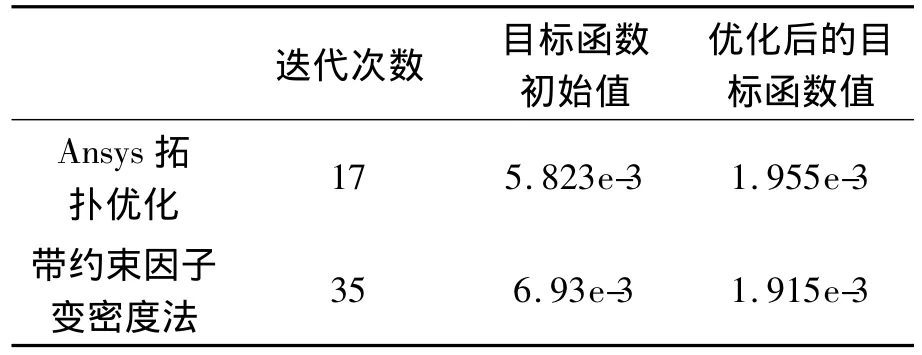
表1 拓扑优化结果
从表1中容易看出,带约束因子变密度法拓扑优化的运算次数较ANSYS软件增加了一倍以上,这是由于一方面使用了约束因子增加设计变量的约束;另一方面因为自己编写的有限元程序相较成熟的ANSYS软件稍有不足之处,进而加大了运算量和迭代次数。但是从目标函数的优化结果来分析,带约束因子变密度法较ANSYS拓扑优化初始的目标函数值稍大,而优化后的结果则相反,带约束因子变密度法的目标函数值比ANSYS的结果更小,这进一步体现了带约束因子变密度法的优越性,越小的目标函数值则说明结果刚度强,因而认为带约束因子变密度法处理垂尾问题时则更加有效、实用、简便。
4 结论
本文通过ANSYS软件的拓扑优化模块和引入带约束因子改进变密度法拓扑优化技术完成简单飞机垂尾模型的拓扑优化设计。通过优化结果可以发现,带约束因子变密度法较ANSYS的拓扑优化模块能够更方便、准确的实现飞机垂尾复杂结构的拓扑优化设计,具有较强的适用性和更加广泛的应用价值,可以尝试将其推广到其他结构设计领域。
附录:部分程序


[1]王伟.机翼结构拓扑优化的一种新渐进结构拓扑优化方法[J].飞机设计,2007,27(4):17 -20.
[2]夏天翔,姚卫星.连续体机构拓扑优化方法评述[J].航空工程进展,2011,2(1):1 -11.
[3]Bendsoe M P,Kikuchi N.Generating optimal topologies in structural design using a homogenization method[J].Computer Methods,1988,71:197 -224.
[4]周克民,胡云昌.利用边厚度单元进行平面连续体的拓扑优化[J].天津城市建设学院学报,2001,7(1):33-35.
[5]Mlejnek H P,R Schirrmacher.An engineer`s approach to optimal material distribution and shape finding computer method in applied mechanic and engineering[J].Computer Methods in Applied Mechanics and Engineering,1993,106(1 -2):1 -26.
[6]Xie Y M,Steven G P.A simple evolutionary procedure for structural optimization[J].Computers and Structures,1993,106(1 -2):1 -26.
[7]Rozvany G I N,Kirsch U,Bendsoe M P,et al.Layout optimization of structures[J].Apply Mech Rev,1995,48:41-119.
[8]M Stolpe,K Svanberg.An alternative interpolation scheme for minimum compliance topology optimization[J].Structural and Multidisciplinary Optimization,2001,22(2):116 -124.
