激光壁面加载模型中相似准则的应用

2013-01-22徐让书严向峰

沈阳航空航天大学学报 2013年1期

徐让书，严向峰

(沈阳航空航天大学航空航天工程学部(院)，沈阳110136)

在前人对激光壁面加载计算模型的研究中，陈发良等［1］利用量纲理论分析了与结构热力响应相关物理量的简单几何相似性。丁升等［2］利用量纲理论分析激光辐照热力耦合基本方程组，得到了激光辐照热力耦合问题的一般性相似准则，且该相似准则不受与材料相关物性参数的约束。而在针对两相流流动的相似计算中，周士昌［3］总结出了一套水平管道中两相流流动(液/固)的相似准则体系。上述研究均证实了相似准则在激光壁面加载模型中的适用性，但在其计算中均不涉及壁面受热熔化后的过程。在壁面材料熔化后所产生的多项流流动中，普通几何缩比模型暴露出流动计算时间尺度与传热计算时间尺度差距过大的问题，影响计算效率。本文利用量纲理论分析多项流流动，再结合两相间作用的定性分析，建立起一套多相流对流换热的相似准则用于优化计算。

1 相似准则理论

为了从模型流动上预测出原型流动的结果，就必须使两者在流动传热现象上相似。即两个互为相似流动的对应位置上的对应物理量都有一定的比例关系。具体来说，两相似流动应满足几何相似、运动相似、动力相似以及初始条件与边界条件的相似。

使用量纲理论分析单一相可压缩粘性流体的一般控制方程组可得:

其中，ρ、p、μ、cp、T 与 k 分别表示密度、压力、动力粘度、定压比热容、温度与热导率;为速度矢量;t为时间;Φ为黏性耗散函数，表征黏性应力做功耗散的能量，其表达式见参考文献［4］。使用方程分析法处理上述控制方程可得:Fr=Fr'，Eu=Eu'，Re=Re'，Ma=Ma'。

由于模型相似化处理主要应用于壁面受热熔化产生两相流阶段，在热量随质量发生迁移的情况下，仅针对单一独立相流动的能量方程也无法准确描述模型中的温度场。为了能够使用方程分析法解析能量方程，在此对计算模型做出如下必要简化:假设模型运算中两相相界面的变化对计算结果不构成决定性影响，由此可将流动换热过程简化为两相流体的内部换热与两相间的对流换热，再考虑到影响相界面稳定的因素，得到如下结果(不再赘述简化推导过程，详见参考资料［5－7］):Pe=Pe'，We=We'。最后，结合 Fluent非稳态计算的特点，表征传热过程不稳定程度的Fo数也应该是相似模型遵循的准则之一。

综上所述，得以构建出一套完整的多相流对流换热的相似准则体系。若要使得简化后的计算模型保持与原型相似的流动传热现象，则相似模型中流体欧拉数Eu、雷诺数Re、马赫数Ma、普朗特数Pr、弗劳德数Fr、韦伯数We、傅立叶数 Fo、流场边界条件及初始条件应与原始模型相同。

2 计算模型

本文中所采用的计算模型如图1所示:

图1 模型尺寸参数

表1 模型尺寸参数

模型中，激光辐照能量定向、静止加载于靶材表面，辐照光斑半径为5mm，辐照能量符合高斯分布，其辐照中心点最高功率为0.8kW/cm2。在模型初始化阶段，假使沿气流方向总长为100mm的钢铁壁面因激光能量加载已存在最大深度为10mm的熔池，温度1673K的熔融钢液填充于图1的凹坑中。常温空气经由入口进入流场，与熔融金属构成两相流流动。

由于计算模型中不存在负压与气蚀，因此在相似准则中无需考虑欧拉数Eu。而在推导得出的相似准则体系中，雷诺数Re，马赫Ma与弗劳德数Fr无法同时满足［8］，结合本文以降低流场速度来调整迭代计算特征时间的目的，在保持模型几何尺寸不变、两相流流动中的Fu悬浮损失准数、Tu推移损失准数、λ沿程损失系数与ζ局部损失系数等相似准则数均相同、改变气流速度的前提下，保证 Re、Pr、Fr、We、Fo5 个相似准则数不变即可。

按上述约束条件得到变换后的相似模型。模型参数如表2所示。

表2 模型计算参数

表2中，模型1参数来源于为原始模型(1∶1)，而模型2参数则源自将风速降低1倍后，按相似准则体系处理后得到的1∶2模型。ρl为熔融金属密度，ρg为空气密度，σ为表面张力系数，τ为计算时间步长。其余边界条件有压力出口pout=1.0125×105pa，系统内无内热源，壁面绝热。两个模型中与传热相关的物性参数保持一致，以保证传热过程不受影响。

使用Fluent软件对原始模型与相似模型进行总时长1.6×10－2s后的非稳态计算后得到原始模型(1∶1)与相似模型(1∶2)的两相流流场分布，如图2、图3所示。

图2 原始模型两相分布(1∶1)

图3 相似模型两相分布(1∶2)

由于激光壁面加载过程中，相界面形状的变化及气流导致的对流换热对能量加载至壁面的传热过程影响较小，而金属流体对于其覆盖壁面区域的保护效应对壁面加载特性的影响更为直接。将模型相似化处理、降低风速以增大计算特征时间尺度的同时，保证靶材熔池中的熔融金属在减速后的附面层气流作用下，其运动规律仍然与实际模型相符。这一点对于附面层影响下激光壁面加载机理的影响远远大于气流减速后对流换热量降低所带来的影响。因此我们更加关注金属流体在附面层气流作用下在传热时间尺度(10－2s量级)内的推移过程。由图2、图3可知，两个模型的相界面沿气流流动方向的推移情况几乎一致，模拟效果良好。而模型1实际计算时长10412s，模型2实际计算时长5981s，相似模拟后的模型缩短计算时间约42.6%，显著提升计算效率。

3 模型适应性分析

模型进行相似化处理后，在实际计算中不可避免会产生误差。由图2、图3即可发现，两相相界面形状在计算过程中存在显著区别。误差产生的根本原因在于方程分析法仅适用于已知描述该流动的基本方程及其全部定解条件的流动现象，因此在涉及复杂的两相流动时显得力不从心。建立图4模型，在50mm×50mm的流场区中存在半径为5mm的液滴，为能够更加明显地观测模型相似处理对两相流流动的影响，特意设置液滴突出于壁面。

在相似化过程中，重力被改变以保证自由相界面在重力作用下的运动过程相同，但沿重力方向流体的加速度则不可能保持一致。此外，相界面的变形及破碎受到流体粘度影响较大。因此，在相似准则适应性验证过程中，需要考虑到重力是否主导流动，以及流体本身的粘度对流动的影响。根据上述要求建立四组对比模型，在接下来的图表中，S表征液滴为熔融钢铁流体，W表征液滴为常温液态水，字母后的数字表征流场进口气流速度(m/s)，相似化处理方式与表2相同。

图4 模型尺寸参数

在低风速、重力主导流动的W1/0.5和S1/0.5两组对比模型中，液滴在重力影响下的运动过程在相似模型中产生了巨大的误差，相似准则体系在此类模型中并不适用。

在高风速、非重力主导流动的 W20/10和S20/10/5/2.5两组对比模型中，以液滴中心随时间的偏移距离及全部液体脱离计算域的时间来考察相似模拟的准确性，得到图5。

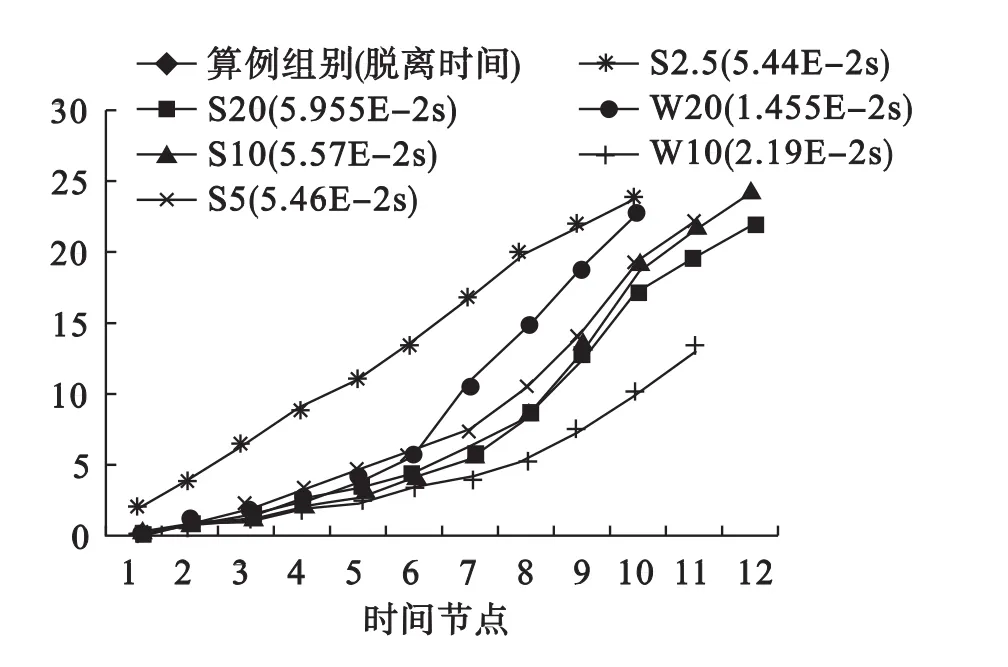
图5 液滴偏移量

对于低粘度流体，W20/10模型中液滴随气流方向的推移速度与自身形变都存在显著差异，液滴脱离计算域时间误差约51%，在此不再赘述。而高粘度流体在相似化处理中体现出了良好的适应性，除S2.5模型外，其余3组模型中液滴沿气流流向上的推移过程模拟得到了几乎相同的结果。在S20/10两模型中，液滴脱离计算域时间误差仅为6.5%。综上可知，本文建立的多相流对流换热的相似准则在两相间存在一相高粘度流体，且重力对流动过程影响较低的情况下，相似变换后的模型计算出的结果与原始模型相符，适用于激光壁面加载模型。