利用矩阵束算法提取水力机组参数的振荡特性
2013-01-22曾保安张立翔昆明理工大学建筑工程学院工程力学系昆明650500
曾保安,曾 云;张立翔(昆明理工大学建筑工程学院工程力学系,昆明 650500)
前言
水力发电机组的稳定性是衡量机组性能的指标之一,机组的稳定性将关系到整个电站及其水工厂房的安全性、国民经济利益和整个电力系 统能否安全运行。因此,机组稳定性受到学者们广泛关注,而表征稳定性的参数分别是振动、摆度和压力脉动,其中振动是机组稳定运行最重要的指标。
水力发电机组的振动按其形式可分为水力振动、机械振动和电磁振动。这三种振动耦合作用于水力机组,以致造成水力机组振动机理很复杂。虽然国内外很多研究者对其做出了巨大的努力,但对其振动机理的理论研究仍然欠缺。一些研究者试图从振动信号中提取机组的振荡信息,找出诱发机组振荡的诱因,以便达到改善机组稳定性的效果。目前对振动信号的提取方法有傅里叶变换法、短时傅里叶变换法、HHT变换法、小波分析法、prony算法、矩阵束算法等。其中傅里叶变换法不能反应振荡的阻尼特性和瞬时频率;HHT变换法会出现模态混叠的现象;小波分析方法是目前信号分析比较完备的方法,但是存在波基选取困难的局限;文献[1]、[2]用prony方法对电力系统暂态或者大规模系统干扰进行稳定性研究,发现该方法对噪音很敏感,抗噪能力很差。文献[3]、[4]提出一种简化分析的方法,不依赖于对象模型可应用于从现场实测数据提取机组参数振荡特性,可对机组任一参数的振荡特性及其影响因素进行详细的分析。文献[5]、[6]研究的是矩阵束算法,此种方法最关键的步骤在于极点求解时进行了去噪处理,采用奇异值分解(SVD)和降低秩的方法把数据中隐含的噪音过滤掉,以免噪音产生虚假极点,其抗噪能力有很大提高。文献[8~12]将几种不同形式的矩阵束算法做了计算精度和计算复杂程度的比较性研究。验证了矩阵束算法具有极强的抗噪能力和广泛使用性。
基于以上的研究结果,本文将矩阵束算法做了一些改进,并用改进的矩阵束算法提取同一工况下水力发电机组角速度、功角、有功、进口处水头、流量和水轮机出力等主要参数的模态信息,进而建立运动模型,初始工况、扰动强度和扰动方向是参数振荡特性的主要影响因素,本文将对这些主要因素如何定量影响振幅、频率和衰减因子的变化进行全面分析,总结出模态信息之间存在的耦联关系,这些研究和探讨为控制和设计提供依据。
1 矩阵束算法
1.1 矩阵束基本算法
(1)模态数的确定。通过采样数据y(1),y(2),…,y(N)构造一个(N-L+1)×L阶 Hankel矩阵:

通过奇异值分解,Y=UΣVT,其中σi是其对角矩阵Σ对角线上的第i个奇异值。由于现场实测数据和模型存在噪声,会产生虚假极点。可用归一化奇异值(σi/σmax)≥β(β为阈值)来辨识出真实极点与虚假极点。把发生突变的归一化奇异值作为初始阈值,逐渐增大或者减小阈值,选取信噪比达到最大时所对应的最大下标i作为最大模态数M,那么前M个极点为真实极点,其对应的归一化奇异值作为阈值。
(2)构造2个Hankel矩阵。由左奇异矩阵V的前M个主奇异向量构成滤噪矩阵V′=[v1,v2,…,vM],构造出两个Hankel矩阵:

其中,V1、V2分别是V′删掉第一行、最后一行而得到;Σ′的前M个奇异值与Σ相同,其余的均为0;
(3)极点与留数的求解。通过对矩阵束Y1和Y2定义,得到以下关系:

由(3)可知,当 λ≠zi时,对角阵Z0-λI的第i行不为零,即Y2-λY1的秩为M,当 λ=zi时,Z0-λI的第i行等于0;矩阵Y2-λY1的秩降为M-1,由相关理论得出,极点zi为矩阵束{Y2,Y1}的广义特征值;即:

其中,Y1+是Y1的伪逆矩阵。
留数的求解可通过最小二乘法计算:

极点与留数求解完毕,利用(10)式求解振幅Ai、相位θi、频率fi和衰减因子αi。
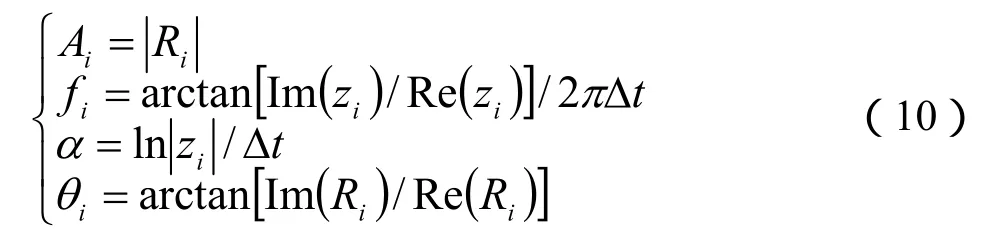
逼近函数为:
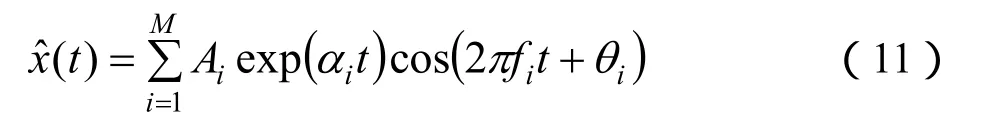
(4)拟合精度的衡量。拟合曲线与原始数据曲线之间的重合度用信噪比(SNR)来衡量;真实数据为y(i),逼近数据为x(i)。

一般认为SNR大于20就是一种可以接受的逼近结果,该值越大,逼近效果越好。
1.2 算法改进
(1)重构数据。式(9)右边的数据y(1),y(2),…,y(n)应使用消噪后的模型数据y′(1),y′(2),…,y′(n),通过式子Y′=UΣ′VT求出矩阵Y′,把Y′反对角线上的数据取平均值作为模型数据。
(2)目前矩阵束算法所研究的振荡模型通常是某个量围绕平衡点的振荡,其相应的相位角只分布在一、四象限,可用(10)式直接求出。但本文研究的振荡模型属于阶跃式的振荡,其相位角应根据留数的实部与虚部对应分布到四个象限上。
(3)影响矩阵束算法精度的因素
1)数据长度至少应取到包含全部振荡信息。
2)采样频率保证大于2fmax,fmax是低频率振荡的最大频率。
3)阈值是消除噪音合理与否的关键;一般选取突变的归一化奇异值作为初始阈值,逐渐增大或者减小,信噪比最大时所对应的归一化奇异值作为阈值。
4)Hankel矩阵列数L也会影响矩阵束算法的精度,一般取L/3-L/2。
2 水力机组模型
2.1 水力系统模型
水力系统采用一管多机的形式,如图1所示,机组2和机组3假设为稳定运行状态。钢管与支管可用等效管i等效。
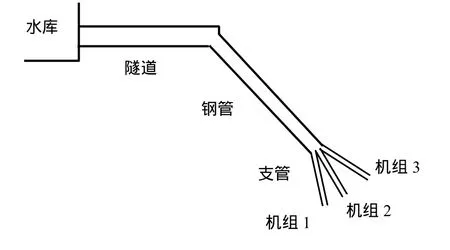
图1 水力系统模型

其中,x=[x1x2x3x4x5],x4=q为流量,x5=y为导叶开度。
水力系统数学模型:

fp(i)为第i路支管与钢管的等效管道损失系数,Z(i)为第i路支管与钢管的等效管道涌浪阻抗,T(i)为第i路支管与钢管的等效管道弹性时间,y为主接力器位移,fpT为隧道水头损失系数,TwT为隧道水流惯性时间系数,Ty为主接力器时间常数,qi为i路支管机组的流量,qj为除第i路支管外机组的流量。
2.2 水轮机力矩计算模型
水轮机力矩模型:

式中,mt为水轮机力矩,At为水轮机增益系数,qnl为水轮机空载流量,ht为水轮机进口处的水头,q为水轮机流量。
2.3 发电机模型
发电机采用单机无穷大三阶实用模型:
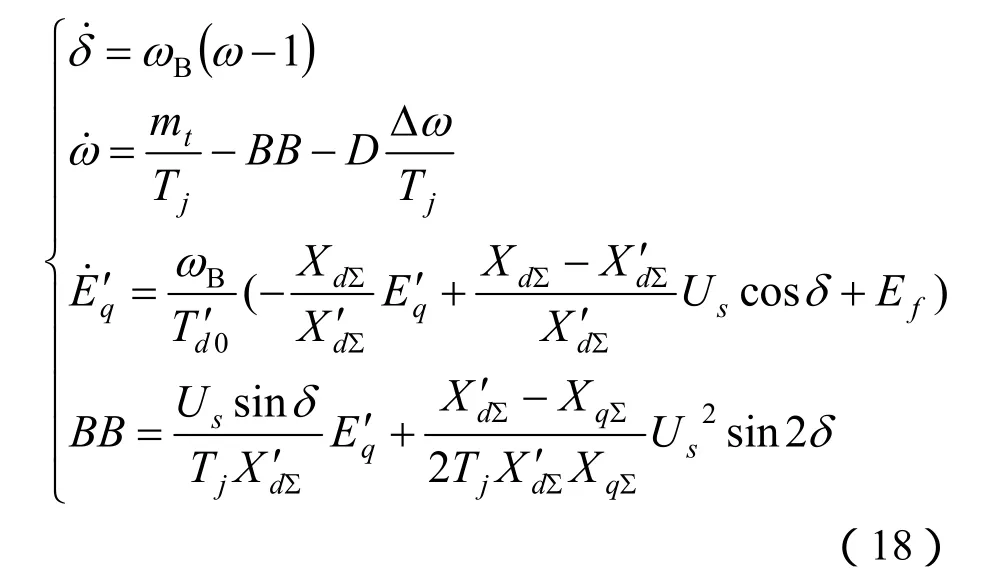
mt为输入机械力矩;Ef为励磁电动势;Td′0为d轴开路暂态时间常数;Tj为机组惯性时间常数ωB=314rad/s为角速度基值;ω为机组角速度;Δω=ω-1;δ为功角;Us为无穷大系统电压;XdΣ=Xd+XT+XL;Xd为d轴电抗;XT为变压器电抗;XL为线路等效电抗;XqΣ=Xq+XT+XL;Xq为q轴电抗;D为阻尼系数;E′q为q轴瞬变电动势;X′dΣ=X′d+XT+XL;X′d为d轴次暂态电抗。
3 模型计算
水力系统模型、发电机模型、水轮机出力模型、典型的并联PID调速器和PI励磁控制器构成完整的水力机组系统进行模型计算。
3.1 发电机功角计算模型
初始工况p=0.5p.u.,目标工况pc=1p.u.,在正常调节时,其建模的计算过程如下:
(1)按频率10Hz进行采样,得到功角的一组仿真数据,并利用这些数据构成一个Hankel矩阵。通过奇异值分解,选取突变的归一化奇异值0.000048作为初始阈值,逐渐增大或减小阈值,以信噪比达到最大时所对应的下标i作为最大模态数M=7,对应的阈值β= 0 .0006。
(2)构造两个Hankel矩阵和求解模型数据。
(3)求出极点与留数。求出的极点有3个实数和2对共轭复数,通过(10)式可知,实数极点对应的频率为0;复数极点以共轭成对形式出现,由特征值分析理论可知,每一对复数极点对应一个振荡模态。
(4)通过(11)式把振荡频率为0与不为0的运动模型分别表示出来。
功角振荡频率为0的运动模型:

功角振荡频率不为0的运动模型:

功角运动模型为δ1(t+δ2)(t)即
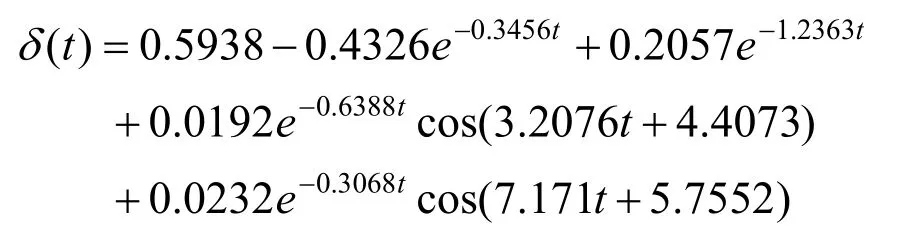
采用上式计算并与仿真数据进行比较,结果如图2所示,功角运动模型曲线δ(t)与仿真曲线基本上完全重合。
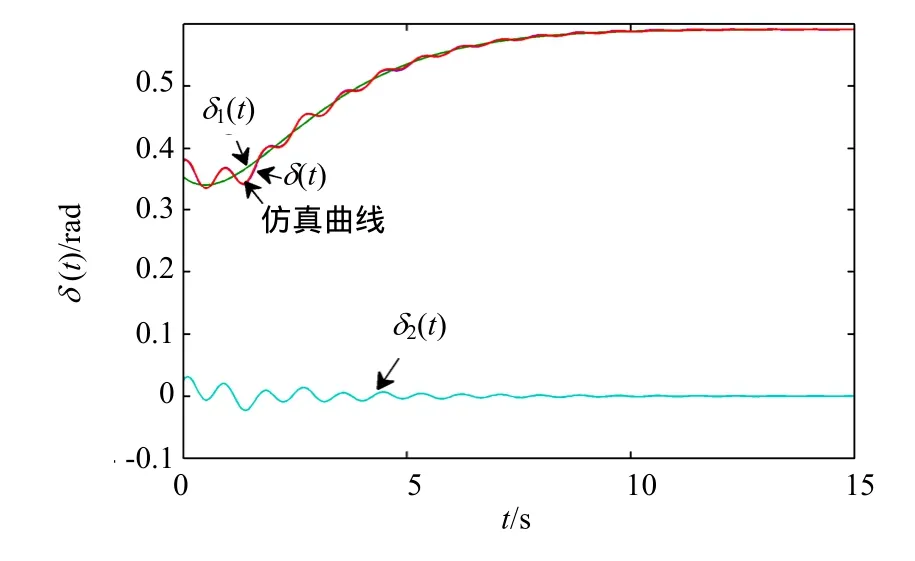
图2 p=0.5p.u., pc=1p.u.时功角的响应曲线
3.2 水轮机出力计算模型
采用与功角相同的工况和计算步骤,提取水轮机出力的运动模型。
水轮机出力振荡频率为0的运动模型:

水轮机出力振荡频率不为0的运动模型:

水轮机出力的运动模型为:

采用上式计算并与仿真数据进行比较,结果如图3所示。水轮机出力运动模型曲线mt(t)与仿真曲线基本上完全重合。

图3 p=0.5p.u., pc=1p.u.时水轮机出力的响应曲线
采用相同的方法研究机组主要参数的运动模型时,发现模态信息之间存在耦联关系,即:
(1)进口处的水头、流量和水轮机出力三个水力参数的振荡频率相近;功角、有功和角速度三个电气参数的振荡频率相近;衰减因子α2相近;各参数的衰减因子r1相近。
(2)水力参数的扰动频率为 0.48Hz左右;电气参数的振动频率为:第一基频0.51Hz左右,第二基频1.1Hz左右;水力参数的频率相近,电气参数的频率相近,说明参数的振荡模态只与参数类型有关。因此,在调节过程中,参数产生振荡是机组结构本身所固有的,其频率为固有频率,其振荡模态为固有振荡模态。
通过采用相同的方法提取各参数的模态信息,并建立运动模型,且与文献[1]建立的运动模型基本一致。因此,可将水力机组参数运动模型归结为两种基本形态:
1)周期衰减运动模型

其中,Ai、αi、fi、θi分别为第i个振荡模态的振幅,衰减因子、频率、相位角。m是周期衰减运动阶数。
2)过阻尼运动模型

xz为运动终值(系统变量的平衡值),Ci、ri分别是第i个过阻尼运动模态的振幅、衰减因子,n是过阻尼运动阶数。
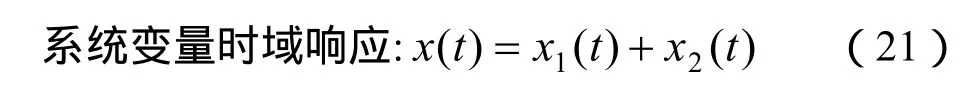
4 模型关联仿真
4.1 初始工况对各参数模态信息的影响
初始工况p对功角、水轮机出力模态信息的影响分别如表1、表2,其中,目标工况pc=1p.u.不变。

表1 初始工况对功角模态信息的影响

表2 初始工况对水轮机出力模态信息的影响
采用相同的方法提取其他各电气参数、水力参数的模态信息随初始工况变化分别与表1、表2中的变化规律一致。即:
(1)各参数的过阻尼运动的阶数、周期衰减运动的阶数不随初始工况而变化,各参数的信噪比随着初始工况减小而减小。
(2)各主要参数的振荡频率受初始工况影响小;电气参数之间的频率是相近的,水力参数之间频率也相近。
(3)各参数的各阶振幅随初始工况减小而增大。
(4)各参数的衰减因子r1和α1随初始工况减小而减小;各参数的衰减因子r2随初始工况减小而增大;电气参数的衰减因子α2随初始工况减小而增大。
4.2 扰动强度对各参数模态信息的影响
初始工况p=0.7p.u.,扰动强度Δp对功角、水轮机出力模态信息的影响分别如表3、表4。

表3 扰动强度对功角模态信息的影响

表4 扰动强度对水轮机出力模态信息的影响
采用相同的方法提取其他各电气参数、水力参数的模态信息随扰动强度的变化分别与表3、表4中的变化规律一致。即:
(1)各参数的过阻尼运动的阶数、周期衰减运动的阶数不随扰动强度而变化,各参数的信噪比随着扰动强度增大而减小。
(2)各参数的振荡频率受扰动强度影响小,电气参数的振荡频率相近,水力参数的振荡频率也相近,且电气参数的振荡频率比水力参数的振荡频率多一阶。
(3)各参数的振幅随扰动强度增大而增大,不受扰动方向的影响。
(4)各参数的衰减因子r1相近;电气参数的衰减因子α2相近;各参数的各阶衰减因子随正向扰动强度增大而减小;各阶衰减因子随负向扰动强度增大而增大。
(5)改变初始工况,Δp与表3、表4一致,可以得出各参数的模态信息随扰动强度的变化不受初始工况影响。
5 结论
(1)改进的MP算法用于提取水力机组各参数模态信息有效性得以验证,体现出良好的抗噪能力;该方法可通过实测数据提取各参数模态信息,不依赖于对象系统模型,因此,可用于电网和机组的在线监测和故障诊断。
(2)通过模态信息建立的两种基本运动形态,能直观、有效地对水力机组的振荡特性进行描述;可通过振动频率推断出诱发振动的诱因。
(3)探讨了各种影响因素下各参数模态信息的变化趋势和耦联关系,为控制设计提供依据。
[1]Hauer J F, Demeure C J, Scharf L L. Initial results in prony analysis of power system response signals [J].IEEE Trans on Power Systems, 1990, 5(1): 80-89.
[2]Grund C E, Paserba J J, J F Hauer. Comparison of prony and eigenanalysis for power system control design[J]. IEEE Transactions on Power Systems,1993,8 (3): 964-971.
[3]曾 云, 张立翔, 王煜. 水轮发电机组振荡特性的简化分析方法[J]. 电机与控制学报, 2009, 13(增刊1): 25-29.
[4]曾云, 沈祖诒, 曹林宁. 低频振荡下发电机响应特性的量化分析[J]. 电力系统及其自动化学报,2008, 20(6): 83-87.
[5]Tapan K.Sarkar , odilon Pereira. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials[J]. IEEE Antennas and Propagation Magazine, 1995, 37(1): 48-55 .
[6]Tapan Kumar Sarkar, Jinhwan Koh. Application of the matrix pencil method for estimating the SEM(Singularity Expansion Method) poles of source-free transient responses from multiple look directions[J]. IEEE Transactions on Antennas and Propagation, 2000, 48(4): 612-618.
[7]Kunder P. 电力系统稳定与控制[M]. 北京:中国电力出版社, 2002.
[8]Muhammad Faisal Khan, Muhammad Tufail.Comparative analysis of various matrix pencil methods for direction of arrival estimation[C].Image Analysis and Signal Processing (IASP),International Conference on,Islamabad,Pakistan,9-11 April 2010.
[9]朱瑞可, 李兴源. 矩阵束算法在同步电机参数辨识中的应用. 电力系统及其自动化学报, 2012, 36(6): 52-56.
[10]François Sarrazin, Ala Sharaiha. Comparison between matrix pencil and prony methods applied on noisy antenna responses[C]. Loug hborough Antennas & Propagation Conference, Loughborough, UK, 14-15 November 2011.
[11]Yanhui Liu, Zaiping Nie. Reducing the number of elements in a linear antenna array by the matrix pencil method[J]. IEEE Transactions on Antennas and Propagation,2008, 56(9):2955-2962.
[12]Nuri Yilmazer, Jinhwan Koh. Utilization of a unitary transform for efficient computation in the matrix pencil method to find the direction of arrival[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(1): 175-181.
