形态梯度解调在电机轴承故障特征提取中的应用研究
2013-01-22李洪儒田海雷
王 冰,李洪儒,田海雷
(石家庄军械工程学院,石家庄 050003)
滚动轴承是电动机构中的关键部件,且极易发生故障,在电机的各种故障中,轴承故障占有相当大的比例,且轴承故障与转子故障极易发生耦合作用,形成复合故障[1]。
电机在正常运转时,当轴承元件表面出现局部损伤类故障后,损伤点与轴承其他元件表面发生接触均会产生冲击作用,从而引起轴承系统固有频率的共振,相应的故障冲击信号会在轴承系统的高频共振信号中调制,表现出非平稳和高频调制的特点。与此同时,在故障发生初期,冲击成分较为微弱,常常被背景噪声或其他轴承故障所淹没,如不平衡、不对中干扰中,难以发现和提取[2]。因此,如何有效地分离故障特征信息,将共振信号中的故障特征解调出来是电机滚动轴承故障提取方法的研究重点。
在轴承故障特征提取中,包络解调方法是一种较为常用的方法。但该方法存在一定的不足,首先包络解调只适用于单一频率调制现象的振动信号。当信号中包含两个及以上加性信号时,其解调结果将会引起误判[3]。其次,包络解调在本质上是通过窄带滤波进行冲击成分的提取,因此,共振频带的选择将直接影响故障识别的效果[4]。
数学形态学(mathematical morphology)是基于随机集论建立起来的一种数学方法,它被广泛地应用于数字图像处理、计算机视觉和模式识别等领域[5],在机械故障信号处理领域,数学形态学也得到了一系列的应用。运用数学形态算子可以有效地提取信号的边缘轮廓以及形态特征,对于滚动轴承损伤故障振动信号,其局部轮廓信息就是轴承故障信号的外包络,因此可以使用数学形态算子来提取冲击信号的边缘轮廓,达到解调的目的[6]。文献[7]基于形态闭运算对分析了轴承故障信号。文献[8-10]运用形态闭运算分析了轴承和齿轮故障信号,取得了较好的解调效果。
本文基于电机轴承故障信号的特点,对比分析了不同形态学运算在信号特征提取方面的特点,重点将数学形态运算与常见的包络解调进行对比,分析得出形态梯度解调具有良好的解调性能。最后,通过对仿真与实例信号的分析表明,形态梯度解调可以有效地提取电机轴承故障信号。
1 数学形态学概述
数学形态学是基于积分几何和随机集的不同于时域、频域分析的非线性方法。其基本思想是用具有一定形态的结构元素去度量和提取信号中的对应形态,以达到对信号进行分析和识别的目的[11]。
1.1 数学形态学基本算子
基本的数学形态算子包括形态腐蚀、形态膨胀、形态开和形态闭算子。其定义如下:
设f(n)和g(n)分别是定义在集合F= { 0,1,...,N-1}和集合G= { 0,1,...,M- 1}上的离散函数,且N≥M。其中,f(n)为原始信号,g(n)为结构元素,f(n)关于g(n)的形态腐蚀和形态膨胀算子分别定义为:
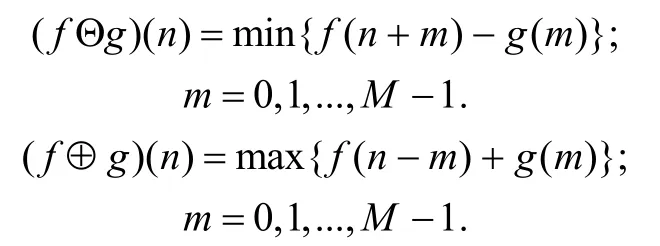
式中:Θ和⊕分别表示形态腐蚀和膨胀运算。
f(n)关于g(n)的形态开与形态闭算子分别定义为:

其中,符号°和·分别表示形态开运算和闭运算。形态开运算是利用结构元素对信号先腐蚀后膨胀;形态闭运算是利用结构元素对信号先膨胀后腐蚀。
1.2 形态梯度运算与形态差值运算
数学形态学中,可以根据实际来选择合适的形态运算,亦可根据需要将四种基本运算进行组合,构建新的形态运算算子。本文重点研究了以下两种:形态梯度算子和形态差值算子。定义如下:
形态梯度算子是信号f(n)通过结构元素g(m)膨胀和腐蚀后的差分,表达式为GRAD(f)=f⊕g(n)-fΘg(n)。形态差值算子是信号分别经过形态闭运算与形态开运算后的差分,表达式如下:DIF(f)=f·g-f°g。
2 仿真分析
数学形态学中的四种基本算子和两种组合算子均可以对信号进行解调并提取特征信息,但效果各不相同。其中,形态膨胀算子可以平滑正向脉冲,抑制负向脉冲;形态腐蚀算子则可以平滑负向脉冲,抑制正向脉冲。形态开运算保留信号的负向脉冲部分,抑制正向脉冲;形态闭运算则保留信号的正向脉冲部分,抑制负向脉冲。相比而言,形态梯度和形态差值算子对信号的正负脉冲均可以进行提取和保留。
在电机轴承振动信号中,信号特征较为复杂,正负向脉冲往往同时存在,而四种基本数学形态算子在解调运算中,脉冲能量损失较大,不利于信号的特征提取,因此,本文重点选取形态梯度和形态差值算子进行分析研究。
2.1 抗双加性低频干扰与解调性能分析
在实际的滚动轴承局部损伤故障中,轴承振动信号是典型的调幅信号,同时,信号中常混杂由转子不平衡、转子不对中故障引起的低频信号干扰。本小节构造了具有双加性低频干扰的实验信号,对比分析了形态梯度算子、形态差值算子、包络解调在处理该类信号时所体现出的抗低频干扰能力与解调效果。
为定量描述解调方法抗双加性低频干扰的能力和解调效果,本文引入低频能量比Q和特征能量比R。
低频能量比Q可以清晰地描述解调方法抗双加性低频干扰的能力,其定义为解调信号在特征频率处能量值与双加性低频信号频率之差处的能量值之比。表达式为:Q=E/C,其中C为双加性信号频率差值处能量值;E为特征频率处能量值。低频能量比越高,说明抗双加性低频干扰的能力越强。
特征能量比R可以定量描述解调方法的解调性能,定义为特征频率前n倍频的局部能量在信号总能量所占的比值,其表达式为:R=(E1+E2+…+En)E,式中,En为解调后的信号频谱在n倍频处的能量值,本文中n取3。R为越大,说明解调效果越好。
采用如下仿真信号进行实验分析,表达式为:y=x1(t)+x2(t)+x3(t)+x4(t)。其中x1(t)为周期性指数衰减冲击信号,用于模拟电机滚动轴承单故障点振动故障,冲击频率为60Hz,周期内冲击函数为2e-300tsin(2π900t);x(t)是均值为0,噪声强度为0.52的高斯白噪声,用来模拟实验环境带来的干扰。x3(t)、x4(t)为正弦信号,用于模拟电机转子不平衡、机械松动等引起的低频干扰。其中,x3(t)=sin(180πt),x4(t)=sin(100πt)。仿真信号采样频率为fs=5000Hz,采样点数N=2500。选用长度为5的直线型结构元素。记冲击频率为f0(60Hz),双加性低频干扰信号频率差值为fc(40Hz)。
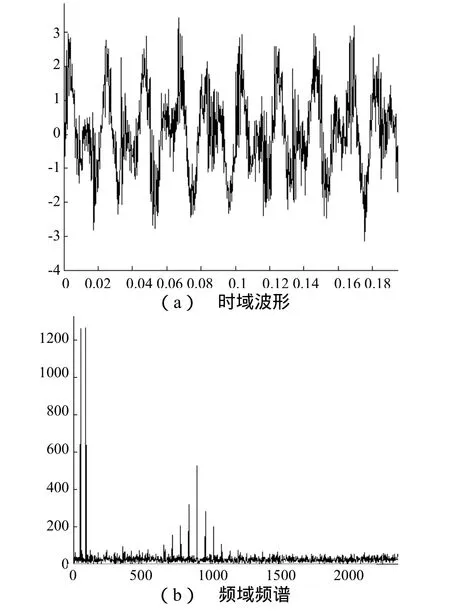
图1 仿真信号时域波形与频谱
图1 为原始信号的时域图与频谱图。由于噪声和低频信号的干扰,从图1(a)中的时域波形中较难看出周期性脉冲特性。从图1(b)中则可以清晰看出以900Hz为中心的调制频谱族与两个低频的干扰。
对仿真信号依次用形态梯度解调算子、形态差值解调算子、包络解调三种方法进行解调,结果如图2。可以看出,形态梯度算子与形态差值算子均将特征频率f0及其倍频清晰地解调出来。而图2(c)所示的包络解调则显著地将双加性低频干扰信号的频率差值fc解调出来,且其能量得到极大地增强。与此同时,特征频率f0及其倍频处频谱值则很低。这说明包络解调方法在处理具有双加性低频干扰的调制信号时具有很大的缺陷性,很容易造成误判。而形态梯度解调和形态差值解调则几乎不受双加性低频干扰的影响。
经计算,三种解调方法的低频能量比Q和特征能量比R如表1。

图2 三种解调方法对仿真信号的解调结果
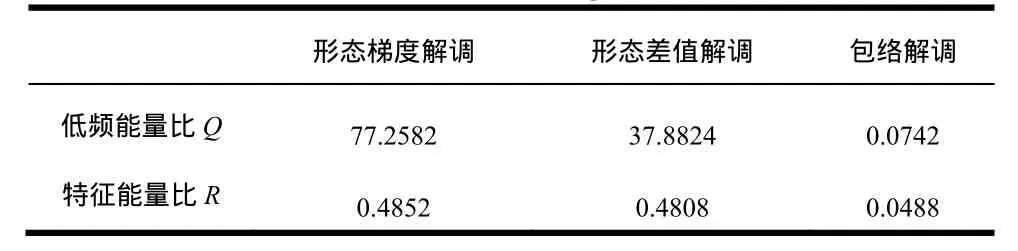
表1 三种解调方法Q、R值
由表1可以看出,当选取直线型结构长度为5时,形态梯度解调具有较高的低频能量比和特征能量比,说明运用该算子进行解调可以获得很好的抗低频干扰能力和良好的解调性能。而包络解调由于处理双加性低频干扰的局限性,因而两个参数值都很低,性能较差。另外,在特征能量比参数上,形态差值解调具有和形态梯度解调近似的参数值,而在低频能量比上则相差一倍多,说明在解调性能上,二者性能相近。而形态梯度解调对于特征频率脉冲的提取程度要大于形态差值解调,因而低频能量比要更高。由此可见,在直线结构长度为5时,形态梯度解调体现了最优的效果,形态差值解调次之,而包络解调最差。
2.2 直线型结构长度影响分析
由于本文所研究的是时间-幅值振动信号,所以采用直线型结构元素进行解调。一般而言,结构元素的选取对形态解调的效果影响极大。针对此,为更全面地比较分析形态梯度解调和形态差值解调在不同结构长度时的性能,本节针对2.2节中模拟信号分别建立了“结构长度-低频能量比”和“结构长度-特征能量比”曲线,分别如图3、4所示。
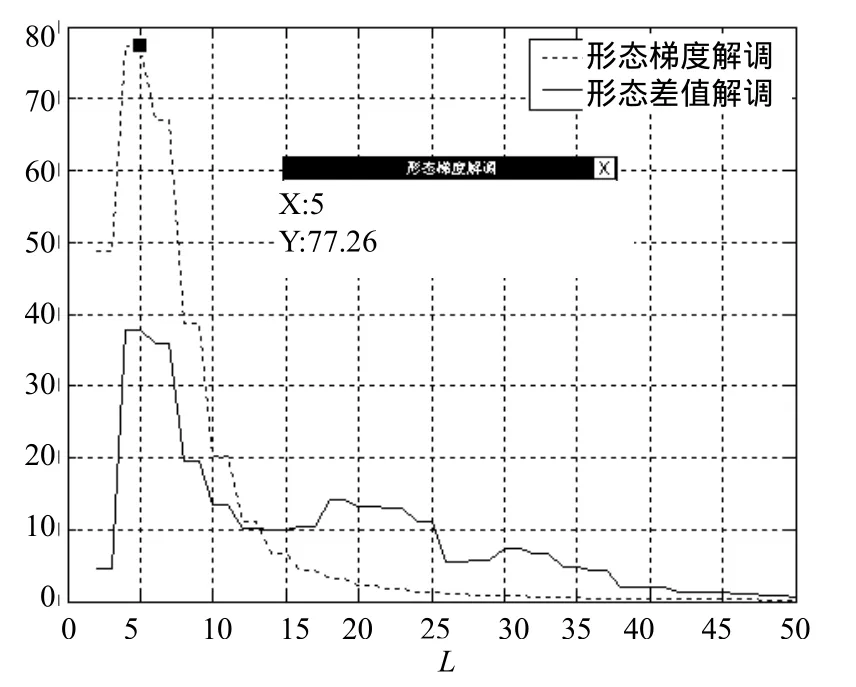
图3 直线型结构长度与低频能量比关系曲线
图3中,两种解调方法的低频能量比均在结构长度L=5时取得峰值。当0<L<5时,低频能量比呈单调递增趋势;当5<L<50时,呈递减趋势,形态差值解调在此区间段略有起伏。而两种算法的最大值在形态梯度解调曲线上取得。所以,选取结构长度为L=5的形态梯度算子进行解调,可以获得最优的抗低频干扰能力。
图4中,通过对比看出,两种解调方法的特征能量比整体趋势相近,且最大值在长度为13处的形态梯度解调曲线上取得,可见,在解调性能上,两种算法相近,形态梯度解调要略优于形态差值解调,且在长度为13时取得最优。
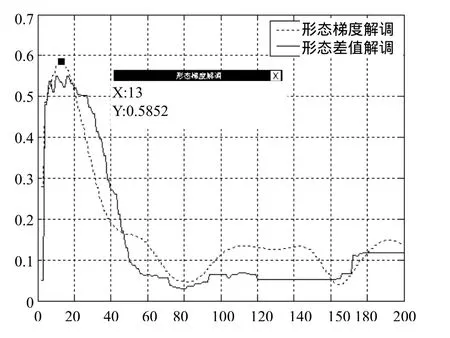
图4 直线型结构长度与特征能量比关系曲线
综上,相对于包络解调方法,数学形态解调具有抗双加性低频干扰能力强的优点。而形态梯度算子在抗双加性低频干扰的能力和解调效果均要优于形态差值解调。因此本文选用形态梯度解调方法对电机轴承故障信号进行分析。
3 实测轴承故障信号分析
为了验证本文所提出的方法的有效性,对典型的滚动轴承外圈故障进行分析。实验数据来自CWRU实验室[12]。测试轴承为SKF6205-2RS深沟球轴承,采样频率12kHz。轴承的局部损伤是由电火花机在轴承内圈人工加工制作。故障直径为0.18mm,转速1797r/min,经计算,外圈故障频率为f0=107.36Hz。
电机轴承外圈故障的时域波形与频谱如图5所示。从(a)图可以看出,轴承内圈故障信号具有明显的周期性调幅特性。而(b)图则表现出两处显著和一处微弱的调制特性频谱。其中在高频区域,分别以3445Hz和2800Hz为中心频率出现一组频率宽度约为108Hz的显著边频序列。低频区域中,以690Hz为中心频率出现一组频率宽度为30Hz的微弱边频序列。分析可知,轴承外圈故障导致产生了两处显著的调幅频谱。
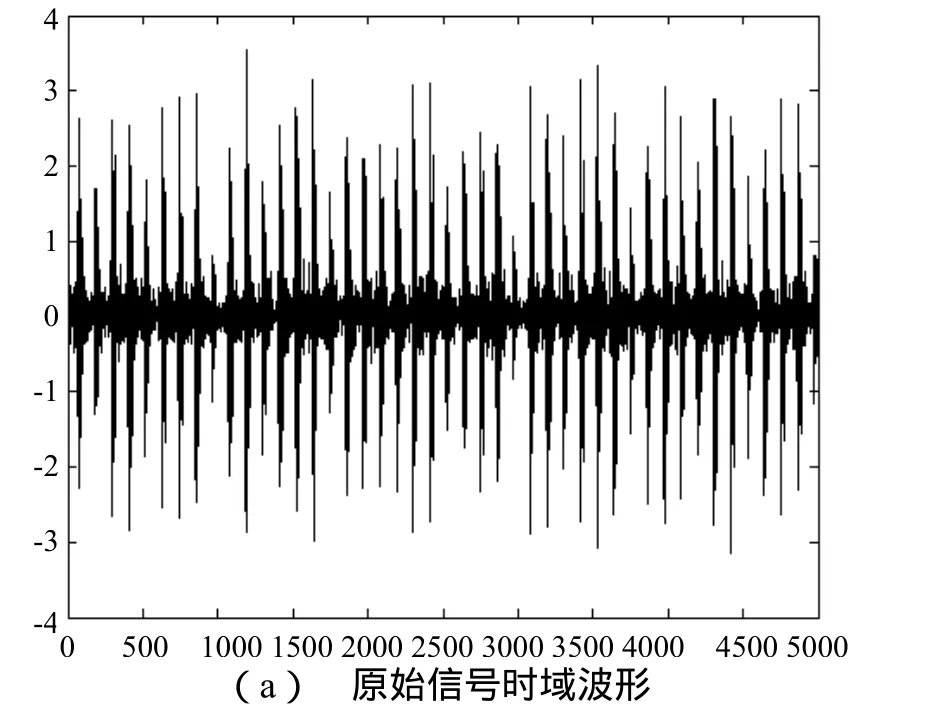
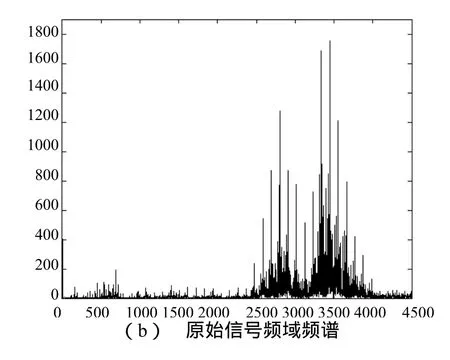
图5 轴承振动信号分析
为使形态算子解调轴承外圈故障信号达到最优,分析在固定采样频率和采样点数条件下,特征能量比R随直线型结构长度变化的趋势,如图6(a)所示。当结构长度为L=22或L=23时,特征能量比可达最大值,此时R=0.7735,解调效果达到最佳。对比图6(b)中的形态差值解调变化趋势可知,形态差值在L=15时,特征能量比达到最大值R=0.7539,解调效果略小于形态算子解调。此外,经计算,包络法用于此外圈故障信号解调时,特征能量比最大值R=0.6123。由此可见,在三种方法中,当直线型结构长度取22或23时,形态算子解调效果达到最优。

图6 “结构长度-特征能量比”
选用结构长度为23的形态梯度算子对故障信号进行解调。解调结果如图7所示。外圈故障特征频率f0(107.36Hz)及其倍频处存在明显谱线。此外在低频30Hz处也存在一处能量谱线,分析可知,正是此低频导致产生图5(b)中的轻微调制现象。
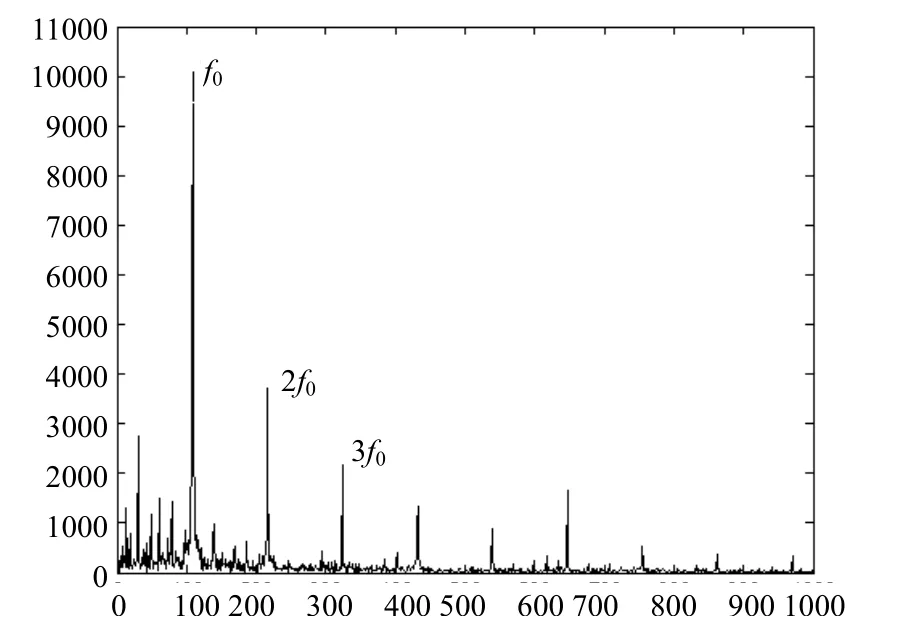
图7 形态梯度算子解调结果
4 结束语
电机轴承出现故障时,振动信号常常会混杂环境噪声和低频干扰。本文分析了数学形态学算子对信号处理的影响,对比了形态梯度解调、形态差值解调以及包络解调在处理双加性低频干扰信号时的抗噪能力和解调效果。提出用数学形态梯度算子对电机轴承故障信号进行分析和特征提取。在对实测信号的处理过程中,成功地提取出外圈故障特征频率,证明了这是一种有效的解调方法。
[1]崔玲丽, 高立新, 等. 基于第二代小波和EMD的解调方法及其应用研究[J]. 振动与冲击, 2008,27(6): 1-3.
[2]雷文平, 韩捷, 等. 小波一能量算子解调法的滚动轴承故障诊断[J]. 武汉理工大学学报. 2008,30(5): 128-131.
[3]陈泽鑫. 小波基函数在故障诊断中的最佳选择[J].机械科学与技术, 2005, 24(2): 172-176.
[4]段晨东, 何正嘉. 基于第二代小波变换的转子碰摩故障特征提取方法[J]. 汽轮机技术, 2006, 48(1):34-39.
[5]Serra J, Vincent L. An overview of morphological filtering[J]. Circuits Systems and Signal Processing,1992(11): 47-108.
[6]周川. 基于Hilbert-Huang变换的滚动轴承故障诊断方法研究[D]. 昆明: 昆明理工大学, 2010.
[7]Nikolaou N G. IAA Application of morphological operators as envelope extractors for impulsive-type periodic signals[J]. Mechanical Systems and Signal Processing, 2003(17): 1147-1162.
[8]杜秋华, 杨曙年. 形态滤波在滚动轴承缺陷诊断中的应用[J]. 轴承, 2005, 37(6): 27-31.
[9]胡爱军, 唐贵基, 安连锁. 基于数学形态学的旋转机械振动信号降噪方法[J]. 机械工程学报,2006, 42(4): 127-130.
[10]章立军, 杨德斌, 徐金梧, 等. 基于数学形态滤波的齿轮故障特征提取方法[J]. 机械工程学报,2007, 43(2): 71-75.
[11]沈路. 形态解调在齿轮故障特征提取中的应用[J]. 浙江大学学报(工学版), 2010, 44(8):1514-1519.
[12]曾庆虎. 基于小波相关滤波-包络分析的早期故障特征提取方法[J]. 仪器仪表学报, 2008, 29(4):731-732.
